
Question and Answers Forum
Question Number 36846 by Tinkutara last updated on 06/Jun/18
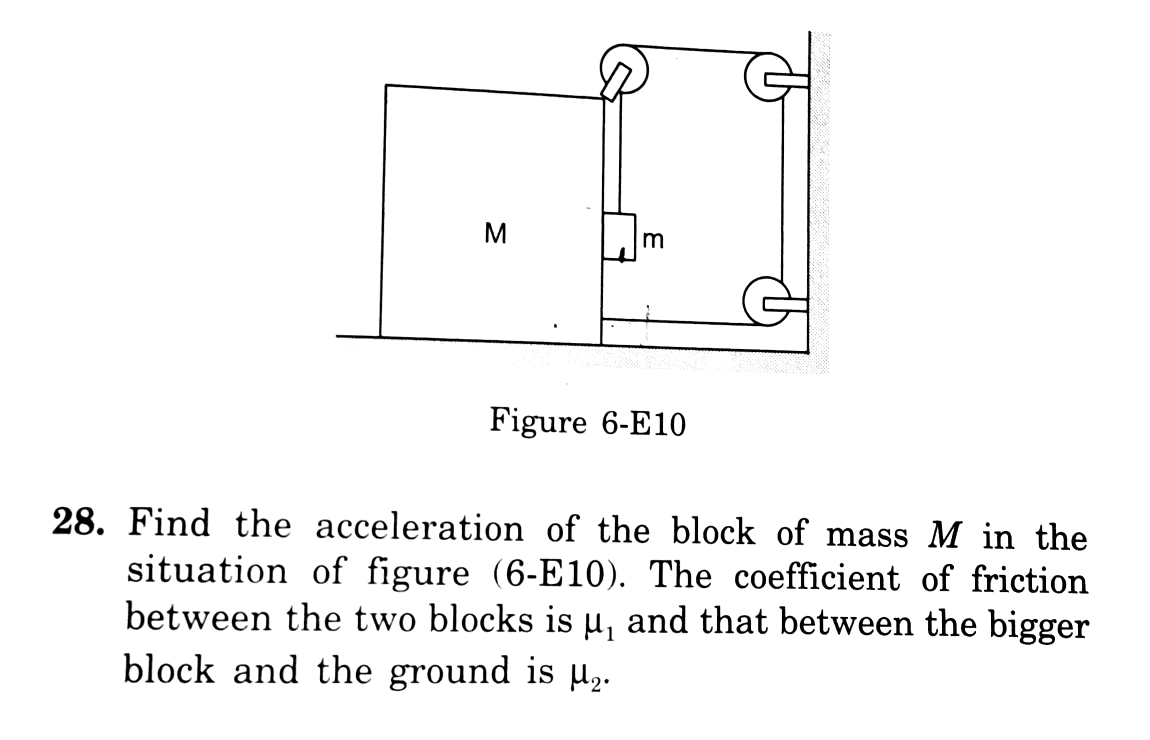
Commented by Tinkutara last updated on 08/Jun/18
?
Commented by ajfour last updated on 14/Jun/18
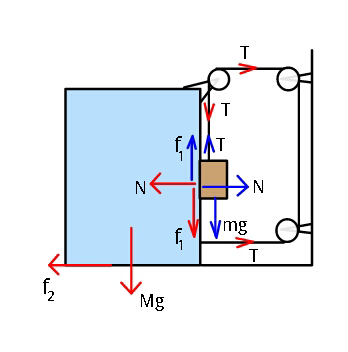
Commented by ajfour last updated on 14/Jun/18
![let A be acceleration of big block. acc. of small block a=2A for small block: mg−T−𝛍_1 N_1 =m(2A) ...(i) N_1 =mA ...(ii) ⇒ T=mg−μ_1 mA−2mA ...(iii) for larger block: N_2 =Mg+T+𝛍_1 N_1 ....(iv) 2T−N_1 −𝛍_2 N_2 = MA ...(v) using (ii) and (iv) in (v) 2T−mA−μ_2 (Mg+T+μ_1 mA)=MA using (iii) here (2−μ_2 )[mg−(2+μ_1 )mA] −(1+μ_1 μ_2 )mA−MA=μ_2 Mg ⇒ A = (([2m−𝛍_2 (M+m)]g)/(M+m[5+2(𝛍_1 −𝛍_2 )])) . ....](Q37544.png)
Commented by Tinkutara last updated on 14/Jun/18
Sir can you explain iv equation? Why T is included in FBD of M?
Commented by ajfour last updated on 14/Jun/18
small block hangs, tension in string, pulls down pulley attached to big block, pulley part of big block so tension tries sinking big block into the ground, hence appears in fbd of big block.
Commented by Tinkutara last updated on 15/Jun/18
Thank you Sir. ☺☺
Answered by MrW3 last updated on 14/Jun/18
![T=tension in string N_1 =normal force between m and M N_2 =normal force between M and ground a=acceleration of m (→) and M (→) 2a=acceleration of m (↓) mg−T−μ_1 N_1 =2ma N_1 =ma Mg+T+μ_1 N_1 −N_2 =0 2T−N_1 −μ_2 N_2 =Ma mg−T−μ_1 ma=2ma ⇒T=m(g−μ_1 a−2a) N_2 =Mg+m(g−μ_1 a−2a)+μ_1 ma ⇒N_2 =Mg+m(g−2a) 2m(g−μ_1 a−2a)−ma−μ_2 [Mg+m(g−2a)]=Ma 2mg−2μ_1 ma−5ma−Mμ_2 g−mμ_2 g+2mμ_2 a=Ma [M+(5+2μ_1 −2μ_2 )m]a=[2m−(M+m)μ_2 ]g ⇒a=(([2m−(M+m)μ_2 ]g)/(M+[5+2(μ_1 −μ_2 )]m))](Q37325.png)
Commented by Tinkutara last updated on 14/Jun/18
Sir the answer doesn't match with book.
Commented by MrW3 last updated on 14/Jun/18
Commented by Tinkutara last updated on 15/Jun/18
Thank you Sir. ����
