
Question and Answers Forum
Question Number 36853 by tawa tawa last updated on 06/Jun/18
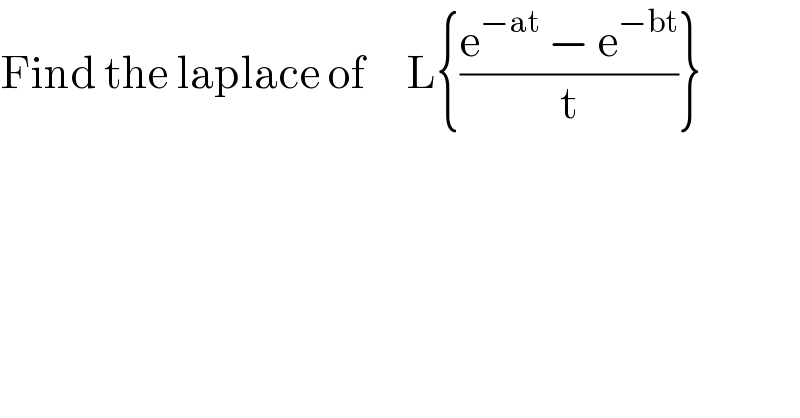
Commented by prof Abdo imad last updated on 06/Jun/18
![L{ ((e^(−ax) −e^(−bx) )/x)} =∫_0 ^∞ f(t)e^(−xt) dt ∫_0 ^∞ ((e^(−at) −e^(−bt) )/t) e^(−xt) dt =ϕ(x) so if a>0 ,b>0 we have ϕ^′ (x) = ∫_0 ^∞ (∂/∂x){ ((e^(−at) −e^(−bt) )/t) e^(−xt) }dt =−∫_0 ^∞ ( e^(−at) −e^(−bt) )e^(−xt) dt =∫_0 ^∞ (e^(−(b+x)t) −e^(−(a+x)t) )e^(−xt) dt = ∫_0 ^∞ e^(−(b+x)t) dt − ∫_0 ^∞ e^(−(a+x)t) dt =((−1)/(b+x))[ e^(−(b+x)t) ]_(t=0) ^∞ +(1/(a+x))[ e^(−(a+x)t) ]_(t=0) ^∞ = (1/(b+x)) −(1/(a+x)) ⇒ϕ(x)= ln∣b+x∣−ln∣a+x∣ +c =ln∣ ((b+x)/(a+x))∣ +c but c=lim_(x→+∞) {ϕ(x)−ln(((b+x)/(a+x)))} ∃m>0 / ∣ϕ(x)∣<m ∫_0 ^∞ e^(−xt) d t =(m/x) →0(x→+∞) ⇒c =0 and ϕ(x)=ln (((b+x)/(a+x))) .](Q36889.png)
Commented by tawa tawa last updated on 06/Jun/18
| ||
Question and Answers Forum | ||
Question Number 36853 by tawa tawa last updated on 06/Jun/18 | ||
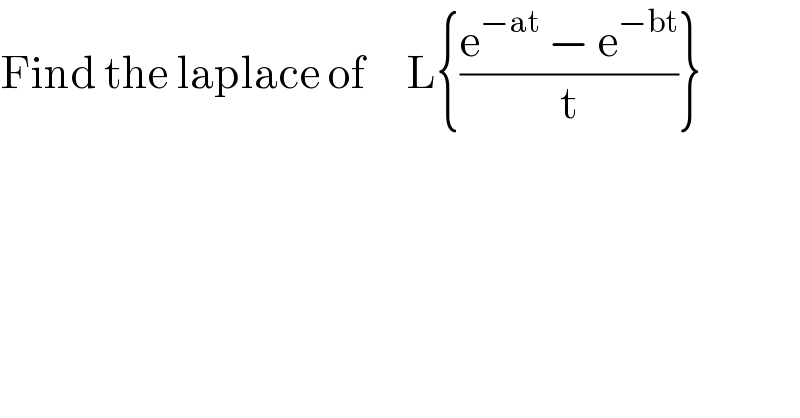 | ||
Commented by prof Abdo imad last updated on 06/Jun/18 | ||
![L{ ((e^(−ax) −e^(−bx) )/x)} =∫_0 ^∞ f(t)e^(−xt) dt ∫_0 ^∞ ((e^(−at) −e^(−bt) )/t) e^(−xt) dt =ϕ(x) so if a>0 ,b>0 we have ϕ^′ (x) = ∫_0 ^∞ (∂/∂x){ ((e^(−at) −e^(−bt) )/t) e^(−xt) }dt =−∫_0 ^∞ ( e^(−at) −e^(−bt) )e^(−xt) dt =∫_0 ^∞ (e^(−(b+x)t) −e^(−(a+x)t) )e^(−xt) dt = ∫_0 ^∞ e^(−(b+x)t) dt − ∫_0 ^∞ e^(−(a+x)t) dt =((−1)/(b+x))[ e^(−(b+x)t) ]_(t=0) ^∞ +(1/(a+x))[ e^(−(a+x)t) ]_(t=0) ^∞ = (1/(b+x)) −(1/(a+x)) ⇒ϕ(x)= ln∣b+x∣−ln∣a+x∣ +c =ln∣ ((b+x)/(a+x))∣ +c but c=lim_(x→+∞) {ϕ(x)−ln(((b+x)/(a+x)))} ∃m>0 / ∣ϕ(x)∣<m ∫_0 ^∞ e^(−xt) d t =(m/x) →0(x→+∞) ⇒c =0 and ϕ(x)=ln (((b+x)/(a+x))) .](Q36889.png) | ||
Commented by tawa tawa last updated on 06/Jun/18 | ||
 | ||