Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 36923 by maxmathsup by imad last updated on 07/Jun/18

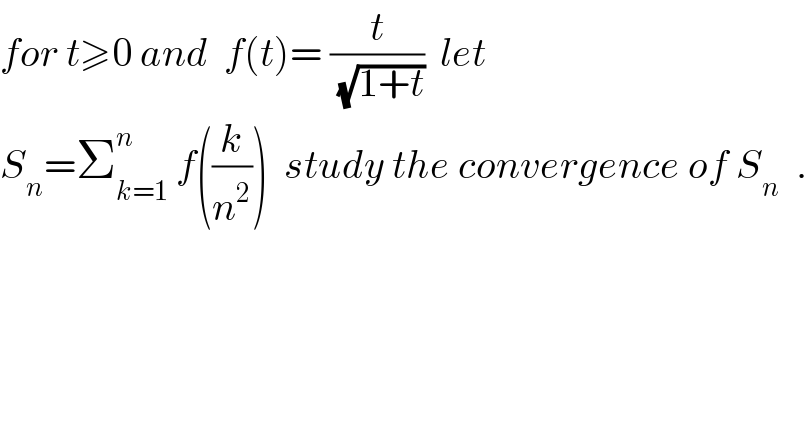
for t≥0 and f(t)= (t/(√(1+t))) let S_n =Σ_(k=1) ^n f((k/n^2 )) study the convergence of S_n .

$${for}\:{t}\geqslant\mathrm{0}\:{and}\:\:{f}\left({t}\right)=\:\frac{{t}}{\sqrt{\mathrm{1}+{t}}}\:\:{let} \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:{f}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right)\:\:{study}\:{the}\:{convergence}\:{of}\:{S}_{{n}} \:\:. \\ $$

Commented by abdo.msup.com last updated on 10/Jun/18

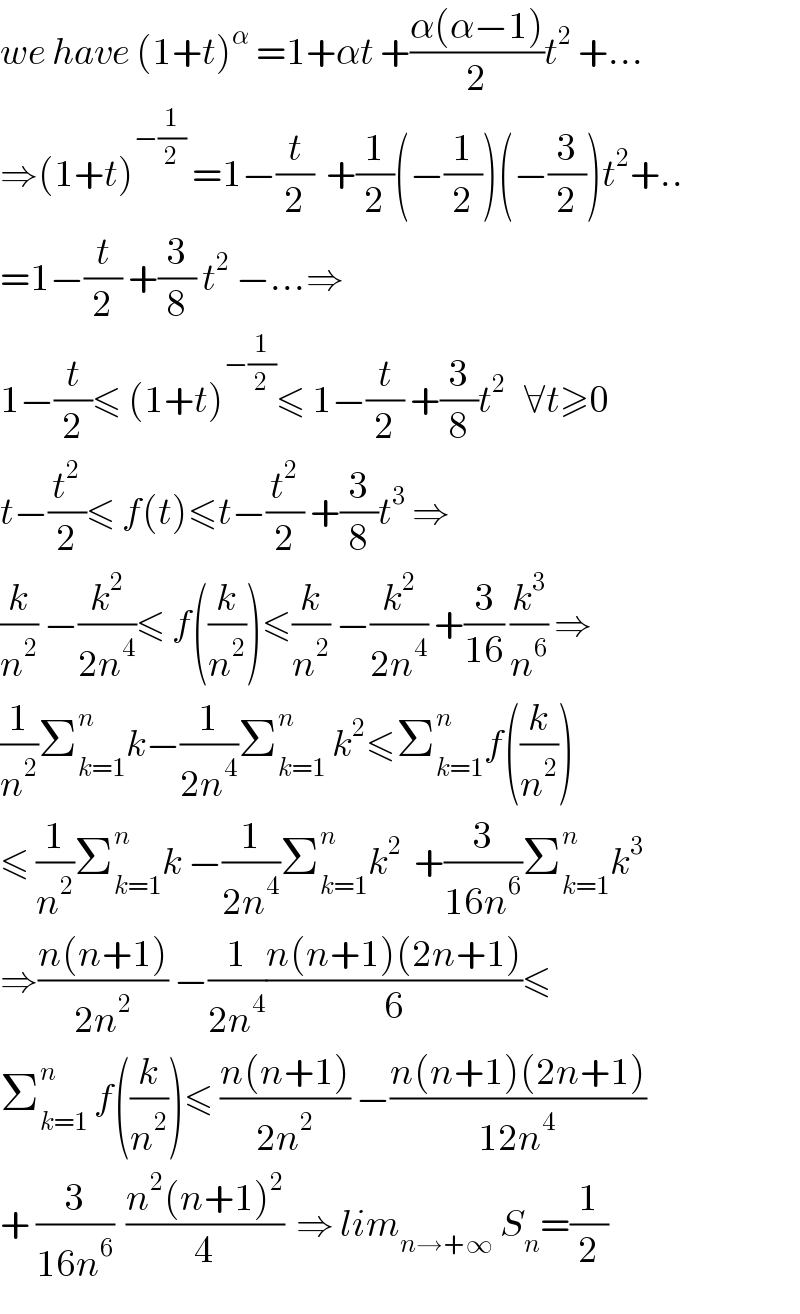
we have (1+t)^α =1+αt +((α(α−1))/2)t^2 +... ⇒(1+t)^(−(1/2)) =1−(t/2) +(1/2)(−(1/2))(−(3/2))t^2 +.. =1−(t/2) +(3/8) t^2 −...⇒ 1−(t/2)≤ (1+t)^(−(1/2)) ≤ 1−(t/2) +(3/8)t^2 ∀t≥0 t−(t^2 /2)≤ f(t)≤t−(t^2 /2) +(3/8)t^3 ⇒ (k/n^2 ) −(k^2 /(2n^4 ))≤ f((k/n^2 ))≤(k/n^2 ) −(k^2 /(2n^4 )) +(3/(16)) (k^3 /n^6 ) ⇒ (1/n^2 )Σ_(k=1) ^n k−(1/(2n^4 ))Σ_(k=1) ^n k^2 ≤Σ_(k=1) ^n f((k/n^2 )) ≤ (1/n^2 )Σ_(k=1) ^n k −(1/(2n^4 ))Σ_(k=1) ^n k^2 +(3/(16n^6 ))Σ_(k=1) ^n k^3 ⇒((n(n+1))/(2n^2 )) −(1/(2n^4 ))((n(n+1)(2n+1))/6)≤ Σ_(k=1) ^n f((k/n^2 ))≤ ((n(n+1))/(2n^2 )) −((n(n+1)(2n+1))/(12n^4 )) + (3/(16n^6 )) ((n^2 (n+1)^2 )/4) ⇒ lim_(n→+∞) S_n =(1/2)

$${we}\:{have}\:\left(\mathrm{1}+{t}\right)^{\alpha} \:=\mathrm{1}+\alpha{t}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} \:+... \\ $$$$\Rightarrow\left(\mathrm{1}+{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}−\frac{{t}}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right){t}^{\mathrm{2}} +.. \\ $$$$=\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{8}}\:{t}^{\mathrm{2}} \:−...\Rightarrow \\ $$$$\mathrm{1}−\frac{{t}}{\mathrm{2}}\leqslant\:\left(\mathrm{1}+{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \leqslant\:\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{8}}{t}^{\mathrm{2}} \:\:\:\forall{t}\geqslant\mathrm{0} \\ $$$${t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\leqslant\:{f}\left({t}\right)\leqslant{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{8}}{t}^{\mathrm{3}} \:\Rightarrow \\ $$$$\frac{{k}}{{n}^{\mathrm{2}} }\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\leqslant\:{f}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\frac{{k}}{{n}^{\mathrm{2}} }\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:+\frac{\mathrm{3}}{\mathrm{16}}\:\frac{{k}^{\mathrm{3}} }{{n}^{\mathrm{6}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \leqslant\sum_{{k}=\mathrm{1}} ^{{n}} {f}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\leqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \:\:+\frac{\mathrm{3}}{\mathrm{16}{n}^{\mathrm{6}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{3}} \\ $$$$\Rightarrow\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\leqslant \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{f}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:−\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{4}} } \\ $$$$+\:\frac{\mathrm{3}}{\mathrm{16}{n}^{\mathrm{6}} }\:\:\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\:\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com