Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 36926 by maxmathsup by imad last updated on 07/Jun/18

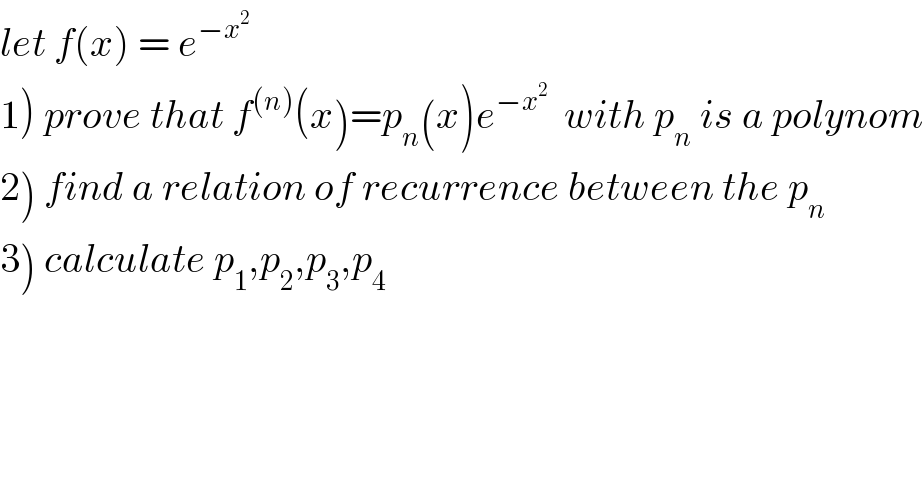
let f(x) = e^(−x^2 ) 1) prove that f^((n)) (x)=p_n (x)e^(−x^2 ) with p_n is a polynom 2) find a relation of recurrence between the p_n 3) calculate p_1 ,p_2 ,p_3 ,p_4

$${let}\:{f}\left({x}\right)\:=\:{e}^{−{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:{f}^{\left({n}\right)} \left({x}\right)={p}_{{n}} \left({x}\right){e}^{−{x}^{\mathrm{2}} } \:\:{with}\:{p}_{{n}} \:{is}\:{a}\:{polynom} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{relation}\:{of}\:{recurrence}\:{between}\:{the}\:{p}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:{p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,{p}_{\mathrm{3}} ,{p}_{\mathrm{4}} \\ $$

Answered by math khazana by abdo last updated on 10/Jun/18

we have f^′ (x) =−2x e^(−x^2 ) f^((2)) (x) =−2 e^(−x^2 ) +4x^2 e^(−x^2 ) =(4x^2 −2)e^(−x^2 ) let suppose that f^((n)) (x) =p_n (x) e^(−x^2 ) with p_n a polynome ⇒ f^((n+1)) (x)= (p_n (x)e^(−x^2 ) )^′ =p_n ^′ (x) e^(−x^2 ) −2x p_n (x) e^(−x^2 ) ={ p_n ^′ (x) −2x p_n (x)}e^(−x^2 ) =p_(n+1) (x)e^(−x^2 ) with p_(n+1) (x)= p_n ^′ (x) −2x p_n (x) and its clear that deg(p_n ) =n 2) p_(n+1) (x)= −2xp_n (x) +p_n ^′ (x) 3) p_1 (x) =−2x and p_2 (x) =−2xp_1 (x) +p_1 ^′ (x) =4x^2 −2 p_3 (x) =−2xp_2 (x) +p_2 ^′ (x) =−2x(4x^2 −2) +8x=−8x^3 +4x +8x =−8x^3 +12x p_4 (x) =−2xp_3 (x) +p_3 ^′ (x) =−2x(−8x^3 +12x) −24x^2 +12 =16 x^4 −24x^2 −24x^2 +12 =16 x^4 −48x^2 +12 .

$${we}\:{have}\:{f}^{'} \left({x}\right)\:=−\mathrm{2}{x}\:{e}^{−{x}^{\mathrm{2}} } \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)\:=−\mathrm{2}\:{e}^{−{x}^{\mathrm{2}} } \:+\mathrm{4}{x}^{\mathrm{2}} \:{e}^{−{x}^{\mathrm{2}} } \:=\left(\mathrm{4}{x}^{\mathrm{2}} \:−\mathrm{2}\right){e}^{−{x}^{\mathrm{2}} } \\ $$$${let}\:{suppose}\:{that}\:{f}^{\left({n}\right)} \left({x}\right)\:={p}_{{n}} \left({x}\right)\:{e}^{−{x}^{\mathrm{2}} } \:{with}\:{p}_{{n}} \\ $$$${a}\:{polynome}\:\Rightarrow\:{f}^{\left({n}+\mathrm{1}\right)} \left({x}\right)=\:\left({p}_{{n}} \left({x}\right){e}^{−{x}^{\mathrm{2}} } \right)^{'} \\ $$$$={p}_{{n}} ^{'} \left({x}\right)\:{e}^{−{x}^{\mathrm{2}} } \:−\mathrm{2}{x}\:{p}_{{n}} \left({x}\right)\:{e}^{−{x}^{\mathrm{2}} } \\ $$$$=\left\{\:{p}_{{n}} ^{'} \left({x}\right)\:−\mathrm{2}{x}\:{p}_{{n}} \left({x}\right)\right\}{e}^{−{x}^{\mathrm{2}} \:} \:\:\:={p}_{{n}+\mathrm{1}} \:\left({x}\right){e}^{−{x}^{\mathrm{2}} } \\ $$$${with}\:\:{p}_{{n}+\mathrm{1}} \left({x}\right)=\:{p}_{{n}} ^{'} \left({x}\right)\:−\mathrm{2}{x}\:{p}_{{n}} \left({x}\right)\:{and}\:{its}\:{clear} \\ $$$${that}\:{deg}\left({p}_{{n}} \right)\:={n} \\ $$$$\left.\mathrm{2}\right)\:{p}_{{n}+\mathrm{1}} \left({x}\right)=\:−\mathrm{2}{xp}_{{n}} \left({x}\right)\:+{p}_{{n}} ^{'} \left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:{p}_{\mathrm{1}} \left({x}\right)\:=−\mathrm{2}{x}\:\:{and}\:{p}_{\mathrm{2}} \left({x}\right)\:=−\mathrm{2}{xp}_{\mathrm{1}} \left({x}\right)\:+{p}_{\mathrm{1}} ^{'} \left({x}\right) \\ $$$$=\mathrm{4}{x}^{\mathrm{2}} \:−\mathrm{2} \\ $$$${p}_{\mathrm{3}} \left({x}\right)\:=−\mathrm{2}{xp}_{\mathrm{2}} \left({x}\right)\:+{p}_{\mathrm{2}} ^{'} \left({x}\right)\: \\ $$$$=−\mathrm{2}{x}\left(\mathrm{4}{x}^{\mathrm{2}} \:−\mathrm{2}\right)\:+\mathrm{8}{x}=−\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{4}{x}\:+\mathrm{8}{x} \\ $$$$=−\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{12}{x} \\ $$$${p}_{\mathrm{4}} \left({x}\right)\:=−\mathrm{2}{xp}_{\mathrm{3}} \left({x}\right)\:+{p}_{\mathrm{3}} ^{'} \left({x}\right) \\ $$$$=−\mathrm{2}{x}\left(−\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{12}{x}\right)\:−\mathrm{24}{x}^{\mathrm{2}} \:+\mathrm{12} \\ $$$$=\mathrm{16}\:{x}^{\mathrm{4}} \:\:−\mathrm{24}{x}^{\mathrm{2}} \:−\mathrm{24}{x}^{\mathrm{2}} \:+\mathrm{12} \\ $$$$=\mathrm{16}\:{x}^{\mathrm{4}} \:−\mathrm{48}{x}^{\mathrm{2}} \:+\mathrm{12}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com