
Question and Answers Forum
Question Number 36940 by maxmathsup by imad last updated on 07/Jun/18
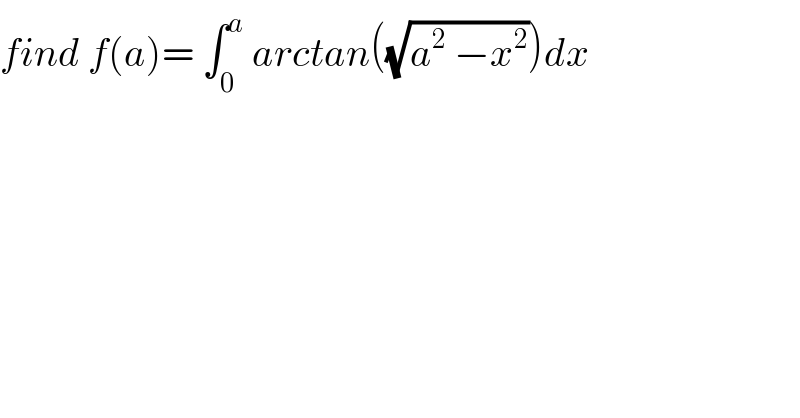
Commented by math khazana by abdo last updated on 08/Jun/18
![changement (√(a^2 −x^2 ))=t givea^2 −x^2 =t^2 ⇒ x^2 =a^2 −t^2 ⇒x=(√(a^2 −t^2 ))⇒dx = ((−2tdt)/(2(√(a^2 −t^2 )))) f(a) = ∫_0 ^a arctan(t) ((t dt)/(√(a^2 −t^2 ))) by parts f(a) =[−arctan(t)(√(a^2 −t^2 ))]_0 ^a −∫_0 ^a ((−(√(a^2 −t^2 )))/(1+t^2 )) dt = ∫_0 ^a ((√(a^2 −t^2 ))/(1+t^2 )) dt changement t= a sinα give f(a) = ∫_0 ^(π/2) ((∣a∣cosα)/(1+a^2 sin^2 α)) acosα dα =a∣a∣ ∫_0 ^(π/2) ((cos^2 α)/(1+a^2 sin^2 α))dα but ((cos^2 α)/(1+a^2 sin^2 α)) = ((1/(1+tan^2 α))/(1+a^2 (1−(1/(1+tan^2 α))))) = (1/((1+tan^2 α)(1+a^2 tan^2 α).(1/(1+tan^2 α)))) = (1/(1 +a^2 tan^2 α)) ⇒ f(a)=a∣a∣ ∫_0 ^(π/2) (dα/(1+a^2 tan^2 α)) =_(atan(α)=x) a∣a∣ ∫_0 ^(+∞) (1/(1+x^2 )) (1/(a( 1+(x^2 /a^2 ))))dx =∣a∣ ∫_0 ^∞ ((a^2 dx)/((1+x^2 )( x^2 +a^2 ))) case1 a>0 anda≠1⇒f(a) =(a^3 /2) ∫_(−∞) ^(+∞) (dx/((x^2 +1)(x^2 +a^2 ))) let ϕ(z) = (1/((z^2 +1)(z^2 +a^2 ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,i)+Res(ϕ,ia)} ϕ(z)= (1/((z−i)(z+i)(z−ia)(z+ia))) Res(ϕ,i)= (1/(2i(a^2 −1))) Res(ϕ^� ,ia) = (1/(2ia(1−a^2 ))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(2i(a^2 −1))) +(1/(2ia(1−a^2 )))} =(π/(a^2 −1)){ 1−(1/a)}= ((π(a−1))/(a(a^2 −1))) =(π/(a(a+1))) f(a)= (a^3 /2) .(π/(a(a+1))) = ((πa^2 )/(2(a+1))) case 2 a<0 and a≠−1 we folow the same method...](Q37083.png)
| ||
Question and Answers Forum | ||
Question Number 36940 by maxmathsup by imad last updated on 07/Jun/18 | ||
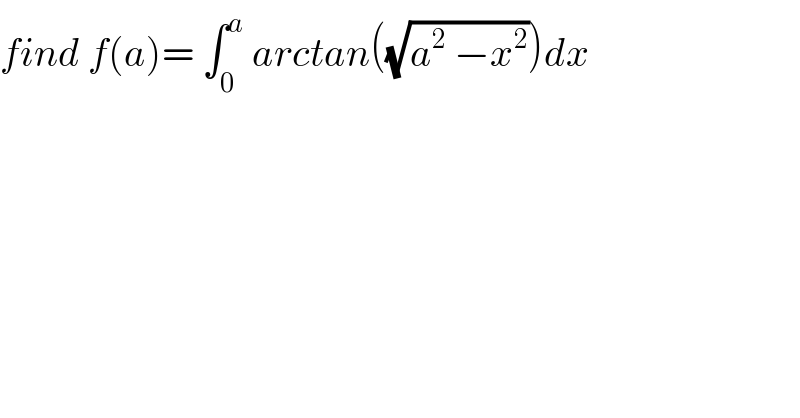 | ||
Commented by math khazana by abdo last updated on 08/Jun/18 | ||
![changement (√(a^2 −x^2 ))=t givea^2 −x^2 =t^2 ⇒ x^2 =a^2 −t^2 ⇒x=(√(a^2 −t^2 ))⇒dx = ((−2tdt)/(2(√(a^2 −t^2 )))) f(a) = ∫_0 ^a arctan(t) ((t dt)/(√(a^2 −t^2 ))) by parts f(a) =[−arctan(t)(√(a^2 −t^2 ))]_0 ^a −∫_0 ^a ((−(√(a^2 −t^2 )))/(1+t^2 )) dt = ∫_0 ^a ((√(a^2 −t^2 ))/(1+t^2 )) dt changement t= a sinα give f(a) = ∫_0 ^(π/2) ((∣a∣cosα)/(1+a^2 sin^2 α)) acosα dα =a∣a∣ ∫_0 ^(π/2) ((cos^2 α)/(1+a^2 sin^2 α))dα but ((cos^2 α)/(1+a^2 sin^2 α)) = ((1/(1+tan^2 α))/(1+a^2 (1−(1/(1+tan^2 α))))) = (1/((1+tan^2 α)(1+a^2 tan^2 α).(1/(1+tan^2 α)))) = (1/(1 +a^2 tan^2 α)) ⇒ f(a)=a∣a∣ ∫_0 ^(π/2) (dα/(1+a^2 tan^2 α)) =_(atan(α)=x) a∣a∣ ∫_0 ^(+∞) (1/(1+x^2 )) (1/(a( 1+(x^2 /a^2 ))))dx =∣a∣ ∫_0 ^∞ ((a^2 dx)/((1+x^2 )( x^2 +a^2 ))) case1 a>0 anda≠1⇒f(a) =(a^3 /2) ∫_(−∞) ^(+∞) (dx/((x^2 +1)(x^2 +a^2 ))) let ϕ(z) = (1/((z^2 +1)(z^2 +a^2 ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,i)+Res(ϕ,ia)} ϕ(z)= (1/((z−i)(z+i)(z−ia)(z+ia))) Res(ϕ,i)= (1/(2i(a^2 −1))) Res(ϕ^� ,ia) = (1/(2ia(1−a^2 ))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(2i(a^2 −1))) +(1/(2ia(1−a^2 )))} =(π/(a^2 −1)){ 1−(1/a)}= ((π(a−1))/(a(a^2 −1))) =(π/(a(a+1))) f(a)= (a^3 /2) .(π/(a(a+1))) = ((πa^2 )/(2(a+1))) case 2 a<0 and a≠−1 we folow the same method...](Q37083.png) | ||