Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 3695 by Rasheed Soomro last updated on 19/Dec/15

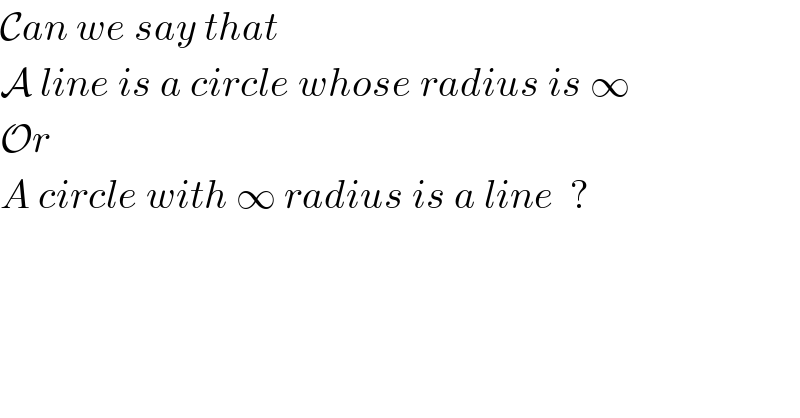
Can we say that A line is a circle whose radius is ∞ Or A circle with ∞ radius is a line ?

$$\mathcal{C}{an}\:{we}\:{say}\:{that} \\ $$$$\mathcal{A}\:{line}\:{is}\:{a}\:{circle}\:{whose}\:{radius}\:{is}\:\infty \\ $$$$\mathcal{O}{r} \\ $$$${A}\:{circle}\:{with}\:\infty\:{radius}\:{is}\:{a}\:{line}\:\:? \\ $$

Commented by Filup last updated on 19/Dec/15

A line l^→ =∞ is like a vector l^→ moves in one direction (1D). l^→ ∈R^1 A circle with radus r^→ =∞is similar. Except a circle will eventually create tangents facing every possible direction in what we can call a 2D plane. r^→ ∈R^2 This is just what i think. I could be wrong.

$${A}\:\mathrm{line}\:\overset{\rightarrow} {{l}}=\infty\:\mathrm{is}\:\mathrm{like}\:\mathrm{a}\:\mathrm{vector} \\ $$$$\overset{\rightarrow} {{l}}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{one}\:\mathrm{direction}\:\left(\mathrm{1D}\right). \\ $$$$\overset{\rightarrow} {{l}}\in\mathbb{R}^{\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{A}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{radus}\:\overset{\rightarrow} {{r}}=\infty\mathrm{is}\:\mathrm{similar}. \\ $$$$\mathrm{Except}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{will}\:\mathrm{eventually}\:\mathrm{create} \\ $$$$\mathrm{tangents}\:\mathrm{facing}\:\mathrm{every}\:\mathrm{possible}\:\mathrm{direction} \\ $$$$\mathrm{in}\:\mathrm{what}\:\mathrm{we}\:\mathrm{can}\:\mathrm{call}\:\mathrm{a}\:\mathrm{2D}\:\mathrm{plane}. \\ $$$$\overset{\rightarrow} {{r}}\in\mathbb{R}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{just}\:\mathrm{what}\:\mathrm{i}\:\mathrm{think}.\:\mathrm{I}\:\mathrm{could}\:\mathrm{be} \\ $$$$\mathrm{wrong}. \\ $$

Commented by Filup last updated on 19/Dec/15

Actually, a correction i want to point out. r^→ ∉R^2 the circle c^→ ∈R^2 . The radius is 1D. r^→ ∈R^1 A line only has one feature: its length l^→ ∈R^1 A circle (c^→ ) has two features. The radius and the circumference. r^→ ∈R^1 c^→ ∈R^2 The circle itself lies within a 2D plane. The radius is in a 1D plane

$${A}\mathrm{ctually},\:{a}\:{correction}\:{i}\:{want}\:{to}\:{point}\:{out}. \\ $$$$ \\ $$$$\overset{\rightarrow} {{r}}\notin\mathbb{R}^{\mathrm{2}} \\ $$$${the}\:\mathrm{circle}\:\overset{\rightarrow} {{c}}\in\mathbb{R}^{\mathrm{2}} . \\ $$$$\mathrm{The}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{1D}.\:\overset{\rightarrow} {{r}}\in\mathbb{R}^{\mathrm{1}} \\ $$$$ \\ $$$${A}\:\mathrm{line}\:\mathrm{only}\:\mathrm{has}\:\mathrm{one}\:\mathrm{feature}: \\ $$$$\mathrm{its}\:\mathrm{length}\:\overset{\rightarrow} {{l}}\in\mathbb{R}^{\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{A}\:\mathrm{circle}\:\left(\overset{\rightarrow} {{c}}\right)\:\mathrm{has}\:\mathrm{two}\:\mathrm{features}. \\ $$$$\mathrm{The}\:\mathrm{radius}\:\mathrm{and}\:\mathrm{the}\:\mathrm{circumference}. \\ $$$$\overset{\rightarrow} {{r}}\in\mathbb{R}^{\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\:\overset{\rightarrow} {{c}}\in\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{circle}\:\mathrm{itself}\:\mathrm{lies}\:\mathrm{within}\:\mathrm{a}\:\mathrm{2D}\:\mathrm{plane}. \\ $$$$\mathrm{The}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{in}\:\mathrm{a}\:\mathrm{1D}\:\mathrm{plane} \\ $$

Commented by RasheedSindhi last updated on 19/Dec/15

Perhaps I can′t clear what I mean. If an object revolves on a circular path, the object is said to be contineously changing direction. Consider my ′change of direction′ somewhat like that. Consider a circle path of moving point which keeps changing direction at every position.

$${Perhaps}\:{I}\:{can}'{t}\:{clear}\:{what}\:{I}\:{mean}. \\ $$$$\mathcal{I}{f}\:{an}\:{object}\:{revolves}\:{on}\:{a}\:{circular} \\ $$$${path},\:{the}\:{object}\:{is}\:{said}\:{to}\:{be}\:\: \\ $$$${contineously}\:{changing}\:{direction}. \\ $$$${Consider}\:{my}\:'{change}\:{of}\:{direction}' \\ $$$${somewhat}\:{like}\:{that}. \\ $$$${Consider}\:{a}\:{circle}\:{path}\:{of}\:{moving} \\ $$$${point}\:{which}\:{keeps}\:{changing} \\ $$$${direction}\:{at}\:{every}\:{position}. \\ $$

Commented by prakash jain last updated on 19/Dec/15

Infinite radius means r→∞. What is the area of line? If circle is treated as line.

$$\mathrm{Infinite}\:\mathrm{radius}\:\mathrm{means}\:{r}\rightarrow\infty. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{line}?\:\mathrm{If}\:\mathrm{circle}\:\mathrm{is} \\ $$$$\mathrm{treated}\:\mathrm{as}\:\mathrm{line}. \\ $$

Commented by Rasheed Soomro last updated on 19/Dec/15

Area of line (which is considered as circle) is half plane. Half plane in which centre occurs may be considered as interior of the ′circle′ and the other half plane is exterior and length of line (of course ∞) as perimeter. When I consider a circle of ∞ radius I see a line! Its change of direction is 0 .As r gets greater, change of direction of circle gets smaller and smaller.

$${Area}\:{of}\:{line}\:\left({which}\:{is}\:{considered}\:{as}\:{circle}\right)\:{is} \\ $$$$\boldsymbol{\mathrm{half}}\:\boldsymbol{\mathrm{plane}}.\:{Half}\:{plane}\:{in}\:{which}\:{centre}\:{occurs} \\ $$$${may}\:{be}\:{considered}\:{as}\:\boldsymbol{\mathrm{interior}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:'\boldsymbol{\mathrm{circle}}' \\ $$$${and}\:{the}\:{other}\:{half}\:{plane}\:{is}\:\boldsymbol{\mathrm{exterior}}\:{and}\:{length} \\ $$$${of}\:{line}\:\left({of}\:{course}\:\infty\right)\:{as}\:\boldsymbol{\mathrm{perimeter}}. \\ $$$$ \\ $$$$\mathcal{W}{hen}\:\mathcal{I}\:{consider}\:{a}\:{circle}\:{of}\:\infty\:{radius}\:\mathcal{I}\:{see}\:{a}\:{line}! \\ $$$$\mathcal{I}{ts}\:{change}\:{of}\:{direction}\:{is}\:\mathrm{0}\:.\mathcal{A}{s}\:{r}\:{gets}\:{greater},\:{change} \\ $$$${of}\:{direction}\:{of}\:{circle}\:{gets}\:{smaller}\:{and}\:{smaller}. \\ $$

Commented by prakash jain last updated on 19/Dec/15

If by change of direction you mean angle toward the center=((arc length)/(radius)) So total =(L/r)=2π and it is independent of radius r→∞, Total change of direction is still 2π

$$\mathrm{If}\:\mathrm{by}\:\mathrm{change}\:\mathrm{of}\:\mathrm{direction}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{angle} \\ $$$$\mathrm{toward}\:\mathrm{the}\:\mathrm{center}=\frac{\mathrm{arc}\:\mathrm{length}}{\mathrm{radius}} \\ $$$$\mathrm{So}\:\mathrm{total}\:=\frac{\mathrm{L}}{{r}}=\mathrm{2}\pi\:\mathrm{and}\:\mathrm{it}\:\mathrm{is}\:\mathrm{independent}\:\mathrm{of}\:\mathrm{radius} \\ $$$${r}\rightarrow\infty,\:\mathrm{Total}\:\mathrm{change}\:\mathrm{of}\:\mathrm{direction}\:\mathrm{is}\:\mathrm{still}\:\mathrm{2}\pi \\ $$

Commented by RasheedSindhi last updated on 19/Dec/15

By change of direction I mean change of angle of tangents. Let the center of the circle is origin of the plane and the point of x−axis through which the circle passes is point A. At A the tangent is perpendicular to the x−axis.Let B is an other point of circle. Tangent on B will make angle (say) θ with x−axis. I mean by ′change of direction′ was keeping change of the value of θ.

$${By}\:{change}\:{of}\:{direction}\:{I}\:{mean} \\ $$$${change}\:{of}\:{angle}\:{of}\:{tangents}. \\ $$$${Let}\:{the}\:{center}\:{of}\:{the}\:\:{circle}\:{is} \\ $$$${origin}\:{of}\:{the}\:{plane}\:{and}\:{the}\:{point} \\ $$$${of}\:{x}−{axis}\:{through}\:{which}\:{the} \\ $$$${circle}\:{passes}\:{is}\:{point}\:{A}. \\ $$$${At}\:{A}\:{the}\:{tangent}\:{is}\:{perpendicular} \\ $$$${to}\:{the}\:{x}−{axis}.{Let}\:{B}\:{is}\:{an}\:{other} \\ $$$${point}\:{of}\:{circle}.\:{Tangent}\:{on}\:{B} \\ $$$${will}\:{make}\:{angle}\:\left({say}\right)\:\theta\:{with} \\ $$$${x}−{axis}.\:{I}\:{mean}\:\:{by}\:'{change}\:{of} \\ $$$${direction}'\:{was}\:{keeping}\:{change}\:{of}\:{the} \\ $$$${value}\:{of}\:\theta. \\ $$

Commented by prakash jain last updated on 19/Dec/15

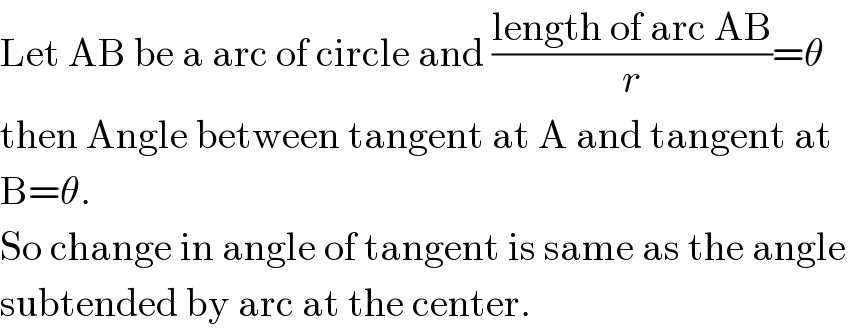
Let AB be a arc of circle and ((length of arc AB)/r)=θ then Angle between tangent at A and tangent at B=θ. So change in angle of tangent is same as the angle subtended by arc at the center.

$$\mathrm{Let}\:\mathrm{AB}\:\mathrm{be}\:\mathrm{a}\:\mathrm{arc}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{and}\:\frac{\mathrm{length}\:\mathrm{of}\:\mathrm{arc}\:\mathrm{AB}}{{r}}=\theta \\ $$$$\mathrm{then}\:\mathrm{Angle}\:\mathrm{between}\:\mathrm{tangent}\:\mathrm{at}\:\mathrm{A}\:\mathrm{and}\:\mathrm{tangent}\:\mathrm{at} \\ $$$$\mathrm{B}=\theta. \\ $$$$\mathrm{So}\:\mathrm{change}\:\mathrm{in}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{tangent}\:\mathrm{is}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{angle}\: \\ $$$$\mathrm{subtended}\:\mathrm{by}\:\mathrm{arc}\:\mathrm{at}\:\mathrm{the}\:\mathrm{center}. \\ $$

Commented by prakash jain last updated on 19/Dec/15

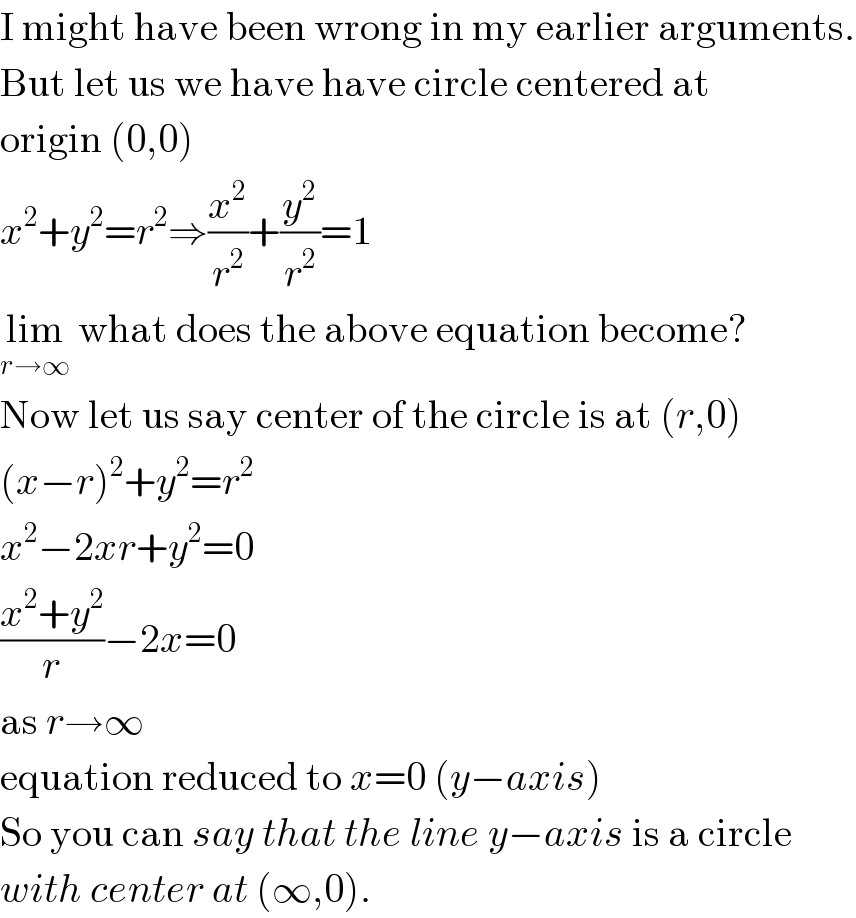
I might have been wrong in my earlier arguments. But let us we have have circle centered at origin (0,0) x^2 +y^2 =r^2 ⇒(x^2 /r^2 )+(y^2 /r^2 )=1 lim_(r→∞) what does the above equation become? Now let us say center of the circle is at (r,0) (x−r)^2 +y^2 =r^2 x^2 −2xr+y^2 =0 ((x^2 +y^2 )/r)−2x=0 as r→∞ equation reduced to x=0 (y−axis) So you can say that the line y−axis is a circle with center at (∞,0).

$$\mathrm{I}\:\mathrm{might}\:\mathrm{have}\:\mathrm{been}\:\mathrm{wrong}\:\mathrm{in}\:\mathrm{my}\:\mathrm{earlier}\:\mathrm{arguments}. \\ $$$$\mathrm{But}\:\mathrm{let}\:\mathrm{us}\:\mathrm{we}\:\mathrm{have}\:\mathrm{have}\:\mathrm{circle}\:\mathrm{centered}\:\mathrm{at} \\ $$$$\mathrm{origin}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \Rightarrow\frac{{x}^{\mathrm{2}} }{{r}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{r}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\underset{{r}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{what}\:\mathrm{does}\:\mathrm{the}\:\mathrm{above}\:\mathrm{equation}\:\mathrm{become}? \\ $$$$\mathrm{Now}\:\mathrm{let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{at}\:\left({r},\mathrm{0}\right) \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xr}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{r}}−\mathrm{2}{x}=\mathrm{0} \\ $$$$\mathrm{as}\:{r}\rightarrow\infty \\ $$$$\mathrm{equation}\:\mathrm{reduced}\:\mathrm{to}\:{x}=\mathrm{0}\:\left({y}−{axis}\right) \\ $$$$\mathrm{So}\:\mathrm{you}\:\mathrm{can}\:{say}\:{that}\:{the}\:{line}\:{y}−{axis}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle} \\ $$$${with}\:{center}\:{at}\:\left(\infty,\mathrm{0}\right).\: \\ $$

Commented by Rasheed Soomro last updated on 19/Dec/15

That is a point to think!

$$\mathcal{T}{hat}\:{is}\:{a}\:{point}\:{to}\:{think}! \\ $$

Commented by prakash jain last updated on 19/Dec/15

Also with x=0 being the circle also makes your earlier argument about half plane being the area valid. And all tangents are parallel. You were correct!

$$\mathrm{Also}\:\mathrm{with}\:{x}=\mathrm{0}\:\mathrm{being}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{also}\:\mathrm{makes} \\ $$$$\mathrm{your}\:\mathrm{earlier}\:\mathrm{argument}\:\mathrm{about}\:\mathrm{half}\:\mathrm{plane} \\ $$$$\mathrm{being}\:\mathrm{the}\:\mathrm{area}\:\mathrm{valid}. \\ $$$$\mathrm{And}\:\mathrm{all}\:\mathrm{tangents}\:\mathrm{are}\:\mathrm{parallel}. \\ $$$$\mathrm{You}\:\mathrm{were}\:\mathrm{correct}! \\ $$

Commented by Rasheed Soomro last updated on 20/Dec/15

An other term in which we can clear our idea is ′curveness′ As radius of circle gets greater the curveness gets smaller. For r=1, for curve of unit length the curveness is obvious.But for r=1000,it is not so obvious. So we can say: r→∞ ⇒ curveness→0 or curveness→straightness or circle→line

$${An}\:{other}\:{term}\:{in}\:{which}\:{we}\:{can}\:{clear} \\ $$$${our}\:{idea}\:{is}\:'{curveness}' \\ $$$${As}\:{radius}\:{of}\:{circle}\:{gets}\:{greater} \\ $$$${the}\:{curveness}\:{gets}\:{smaller}. \\ $$$${For}\:{r}=\mathrm{1},\:{for}\:{curve}\:{of}\:{unit}\:{length} \\ $$$${the}\:{curveness}\:{is}\:{obvious}.{But}\:{for} \\ $$$${r}=\mathrm{1000},{it}\:{is}\:{not}\:{so}\:{obvious}. \\ $$$${So}\:{we}\:{can}\:{say}: \\ $$$${r}\rightarrow\infty\:\Rightarrow\:{curveness}\rightarrow\mathrm{0} \\ $$$${or}\:{curveness}\rightarrow{straightness} \\ $$$${or} \\ $$$${circle}\rightarrow{line} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com