Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36957 by rahul 19 last updated on 07/Jun/18

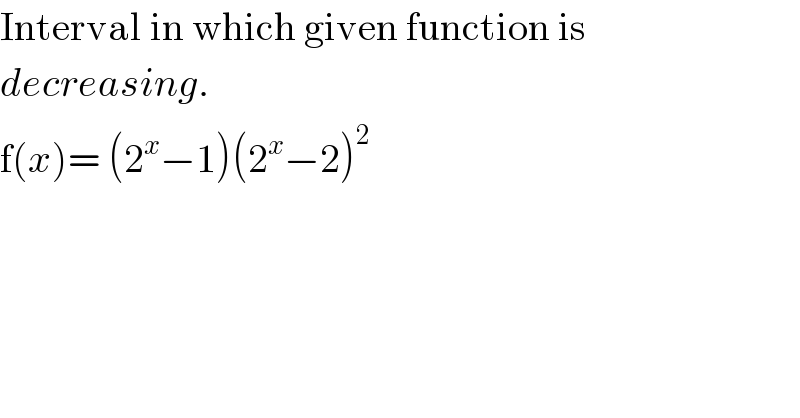
Interval in which given function is decreasing. f(x)= (2^x −1)(2^x −2)^2

$$\mathrm{Interval}\:\mathrm{in}\:\mathrm{which}\:\mathrm{given}\:\mathrm{function}\:\mathrm{is} \\ $$$${decreasing}. \\ $$$$\mathrm{f}\left({x}\right)=\:\left(\mathrm{2}^{{x}} −\mathrm{1}\right)\left(\mathrm{2}^{{x}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jun/18

y=(2^x −1)(2^x −2)^2 (dy/dx)=(2^x −1)×2(2^x −2)2^x ln2+(2^x −2)^2 ×2^x ×ln2 for decreasing (dy/dx)<0 (t−1)×2(t−2)tln2+ln2×)(t−2)^2 ×t ln2{2t×(t^2 −3t+2)+t(t^2 −4t+4)} =ln2{2t^3 −6t^2 +4t+t^3 −4t^2 +4t} =ln2{3t^3 −10t^2 +8t) =ln2{t(3t^2 −10t+8)} =ln2{t(3t^2 −6t−4t+8)} =ln2[t(3t(t−2)−4(t−2)∣ =ln2t(t−2)(3t−4) critical value of t=0,t=2 ,(4/3) 2^x =0 x→−∞ 2^x =2 x=1 2^x =(4/3) x=0.41(approx) when t>2 i,e x>1 (dy/dx)>0 increasing when 2>t>(4/3) 1>x>0.41 (dy/dx)<0 decreasing when (4/3)>t>0 0.41>x>−∞ (dy/dx)>0 increasing when 0>t x→−∞ (dy/dx)<0 decreasing

$${y}=\left(\mathrm{2}^{{x}} −\mathrm{1}\right)\left(\mathrm{2}^{{x}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\left(\mathrm{2}^{{x}} −\mathrm{1}\right)×\mathrm{2}\left(\mathrm{2}^{{x}} −\mathrm{2}\right)\mathrm{2}^{{x}} {ln}\mathrm{2}+\left(\mathrm{2}^{{x}} −\mathrm{2}\right)^{\mathrm{2}} ×\mathrm{2}^{{x}} ×{ln}\mathrm{2} \\ $$$${for}\:{decreasing}\:\frac{{dy}}{{dx}}<\mathrm{0} \\ $$$$\left.\left({t}−\mathrm{1}\right)×\mathrm{2}\left({t}−\mathrm{2}\right){tln}\mathrm{2}+{ln}\mathrm{2}×\right)\left({t}−\mathrm{2}\right)^{\mathrm{2}} ×{t} \\ $$$${ln}\mathrm{2}\left\{\mathrm{2}{t}×\left({t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{2}\right)+{t}\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}\right)\right\} \\ $$$$={ln}\mathrm{2}\left\{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{6}{t}^{\mathrm{2}} +\mathrm{4}{t}+{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}\right\} \\ $$$$={ln}\mathrm{2}\left\{\mathrm{3}{t}^{\mathrm{3}} −\mathrm{10}{t}^{\mathrm{2}} +\mathrm{8}{t}\right) \\ $$$$={ln}\mathrm{2}\left\{{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{10}{t}+\mathrm{8}\right)\right\} \\ $$$$={ln}\mathrm{2}\left\{{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{4}{t}+\mathrm{8}\right)\right\} \\ $$$$={ln}\mathrm{2}\left[{t}\left(\mathrm{3}{t}\left({t}−\mathrm{2}\right)−\mathrm{4}\left({t}−\mathrm{2}\right)\mid\right.\right. \\ $$$$={ln}\mathrm{2}{t}\left({t}−\mathrm{2}\right)\left(\mathrm{3}{t}−\mathrm{4}\right) \\ $$$${critical}\:{value}\:\:{of}\:{t}=\mathrm{0},{t}=\mathrm{2}\:,\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{2}^{{x}} =\mathrm{0}\:\:\:{x}\rightarrow−\infty \\ $$$$\mathrm{2}^{{x}} =\mathrm{2}\:\:{x}=\mathrm{1} \\ $$$$\mathrm{2}^{{x}} =\frac{\mathrm{4}}{\mathrm{3}}\:\:{x}=\mathrm{0}.\mathrm{41}\left({approx}\right) \\ $$$${when}\:{t}>\mathrm{2}\:{i},{e}\:{x}>\mathrm{1}\:\:\frac{{dy}}{{dx}}>\mathrm{0}\:\:{increasing} \\ $$$${when}\:\:\mathrm{2}>{t}>\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\:\mathrm{1}>{x}>\mathrm{0}.\mathrm{41}\:\:\frac{{dy}}{{dx}}<\mathrm{0}\:\:{decreasing} \\ $$$${when}\:\frac{\mathrm{4}}{\mathrm{3}}>{t}>\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}.\mathrm{41}>{x}>−\infty\:\:\frac{{dy}}{{dx}}>\mathrm{0}\:{increasing} \\ $$$${when}\:\mathrm{0}>{t}\:\:\:{x}\rightarrow−\infty\:\:\:\frac{{dy}}{{dx}}<\mathrm{0}\:\:{decreasing} \\ $$$$ \\ $$$$ \\ $$

Answered by ajfour last updated on 07/Jun/18

let u=2^x ⇒ (du/dx)=2^x ln 2 y=(u−1)(u−2)^2 (dy/dx)=[(u−2)^2 +2(u−1)(u−2)](2^z ln 2) =(2^x ln 2)(u−2)(3u−4) (dy/dx) ≤ 0 ⇒ (4/3) ≤ 2^x ≤ 2 ((2ln 2−ln 3)/(ln 2)) ≤ x ≤ 1 .

$${let}\:\:\:{u}=\mathrm{2}^{{x}} \:\:\Rightarrow\:\:\frac{{du}}{{dx}}=\mathrm{2}^{{x}} \mathrm{ln}\:\mathrm{2} \\ $$$${y}=\left({u}−\mathrm{1}\right)\left({u}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\left[\left({u}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left({u}−\mathrm{1}\right)\left({u}−\mathrm{2}\right)\right]\left(\mathrm{2}^{{z}} \mathrm{ln}\:\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\left(\mathrm{2}^{{x}} \mathrm{ln}\:\mathrm{2}\right)\left({u}−\mathrm{2}\right)\left(\mathrm{3}{u}−\mathrm{4}\right) \\ $$$$\frac{{dy}}{{dx}}\:\leqslant\:\mathrm{0}\:\Rightarrow\:\frac{\mathrm{4}}{\mathrm{3}}\:\leqslant\:\mathrm{2}^{{x}} \:\leqslant\:\mathrm{2} \\ $$$$\:\:\frac{\mathrm{2ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}\:\:\leqslant\:\:{x}\:\:\leqslant\:\:\mathrm{1}\:\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com