Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36965 by MJS last updated on 07/Jun/18

$$\int \frac{x^5-x^4+x^3-1}{{(x^2-x+1)}^3}dx=$$

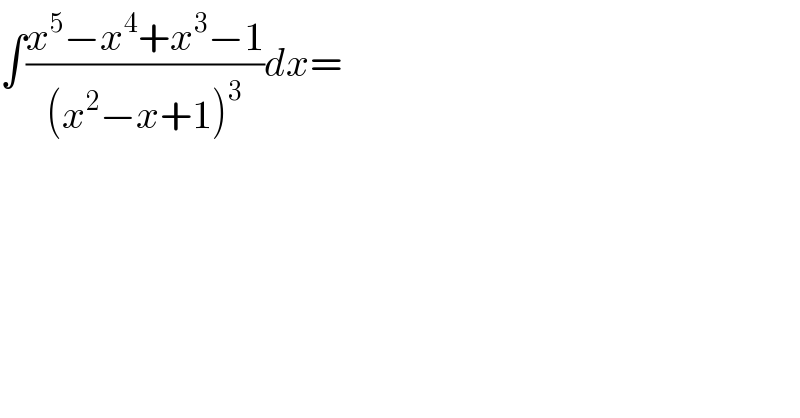
Commented by rahul 19 last updated on 07/Jun/18

$$\mathrm{is}\mathrm{ostradosgki}\mathrm{method}\mathrm{applicable}\mathrm{here}?$$

Commented by MJS last updated on 07/Jun/18

$${\mathrm{I}}^{\prime }\mathrm{ll}\mathrm{post}\mathrm{a}\mathrm{faster}\mathrm{method}\mathrm{tomorrow}$$

Commented by MJS last updated on 07/Jun/18

$$\mathrm{yes}\mathrm{Sir}!$$

Answered by MJS last updated on 07/Jun/18

$$\mathrm{Standard}\mathrm{Method}$$$$\int \frac{x^5-x^4+x^3-1}{{(x^2-x+1)}^3}dx=$$$$=\int \frac{x+1}{x^2-x+1}dx-\int \frac{dx}{{(x^2-x+1)}^2}-\int \frac{dx}{{(x^2-x+1)}^3}=$$$$$$$$\int \frac{x+1}{x^2-x+1}dx=\frac{1}{2}\int \frac{2x-1}{x^2-x+1}dx+\frac{3}{2}\int \frac{dx}{x^2-x+1}=$$$$$$$$\frac{1}{2}\int \frac{2x-1}{x^2-x+1}dx=$$$$[t=x^2-x+1\to dx=\frac{dt}{2x-1}]$$$$=\frac{1}{2}\int \frac{dt}{t}=\frac{1}{2}\ln t=\frac{1}{2}\ln (x^2-x+1)$$$$$$$$\frac{3}{2}\int \frac{dx}{x^2-x+1}=\frac{3}{2}\int \frac{dx}{{(x-\frac{1}{2})}^2+\frac{3}{4}}=$$$$[t=\frac{\sqrt{3}}{3}(2x-1)\to dx=\frac{\sqrt{3}}{2}dt]$$$$=\sqrt{3}\int \frac{dt}{t^2+1}=\frac{2\sqrt{3}}{3}\arctan t=$$$$=\sqrt{3}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$=\frac{1}{2}\ln (x^2-x+1)+\sqrt{3}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$\int \frac{dx}{{(x^2-x+1)}^2}=16\int \frac{dx}{{({(2x-1)}^2+3)}^2}=$$$$[t=2x-1\to dx=\frac{dt}{2}]$$$$=8\int \frac{dt}{{(t^2+3)}^2}=$$$$[\int \frac{dt}{{({at}^2+b)}^n}=\frac{t}{2b(n-1){({at}^2+b)}^{n-1}}+$$$$+\frac{2n-3}{2b(n-1)}\int \frac{dt}{{({at}^2+b)}^{n-1}}]$$$$=8(\frac{t}{6(t^2+3)}+\frac{1}{6}\int \frac{dt}{t^2+3})=$$$$$$$$\frac{1}{6}\int \frac{dt}{t^2+3}=$$$$[u=\frac{\sqrt{3}}{3}t\to dt=\sqrt{3}du]$$$$=\frac{\sqrt{3}}{18}\int \frac{du}{u^2+1}=\frac{\sqrt{3}}{3}\arctan u=$$$$=\frac{\sqrt{3}}{18}\arctan \left(\frac{\sqrt{3}}{3}t\right)$$$$$$$$=8(\frac{t}{6(t^2+3)}+\frac{\sqrt{3}}{18}\arctan \left(\frac{\sqrt{3}}{3}t\right))=$$$$=\frac{2x-1}{3(x^2-x+1)}+\frac{4\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$\int \frac{dx}{{(x^2-x+1)}^3}=64\int \frac{dx}{{({(2x-1)}^2+3)}^3}=$$$$[t=2x-1\to dx=\frac{dt}{2}]$$$$=32\int \frac{dt}{{(t^2+3)}^3}=$$$$[\int \frac{dt}{{({at}^2+b)}^n}=\frac{t}{2b(n-1){({at}^2+b)}^{n-1}}+$$$$+\frac{2n-3}{2b(n-1)}\int \frac{dt}{{({at}^2+b)}^{n-1}}]$$$$=32(\frac{t}{12{(t^2+3)}^2}+\frac{1}{4}\int \frac{dt}{{(t^2+3)}^2})=$$$$=32(\frac{t}{12{(t^2+3)}^2}+\frac{1}{4}(\frac{t}{6(t^2+3)}+\frac{1}{6}\int \frac{dt}{t^2+3}))=$$$$=\frac{8t}{3{(t^2+3)}^2}+\frac{4t}{3(t^2+3)}+\frac{4\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}t\right)=$$$$=\frac{4t(t^2+5)}{3{(t^2+3)}^2}+\frac{4\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}t\right)=$$$$=\frac{(2x-1)(2x^2-2x+3)}{6{(x^2-x+1)}^2}+\frac{4\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$=\frac{1}{2}\ln (x^2-x+1)+\frac{\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)-$$$$-\frac{(2x-1)(4x^2-4x+5)}{6{(x^2-x+1)}^2}+C$$

Answered by MJS last updated on 07/Jun/18

$${\mathrm{Ostrogradski}}^{\prime }\mathrm{s}\mathrm{Method}$$$$\int \frac{P}{Q}=\frac{P_1}{Q_1}+\int \frac{P_2}{Q_2}$$$$P=x^5-x^4+x^3-1$$$$Q={(x^2-x+1)}^3$$$$Q^{\prime }=3(2x-1){(x^2-x+1)}^2$$$$Q_1=\gcd (Q,Q^{\prime })={(x^2-x+1)}^2$$$$Q_2=\frac{Q}{Q_1}=x^2-x+1$$$$\mathrm{grade}\left(P_i\right)<\mathrm{grade}\left(Q_i\right)\Rightarrow$$$$P_1=c_1{x}^3+c_2{x}^2+c_{3}x+c_4$$$$P_2=c_{5}x+c_6$$$$\mathrm{differentiate}\mathrm{both}\mathrm{sides}\mathrm{of}\int \frac{P}{Q}=\frac{P_1}{Q_1}+\int \frac{P_2}{Q_2}$$$$\frac{P}{Q}=\frac{P_1^{\prime }{Q}_1-P_1{Q}_1^{\prime }}{Q_1^2}+\frac{P_2}{Q_2}\Rightarrow$$$$\left(\mathrm{this}\mathrm{is}\mathrm{the}\mathrm{hardest}\mathrm{part}\right)$$$$\Rightarrow$$$$c_5=1$$$$-(c_1+2c_5-c_6)=-1$$$$-(c_1+2c_2-3c_5+2c_6)=1$$$$3c_1-3c_3-2c_5+3c_6=0$$$$2c_2+c_3-4c_4+c_5-2c_6=0$$$$c_3+2c_4+c_6=-1$$$$$$$$c_1=-\frac{4}{3};c_2=3;c_3=-\frac{7}{3};c_4=\frac{5}{6};c_5=1;c_6=-\frac{1}{3}$$$$$$$$P_1=-\frac{4}{3}{x}^3+2x^2-\frac{7}{3}x+\frac{5}{6}$$$$P_2=x-\frac{1}{3}$$$$$$$$\int \frac{x^5-x^4+x^3-1}{{(x^2-x+1)}^3}dx$$$$=\frac{-\frac{4}{3}{x}^3+2x^2-\frac{7}{3}x+\frac{5}{6}}{{(x^2-x+1)}^2}+\int \frac{x-\frac{1}{3}}{x^2-x+1}dx=$$$$=-\frac{8x^3-12x^2+14x-5}{6{(x^2-x+1)}^2}+\int \frac{3x-1}{3(x^2-x+1)}dx=$$$$$$$$\int \frac{3x-1}{3(x^2-x+1)}dx=\frac{1}{3}\int \frac{3x-1}{x^2-x+1}dx=$$$$\frac{1}{3}(\frac{3}{2}\int \frac{2x-1}{x^2-x+1}dx+\frac{1}{2}\int \frac{dx}{x^2-x+1})=$$$$\frac{1}{2}\int \frac{2x-1}{x^2-x+1}dx+\frac{1}{6}\int \frac{dx}{x^2-x+1}=$$$$$$$$\frac{1}{2}\int \frac{2x-1}{x^2-x+1}dx=$$$$[t=x^2-x+1\to dx=\frac{dt}{2x-1}]$$$$=\frac{1}{2}\int \frac{dt}{t}=\frac{1}{2}\ln t=\frac{1}{2}\ln (x^2-x+1)$$$$$$$$\frac{1}{6}\int \frac{dx}{x^2-x+1}=\frac{1}{6}\int \frac{dx}{{(x-\frac{1}{2})}^2+\frac{3}{4}}=$$$$[t=\frac{\sqrt{3}}{3}(2x-1)\to dx=\frac{\sqrt{3}}{2}dt]$$$$\frac{\sqrt{3}}{9}\int \frac{dt}{t^2+1}=\frac{\sqrt{3}}{9}\arctan t=$$$$=\frac{\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$=\frac{1}{2}\ln (x^2-x+1)+\frac{\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)$$$$$$$$=\frac{1}{2}\ln (x^2-x+1)+\frac{\sqrt{3}}{9}\arctan \left(\frac{\sqrt{3}}{3}(2x-1)\right)-$$$$-\frac{8x^3-12x^2+14x-5}{6{(x^2-x+1)}^2}+C$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com