Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36997 by rahul 19 last updated on 07/Jun/18

∫ (√(((1+x)/x) ))dx = ?

$$\int\:\sqrt{\frac{\mathrm{1}+{x}}{{x}}\:}{dx}\:=\:? \\ $$

Commented by behi83417@gmail.com last updated on 07/Jun/18

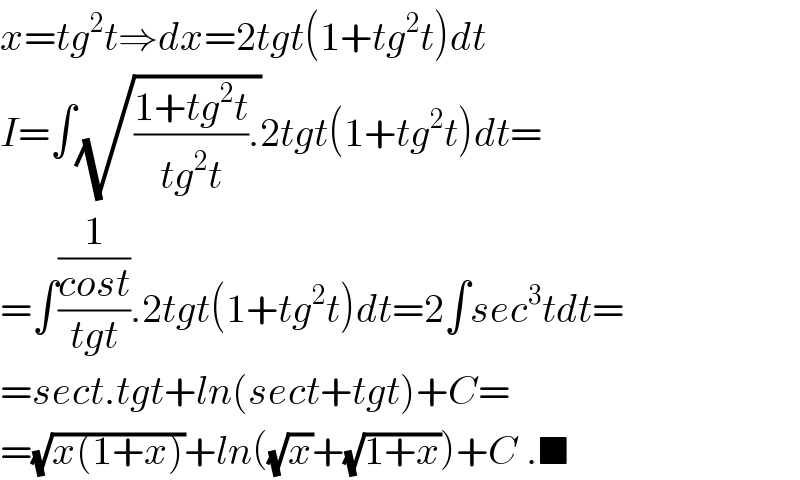
x=tg^2 t⇒dx=2tgt(1+tg^2 t)dt I=∫(√(((1+tg^2 t)/(tg^2 t)).))2tgt(1+tg^2 t)dt= =∫((1/(cost))/(tgt)).2tgt(1+tg^2 t)dt=2∫sec^3 tdt= =sect.tgt+ln(sect+tgt)+C= =(√(x(1+x)))+ln((√x)+(√(1+x)))+C .■

$${x}={tg}^{\mathrm{2}} {t}\Rightarrow{dx}=\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt} \\ $$$${I}=\int\sqrt{\frac{\mathrm{1}+{tg}^{\mathrm{2}} {t}}{{tg}^{\mathrm{2}} {t}}.}\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}= \\ $$$$=\int\frac{\frac{\mathrm{1}}{{cost}}}{{tgt}}.\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}=\mathrm{2}\int{sec}^{\mathrm{3}} {tdt}= \\ $$$$={sect}.{tgt}+{ln}\left({sect}+{tgt}\right)+{C}= \\ $$$$=\sqrt{{x}\left(\mathrm{1}+{x}\right)}+{ln}\left(\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}\right)+{C}\:.\blacksquare \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jun/18

∫((1+x)/(√(x+x^2 )))dx (1/2)∫((1+1+2x)/(√(x+x^2 )))dx =(1/2)∫(dx/(√(x^2 +2.x.(1/2)+(1/4)−(1/4))))+(1/2)∫((d(x+x^2 ))/(√(x+x^2 ))) =(1/2)∫(dx/(√((x+(1/2))^2 −((1/2))^2 ))) +(1/2)×(((x+x^2 )^(1/2) )/(1/2)) use formula ∫(dx/(√(X^2 −A^2 )))

$$\int\frac{\mathrm{1}+{x}}{\sqrt{{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{1}+\mathrm{2}{x}}{\sqrt{{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+{x}^{\mathrm{2}} \right)}{\sqrt{{x}+{x}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({x}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${use}\:{formula}\:\int\frac{{dx}}{\sqrt{{X}^{\mathrm{2}} −{A}^{\mathrm{2}} }} \\ $$

Answered by MJS last updated on 07/Jun/18

∫(√((1+x)/x))dx=∫((√(1+x))/(√x))dx= [t=(√x) → dx=2(√x)dt] =2∫(√(1+t^2 ))= [u=arctan t → dt=sec^2 u du] =2∫sec^2 u (√(1+tan^2 u)) du=2∫sec^3 u du= [∫sec^n u du=((sec^(n−2) u tan u)/(n−1))+((n−2)/(n−1))∫sec^(n−2) u du] =sec u tan u +∫sec u du= =sec u tan u +ln(sec u +tan u)= =t(√(1+t^2 ))+ln((√(1+t^2 ))+t)= =(√(x(1+x)))+ln((√(1+x))+(√x))+C

$$\int\sqrt{\frac{\mathrm{1}+{x}}{{x}}}{dx}=\int\frac{\sqrt{\mathrm{1}+{x}}}{\sqrt{{x}}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{arctan}\:{t}\:\rightarrow\:{dt}=\mathrm{sec}^{\mathrm{2}} \:{u}\:{du}\right] \\ $$$$=\mathrm{2}\int\mathrm{sec}^{\mathrm{2}} \:{u}\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{u}}\:{du}=\mathrm{2}\int\mathrm{sec}^{\mathrm{3}} \:{u}\:{du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\int\mathrm{sec}^{{n}} \:{u}\:{du}=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:\mathrm{tan}\:{u}}{{n}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:{du}\right] \\ $$$$=\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}\:+\int\mathrm{sec}\:{u}\:{du}= \\ $$$$=\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}\:+\mathrm{ln}\left(\mathrm{sec}\:{u}\:+\mathrm{tan}\:{u}\right)= \\ $$$$={t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{ln}\left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+{t}\right)= \\ $$$$=\sqrt{{x}\left(\mathrm{1}+{x}\right)}+\mathrm{ln}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com