Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 37137 by rahul 19 last updated on 09/Jun/18

Find minimum distance between y^2 =8x and x^2 +(y+6)^2 =1.

$$\mathrm{Find}\:\mathrm{minimum}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{y}^{\mathrm{2}} =\mathrm{8}{x}\:{and}\:{x}^{\mathrm{2}} +\left({y}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{1}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jun/18

from graph it is seen that(2,−4) lies on y^2 =8x (2,−4) is nearest point to the circle distance between centre of circle(0,−6) and (2,−4 is (√((2−0)^2 +(−4+6)^2 )) =(√(4+4)) =2(√2) so minimum distance=2(√2) −1 pls check

$${from}\:{graph}\:{it}\:{is}\:{seen}\:{that}\left(\mathrm{2},−\mathrm{4}\right)\:{lies}\:{on}\:{y}^{\mathrm{2}} =\mathrm{8}{x} \\ $$$$\left(\mathrm{2},−\mathrm{4}\right)\:{is}\:{nearest}\:{point}\:{to}\:{the}\:{circle} \\ $$$${distance}\:{between}\:{centre}\:{of}\:{circle}\left(\mathrm{0},−\mathrm{6}\right)\:{and}\: \\ $$$$\left(\mathrm{2},−\mathrm{4}\:{is}\right. \\ $$$$\sqrt{\left(\mathrm{2}−\mathrm{0}\right)^{\mathrm{2}} +\left(−\mathrm{4}+\mathrm{6}\right)^{\mathrm{2}} \:}\:\:=\sqrt{\mathrm{4}+\mathrm{4}}\:\:=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${so}\:{minimum}\:{distance}=\mathrm{2}\sqrt{\mathrm{2}}\:\:−\mathrm{1} \\ $$$${pls}\:{check} \\ $$

Commented by rahul 19 last updated on 09/Jun/18

Sir, how do you conclude (2,−4) is the nearest point to circle. Also sol. using parametric coordinates is welcome!

$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{conclude}\:\left(\mathrm{2},−\mathrm{4}\right)\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{nearest}\:\mathrm{point}\:\mathrm{to}\:\mathrm{circle}. \\ $$$$\mathrm{Also}\:\mathrm{sol}.\:\mathrm{using}\:\mathrm{parametric}\:\mathrm{coordinates} \\ $$$$\mathrm{is}\:\mathrm{welcome}! \\ $$

Commented by rahul 19 last updated on 09/Jun/18

I have made this random problem myself so i don′t have any answer.

$$\mathrm{I}\:\mathrm{have}\:\mathrm{made}\:\mathrm{this}\:\mathrm{random}\:\mathrm{problem}\:\mathrm{myself} \\ $$$$\mathrm{so}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{any}\:\mathrm{answer}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Jun/18

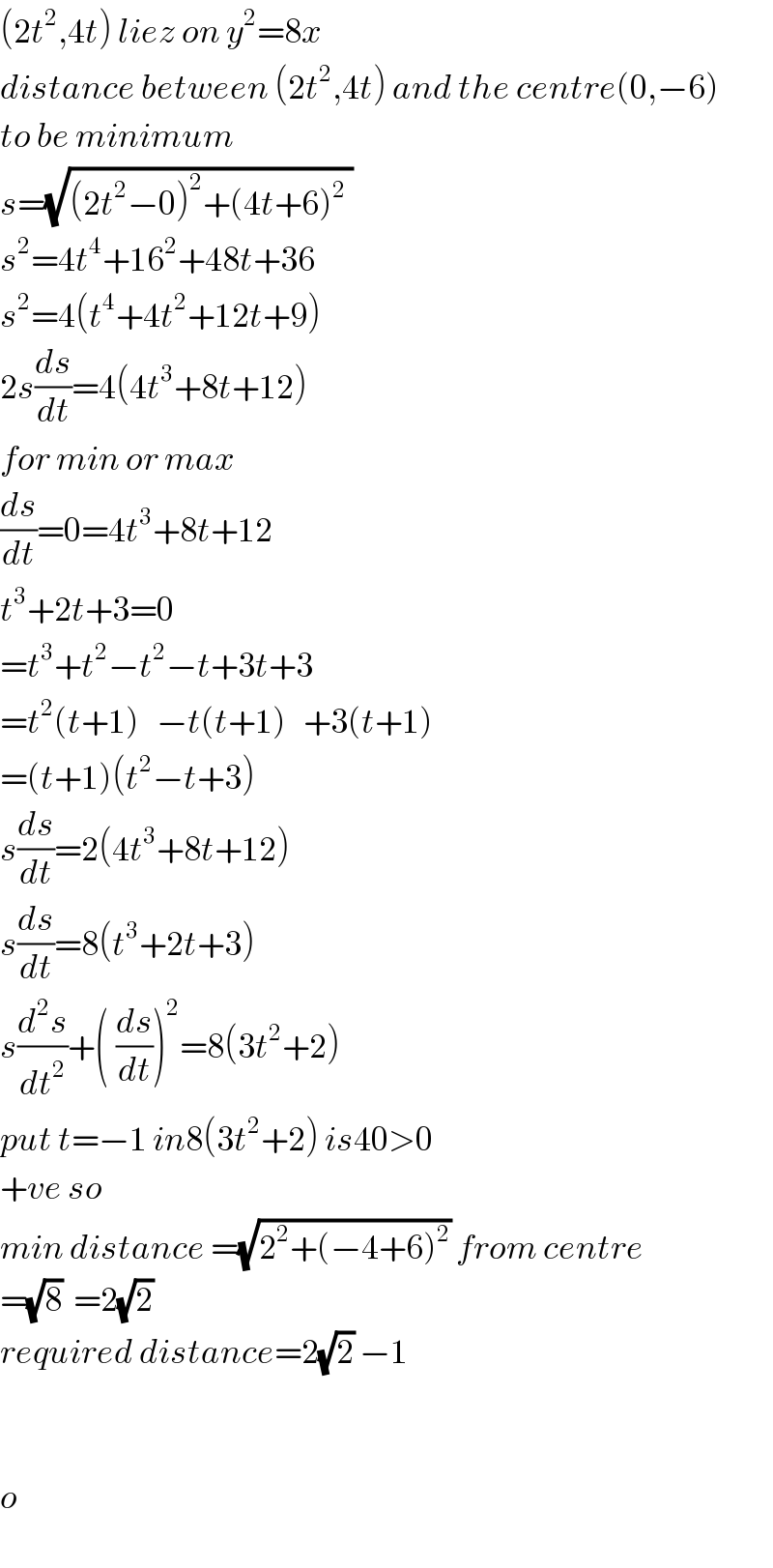
(2t^2 ,4t) liez on y^2 =8x distance between (2t^2 ,4t) and the centre(0,−6) to be minimum s=(√((2t^2 −0)^2 +(4t+6)^2 )) s^2 =4t^4 +16^2 +48t+36 s^2 =4(t^4 +4t^2 +12t+9) 2s(ds/dt)=4(4t^3 +8t+12) for min or max (ds/dt)=0=4t^3 +8t+12 t^3 +2t+3=0 =t^3 +t^2 −t^2 −t+3t+3 =t^2 (t+1) −t(t+1) +3(t+1) =(t+1)(t^2 −t+3) s(ds/dt)=2(4t^3 +8t+12) s(ds/dt)=8(t^3 +2t+3) s(d^2 s/dt^2 )+(^ (ds/dt))^2 =8(3t^2 +2) put t=−1 in8(3t^2 +2) is40>0 +ve so min distance =(√(2^2 +(−4+6)^2 )) from centre =(√8) =2(√2) required distance=2(√2) −1 o

$$\left(\mathrm{2}{t}^{\mathrm{2}} ,\mathrm{4}{t}\right)\:{liez}\:{on}\:{y}^{\mathrm{2}} =\mathrm{8}{x} \\ $$$${distance}\:{between}\:\left(\mathrm{2}{t}^{\mathrm{2}} ,\mathrm{4}{t}\right)\:{and}\:{the}\:{centre}\left(\mathrm{0},−\mathrm{6}\right) \\ $$$${to}\:{be}\:{minimum} \\ $$$${s}=\sqrt{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{4}{t}+\mathrm{6}\right)^{\mathrm{2}} \:} \\ $$$${s}^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{4}} +\mathrm{16}^{\mathrm{2}} +\mathrm{48}{t}+\mathrm{36} \\ $$$${s}^{\mathrm{2}} =\mathrm{4}\left({t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{12}{t}+\mathrm{9}\right) \\ $$$$\mathrm{2}{s}\frac{{ds}}{{dt}}=\mathrm{4}\left(\mathrm{4}{t}^{\mathrm{3}} +\mathrm{8}{t}+\mathrm{12}\right) \\ $$$${for}\:{min}\:{or}\:{max} \\ $$$$\frac{{ds}}{{dt}}=\mathrm{0}=\mathrm{4}{t}^{\mathrm{3}} +\mathrm{8}{t}+\mathrm{12} \\ $$$${t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{3}=\mathrm{0} \\ $$$$={t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{t}^{\mathrm{2}} −{t}+\mathrm{3}{t}+\mathrm{3} \\ $$$$={t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)\:\:\:−{t}\left({t}+\mathrm{1}\right)\:\:\:+\mathrm{3}\left({t}+\mathrm{1}\right) \\ $$$$=\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{3}\right) \\ $$$${s}\frac{{ds}}{{dt}}=\mathrm{2}\left(\mathrm{4}{t}^{\mathrm{3}} +\mathrm{8}{t}+\mathrm{12}\right) \\ $$$${s}\frac{{ds}}{{dt}}=\mathrm{8}\left({t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{3}\right) \\ $$$${s}\frac{{d}^{\mathrm{2}} {s}}{{dt}^{\mathrm{2}} }+\left(^{} \frac{{ds}}{{dt}}\right)^{\mathrm{2}} =\mathrm{8}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$${put}\:{t}=−\mathrm{1}\:{in}\mathrm{8}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}\right)\:{is}\mathrm{40}>\mathrm{0} \\ $$$$+{ve}\:{so} \\ $$$${min}\:{distance}\:=\sqrt{\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{4}+\mathrm{6}\right)^{\mathrm{2}} }\:{from}\:{centre} \\ $$$$=\sqrt{\mathrm{8}}\:\:=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${required}\:{distance}=\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$${o} \\ $$

Answered by MJS last updated on 10/Sep/18

the minimum distance between the circle and the parabola is the mininum distance between the center of the circle and the parabola minus the radius of the circle P∈par (negative branch): P= ((x),((−2(√(2x)))) ) center of circle: C= ((0),((−6)) ) ∣PC∣^2 =x^2 +(−6+2(√(2x)))^2 =x^2 +8x−24(√(2x))+36 (d/dx)[x^2 +8x−24(√(2x))+36]=0 2x−((12(√(2x)))/x)+8=0 ⇒ ⇒ x(x−2)(x^2 +10x+36)=0 x_1 =0 is a local maximum x_2 =2 is a local minimum P= ((2),((−4)) ) ∣PC∣=(√(x^2 +8x−24(√(2x))+36))=2(√2) minimum distance =∣PC∣−r=2(√2)−1

$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{parabola}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mininum}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{the}\:\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{and}\:\mathrm{the}\:\mathrm{parabola} \\ $$$$\mathrm{minus}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$ \\ $$$${P}\in{par}\:\left(\mathrm{negative}\:\mathrm{branch}\right):\:{P}=\begin{pmatrix}{{x}}\\{−\mathrm{2}\sqrt{\mathrm{2}{x}}}\end{pmatrix} \\ $$$$\mathrm{center}\:\mathrm{of}\:\mathrm{circle}:\:{C}=\begin{pmatrix}{\mathrm{0}}\\{−\mathrm{6}}\end{pmatrix} \\ $$$$\mid{PC}\mid^{\mathrm{2}} ={x}^{\mathrm{2}} +\left(−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{2}{x}}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{24}\sqrt{\mathrm{2}{x}}+\mathrm{36} \\ $$$$\frac{{d}}{{dx}}\left[{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{24}\sqrt{\mathrm{2}{x}}+\mathrm{36}\right]=\mathrm{0} \\ $$$$\mathrm{2}{x}−\frac{\mathrm{12}\sqrt{\mathrm{2}{x}}}{{x}}+\mathrm{8}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{36}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{local}\:\mathrm{maximum} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}\:\mathrm{is}\:\mathrm{a}\:\mathrm{local}\:\mathrm{minimum} \\ $$$$ \\ $$$${P}=\begin{pmatrix}{\mathrm{2}}\\{−\mathrm{4}}\end{pmatrix} \\ $$$$\mid{PC}\mid=\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{24}\sqrt{\mathrm{2}{x}}+\mathrm{36}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{minimum}\:\mathrm{distance}\:=\mid{PC}\mid−{r}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1} \\ $$

Commented by ajfour last updated on 09/Jun/18

Great! Sir. (but why did you delete your post of several integration questions?)

$${Great}!\:{Sir}. \\ $$$$\left({but}\:{why}\:{did}\:{you}\:{delete}\:{your}\:{post}\right. \\ $$$$\left.{of}\:{several}\:{integration}\:{questions}?\right) \\ $$

Commented by MJS last updated on 09/Jun/18

I made some mistakes, will post the corrected version soon

$$\mathrm{I}\:\mathrm{made}\:\mathrm{some}\:\mathrm{mistakes},\:\mathrm{will}\:\mathrm{post}\:\mathrm{the}\:\mathrm{corrected} \\ $$$$\mathrm{version}\:\mathrm{soon} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com