Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3716 by Yozzii last updated on 19/Dec/15

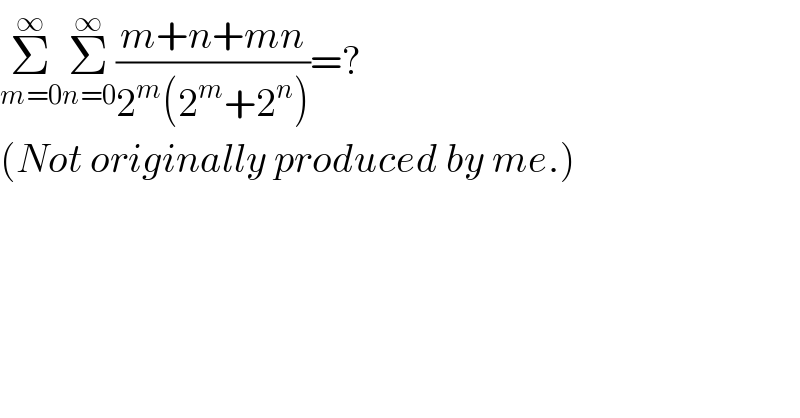
Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+mn)/(2^m (2^m +2^n )))=? (Not originally produced by me.)

$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{m}+{n}+{mn}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}=?\: \\ $$$$\left({Not}\:{originally}\:{produced}\:{by}\:{me}.\right) \\ $$

Commented by prakash jain last updated on 19/Dec/15

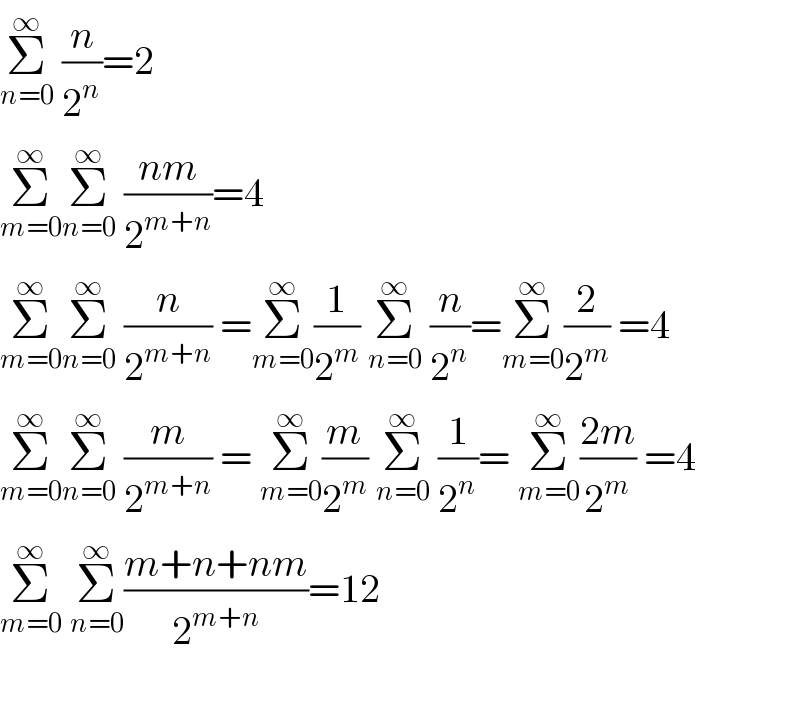
Σ_(n=0) ^∞ (n/2^n )=2 Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((nm)/2^(m+n) )=4 Σ_(m=0) ^∞ Σ_(n=0) ^∞ (n/2^(m+n) ) =Σ_(m=0) ^∞ (1/2^m ) Σ_(n=0) ^∞ (n/2^n )=Σ_(m=0) ^∞ (2/2^m ) =4 Σ_(m=0) ^∞ Σ_(n=0) ^∞ (m/2^(m+n) ) = Σ_(m=0) ^∞ (m/2^m ) Σ_(n=0) ^∞ (1/2^n )= Σ_(m=0) ^∞ ((2m)/2^m ) =4 Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/2^(m+n) )=12

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{n}}{\mathrm{2}^{{n}} }=\mathrm{2} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{nm}}{\mathrm{2}^{{m}+{n}} }=\mathrm{4} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{n}}{\mathrm{2}^{{m}+{n}} }\:=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{m}} }\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{n}}{\mathrm{2}^{{n}} }=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{2}^{{m}} }\:=\mathrm{4} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}}{\mathrm{2}^{{m}+{n}} }\:=\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{m}}{\mathrm{2}^{{m}} }\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{m}}{\mathrm{2}^{{m}} }\:=\mathrm{4} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}+{n}} }=\mathrm{12} \\ $$$$ \\ $$

Commented by prakash jain last updated on 19/Dec/15

case 1: m=n=0 ((m+n+mn)/(2^m (2^m +2^n )))=0 ((m+n+nm)/2^(m+n) )=0 case 2:m and are both not 0 ((m+n+mn)/(2^m (2^m +2^n )))−((m+n+nm)/2^(m+n) ) (m+n+mn)[(1/(2^m (2^m +2^n )))−(1/2^(m+n) )] ((m+n+nm)/(2^m 2^(m+n) (2^m +2^n )))(2^(m+n) −2^(2m) −2^(m+n) ) =−((2^(2m) (m+n+mn))/(2^m 2^(m+n) (2^m +2^n )))<0 for all m,n so Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+mn)/(2^m (2^m +2^n ))) converges.

$${case}\:\mathrm{1}:\:{m}={n}=\mathrm{0} \\ $$$$\frac{{m}+{n}+{mn}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}=\mathrm{0}\:\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}+{n}} }=\mathrm{0} \\ $$$$\mathrm{case}\:\mathrm{2}:{m}\:{and}\:{are}\:{both}\:{not}\:\mathrm{0} \\ $$$$\frac{{m}+{n}+{mn}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}−\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}+{n}} } \\ $$$$\left({m}+{n}+{mn}\right)\left[\frac{\mathrm{1}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}−\frac{\mathrm{1}}{\mathrm{2}^{{m}+{n}} }\right] \\ $$$$\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}} \mathrm{2}^{{m}+{n}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}\left(\mathrm{2}^{{m}+{n}} −\mathrm{2}^{\mathrm{2}{m}} −\mathrm{2}^{{m}+{n}} \right) \\ $$$$=−\frac{\mathrm{2}^{\mathrm{2}{m}} \left({m}+{n}+{mn}\right)}{\mathrm{2}^{{m}} \mathrm{2}^{{m}+{n}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}<\mathrm{0}\:{for}\:{all}\:{m},{n} \\ $$$${so} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{mn}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}\:\mathrm{converges}. \\ $$

Commented by Yozzii last updated on 19/Dec/15

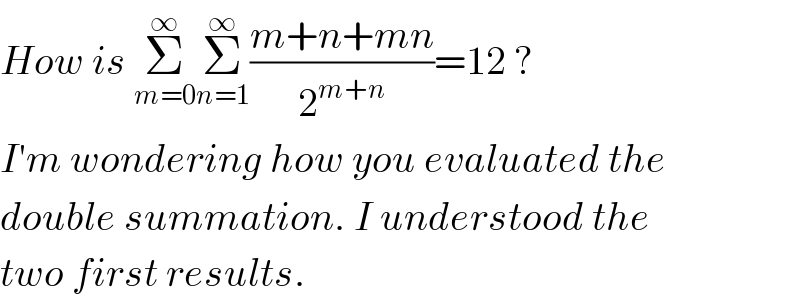
How is Σ_(m=0) ^∞ Σ_(n=1) ^∞ ((m+n+mn)/2^(m+n) )=12 ? I′m wondering how you evaluated the double summation. I understood the two first results.

$${How}\:{is}\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{m}+{n}+{mn}}{\mathrm{2}^{{m}+{n}} }=\mathrm{12}\:? \\ $$$${I}'{m}\:{wondering}\:{how}\:{you}\:{evaluated}\:{the} \\ $$$${double}\:{summation}.\:{I}\:{understood}\:{the} \\ $$$${two}\:{first}\:{results}.\: \\ $$

Commented by prakash jain last updated on 19/Dec/15

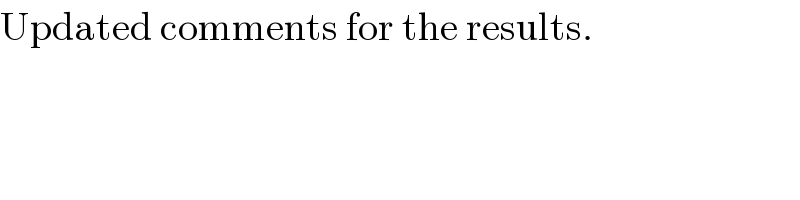
Updated comments for the results.

$$\mathrm{Updated}\:\mathrm{comments}\:\mathrm{for}\:\mathrm{the}\:\mathrm{results}. \\ $$

Commented by Yozzii last updated on 19/Dec/15

Thanks.

$${Thanks}. \\ $$

Answered by prakash jain last updated on 19/Dec/15

Not sure of the answer. Please verify ((m+n+nm)/(2^m (2^m +2^n )))=((m+n+nm)/2^n )[(1/2^m )−(1/(2^n +2^m ))] Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/(2^m (2^m +2^n ))) =Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/2^(n+m) )−Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/(2^n (2^m +2^n ))) Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/(2^m (2^m +2^n )))=S due to symmetry Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/(2^n (2^m +2^n )))=S S=Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/2^(n+m) )−S 2S=Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((m+n+nm)/2^(n+m) )=12 S=6

$$\mathrm{Not}\:\mathrm{sure}\:\mathrm{of}\:\mathrm{the}\:\mathrm{answer}.\:\mathrm{Please}\:\mathrm{verify} \\ $$$$\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}=\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}} }\left[\frac{\mathrm{1}}{\mathrm{2}^{{m}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{2}^{{m}} }\right] \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)} \\ $$$$\:\:\:\:\:\:=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}+{m}} }−\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{m}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}=\mathrm{S} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}} \left(\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \right)}=\mathrm{S} \\ $$$$\mathrm{S}=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}+{m}} }−\mathrm{S} \\ $$$$\mathrm{2S}=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}+{n}+{nm}}{\mathrm{2}^{{n}+{m}} }=\mathrm{12} \\ $$$$\mathrm{S}=\mathrm{6} \\ $$

Commented by Yozzii last updated on 20/Dec/15

Looks correct. Thanks!

$${Looks}\:{correct}.\:{Thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com