
Question and Answers Forum
Question Number 37271 by abdo.msup.com last updated on 11/Jun/18
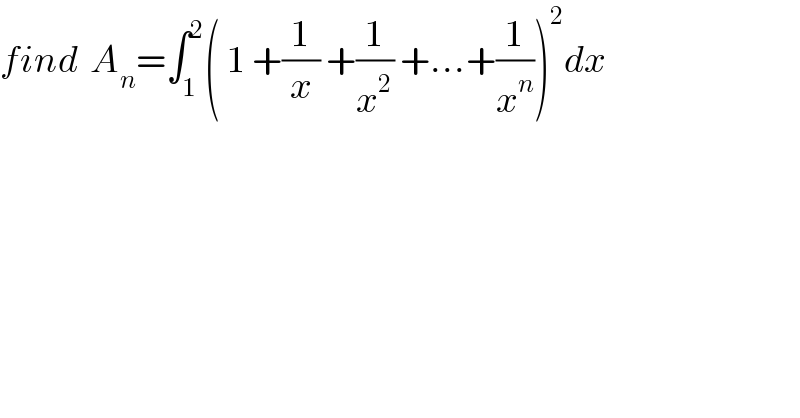
Commented by prof Abdo imad last updated on 18/Jun/18
![let a_i = (1/x^i ) with 0≤i≤n ⇒ (1+(1/x) +(1/x^2 ) +....+(1/x^n ))^2 =(Σ_(i=0) ^n a_i )^2 = Σ_(i=0) ^n a_i ^2 +2 Σ_(0≤i<j≤n) a_i .a_j =Σ_(i=0) ^n (1/x^(2i) ) +2 Σ_(0≤i<j≤n) (1/x^(i+j) ) ⇒ A_n = ∫_1 ^2 (Σ_(i=0) ^n (1/x^(2i) ))dx +2 ∫_1 ^2 Σ_(0≤i<j≤n) (1/x^(i+j) )dx =Σ_(i=0) ^n ∫_1 ^2 x^(−2i) dx +2 Σ_(0≤i<j≤n) ∫_1 ^2 x^(−(i+j)) dx Σ_(i=0) ^n (1/(−2i+1))[ x^(−2i+1) ]_1 ^2 +2 Σ_(0≤i<j≤n) (1/(1−(i+j)))[ x^(1−(i+j)) ]_1 ^2 =−Σ_(i=0) ^n (1/(2i−1)){ 2^(−2i+1) −1} −Σ_(0≤i<j≤n) (1/(i+j−1)){ 2^(1−(i+j)) −1}](Q37831.png)
Commented by math khazana by abdo last updated on 18/Jun/18
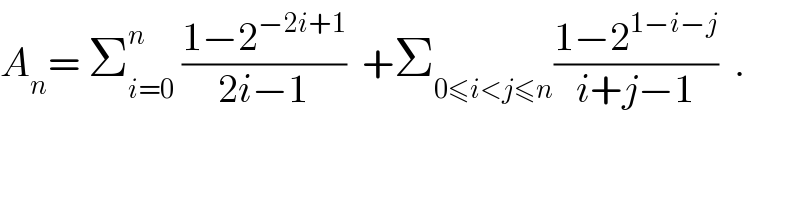
| ||
Question and Answers Forum | ||
Question Number 37271 by abdo.msup.com last updated on 11/Jun/18 | ||
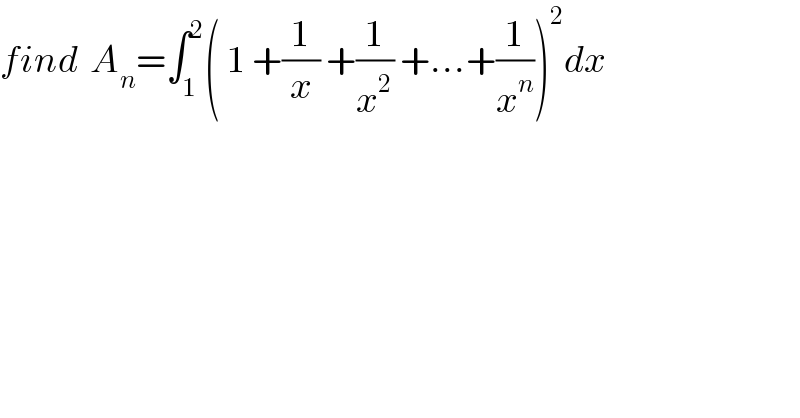 | ||
Commented by prof Abdo imad last updated on 18/Jun/18 | ||
![let a_i = (1/x^i ) with 0≤i≤n ⇒ (1+(1/x) +(1/x^2 ) +....+(1/x^n ))^2 =(Σ_(i=0) ^n a_i )^2 = Σ_(i=0) ^n a_i ^2 +2 Σ_(0≤i<j≤n) a_i .a_j =Σ_(i=0) ^n (1/x^(2i) ) +2 Σ_(0≤i<j≤n) (1/x^(i+j) ) ⇒ A_n = ∫_1 ^2 (Σ_(i=0) ^n (1/x^(2i) ))dx +2 ∫_1 ^2 Σ_(0≤i<j≤n) (1/x^(i+j) )dx =Σ_(i=0) ^n ∫_1 ^2 x^(−2i) dx +2 Σ_(0≤i<j≤n) ∫_1 ^2 x^(−(i+j)) dx Σ_(i=0) ^n (1/(−2i+1))[ x^(−2i+1) ]_1 ^2 +2 Σ_(0≤i<j≤n) (1/(1−(i+j)))[ x^(1−(i+j)) ]_1 ^2 =−Σ_(i=0) ^n (1/(2i−1)){ 2^(−2i+1) −1} −Σ_(0≤i<j≤n) (1/(i+j−1)){ 2^(1−(i+j)) −1}](Q37831.png) | ||
Commented by math khazana by abdo last updated on 18/Jun/18 | ||
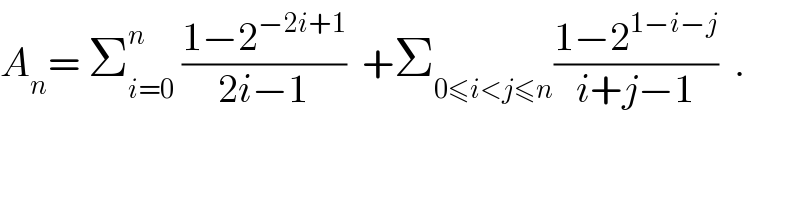 | ||