Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 37277 by abdo.msup.com last updated on 11/Jun/18

let f(x) = (1/(1+x^n )) with n integr 1)find f^′ (x) and f^(′′) (x) 2) find the poles of f 3)calculate f^((n)) (0) 4) developp f at integr serie.

$${let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:\:{with}\:{n}\:{integr} \\ $$$$\left.\mathrm{1}\right){find}\:{f}^{'} \left({x}\right)\:{and}\:{f}^{''} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{poles}\:{of}\:{f} \\ $$$$\left.\mathrm{3}\right){calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{4}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$

Commented by prof Abdo imad last updated on 16/Jun/18

1)f^′ (x)=−((nx^(n−1) )/((1+x^n )^2 )) and f^(′′) (x)=−((n(n−1)x^(n−2) (1+x^n )^2 −2(1+x^n )nx^(n−1) nx^(n−1) )/((1+x^n )^4 )) =−((n(n−1)x^(n−2) (1+x^n )−2n^2 x^(2n−2) )/((1+x^n )^3 )) 2)z^n +1=0 ⇔ z^n =e^(iπ) so if z=re^(iθ) we get r=1 and nθ=(2k+1)π ⇒θ_k =(((2k+1)π)/n) so the poles of f are z_k =e^(i(((2k+1)π)/n)) and k ∈[[0,n−1]].

$$\left.\mathrm{1}\right){f}^{'} \left({x}\right)=−\frac{{nx}^{{n}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{2}} }\:{and} \\ $$$${f}^{''} \left({x}\right)=−\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{1}+{x}^{{n}} \right){nx}^{{n}−\mathrm{1}} {nx}^{{n}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{4}} } \\ $$$$=−\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \left(\mathrm{1}+{x}^{{n}} \right)−\mathrm{2}{n}^{\mathrm{2}} \:{x}^{\mathrm{2}{n}−\mathrm{2}} }{\left(\mathrm{1}+{x}^{{n}} \right)^{\mathrm{3}} } \\ $$$$\left.\mathrm{2}\right){z}^{{n}} \:+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{z}^{{n}} ={e}^{{i}\pi} \:\:{so}\:{if}\:{z}={re}^{{i}\theta} \:{we}\:{get} \\ $$$${r}=\mathrm{1}\:{and}\:{n}\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta_{{k}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}} \\ $$$${so}\:{the}\:{poles}\:{of}\:{f}\:{are}\:{z}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \\ $$$${and}\:{k}\:\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]. \\ $$$$ \\ $$

Commented by prof Abdo imad last updated on 16/Jun/18

3) f(x)=Σ_(k=0) ^(n−1) (λ_k /(x−z_k )) λ_k = (1/(n z_k ^(n−1) )) =−(z_k /n) ⇒f(x)=−(1/n)Σ_(k=0) ^(n−1) (z_k /(x−z_k )) ⇒ f^((p)) (x) =−(1/n)Σ_(k=0) ^(n−1) z_k ( (((−1)^p p!)/((x−z_k )^(p+1) ))) =((p!(−1)^(p+1) )/n) Σ_(k=0) ^(n−1) (z_k /((x−z_k )^(p+1) )) ⇒ f^((p)) (0)= ((p!(−1)^(p+1) )/n) Σ_(k=0) ^(n−1) (z_k /((−1)^(p+1) z_k ^(p+1) )) =((p!)/n) Σ_(k=0) ^(n−1) z_k ^(−p) .

$$\left.\mathrm{3}\right)\:{f}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\lambda_{{k}} }{{x}−{z}_{{k}} } \\ $$$$\lambda_{{k}} =\:\frac{\mathrm{1}}{{n}\:{z}_{{k}} ^{{n}−\mathrm{1}} }\:=−\frac{{z}_{{k}} }{{n}}\:\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{{z}_{{k}} }{{x}−{z}_{{k}} }\:\Rightarrow \\ $$$${f}^{\left({p}\right)} \left({x}\right)\:=−\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{{k}} \left(\:\:\frac{\left(−\mathrm{1}\right)^{{p}} {p}!}{\left({x}−{z}_{{k}} \right)^{{p}+\mathrm{1}} }\right) \\ $$$$=\frac{{p}!\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} }{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{z}_{{k}} }{\left({x}−{z}_{{k}} \right)^{{p}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}^{\left({p}\right)} \left(\mathrm{0}\right)=\:\frac{{p}!\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} }{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{z}_{{k}} }{\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} \:{z}_{{k}} ^{{p}+\mathrm{1}} } \\ $$$$=\frac{{p}!}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{z}_{{k}} ^{−{p}} \:. \\ $$$$ \\ $$$$ \\ $$

Commented by prof Abdo imad last updated on 16/Jun/18

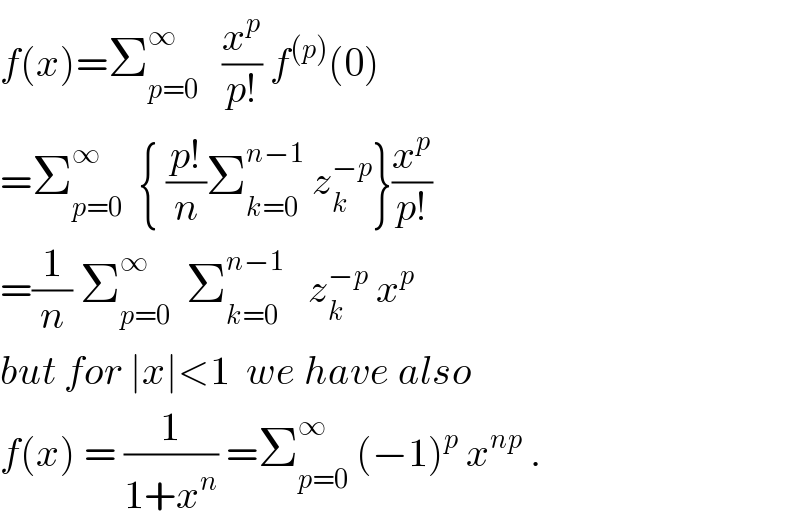
f(x)=Σ_(p=0) ^∞ (x^p /(p!)) f^((p)) (0) =Σ_(p=0) ^∞ { ((p!)/n)Σ_(k=0) ^(n−1) z_k ^(−p) }(x^p /(p!)) =(1/n) Σ_(p=0) ^∞ Σ_(k=0) ^(n−1) z_k ^(−p) x^p but for ∣x∣<1 we have also f(x) = (1/(1+x^n )) =Σ_(p=0) ^∞ (−1)^p x^(np) .

$${f}\left({x}\right)=\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{{p}} }{{p}!}\:{f}^{\left({p}\right)} \left(\mathrm{0}\right) \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\left\{\:\frac{{p}!}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{{k}} ^{−{p}} \right\}\frac{{x}^{{p}} }{{p}!} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:{z}_{{k}} ^{−{p}} \:{x}^{{p}} \\ $$$${but}\:{for}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\:{also} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:=\sum_{{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{p}} \:{x}^{{np}} \:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com