Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37285 by math khazana by abdo last updated on 11/Jun/18

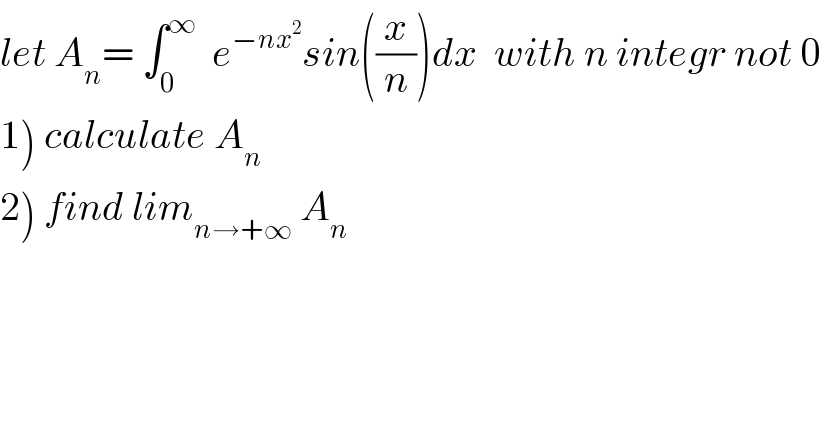
let A_n = ∫_0 ^∞ e^(−nx^2 ) sin((x/n))dx with n integr not 0 1) calculate A_n 2) find lim_(n→+∞) A_n

$${let}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nx}^{\mathrm{2}} } {sin}\left(\frac{{x}}{{n}}\right){dx}\:\:{with}\:{n}\:{integr}\:{not}\:\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$

Commented by math khazana by abdo last updated on 14/Jun/18

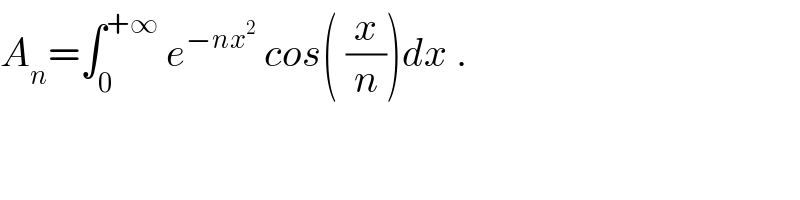
A_n =∫_0 ^(+∞) e^(−nx^2 ) cos( (x/n))dx .

$${A}_{{n}} =\int_{\mathrm{0}} ^{+\infty} \:{e}^{−{nx}^{\mathrm{2}} } \:{cos}\left(\:\frac{{x}}{{n}}\right){dx}\:. \\ $$

Commented by prof Abdo imad last updated on 16/Jun/18

changement (x/n)=t give A_n = ∫_0 ^∞ e^(−nn^2 t^2 ) cos(t) ndt =n ∫_0 ^∞ e^(−n^3 t^2 ) cost dt =(n/2) ∫_(−∞) ^(+∞) e^(−n^3 t^2 +it) dt (2/n) A_n = ∫_(−∞) ^(+∞) e^(−{(n(√n)t)^2 −it}) dt =∫_(−∞) ^(+∞) e^(−{ (n(√n)t)^2 −2 (i/(n(√n)))(n(√n)t) + ((i/(n(√n))))^2 −((i/(n(√n))))^2 }) dt = ∫_(−∞) ^(+∞) e^(−(n(√n) t −(i/(n(√n))))^2 −(1/n^3 )) dt =_(n(√n)t −(i/(n(√n))) = u) e^(−(1/n^3 )) ∫_(−∞) ^(+∞) e^(−u^2 ) du = (√π) e^(−(1/(n^3 ))) ⇒ A_n =((n(√π))/2) e^(−(1/(n^3 ))) .

$${changement}\:\frac{{x}}{{n}}={t}\:{give} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nn}^{\mathrm{2}} {t}^{\mathrm{2}} } \:{cos}\left({t}\right)\:{ndt} \\ $$$$={n}\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−{n}^{\mathrm{3}} {t}^{\mathrm{2}} } \:{cost}\:{dt} \\ $$$$=\frac{{n}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{n}^{\mathrm{3}} {t}^{\mathrm{2}} \:+{it}} {dt} \\ $$$$\frac{\mathrm{2}}{{n}}\:{A}_{{n}} =\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left\{\left({n}\sqrt{{n}}{t}\right)^{\mathrm{2}} −{it}\right\}} {dt} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\:{e}^{−\left\{\:\left({n}\sqrt{{n}}{t}\right)^{\mathrm{2}} \:−\mathrm{2}\:\frac{{i}}{{n}\sqrt{{n}}}\left({n}\sqrt{{n}}{t}\right)\:+\:\left(\frac{{i}}{{n}\sqrt{{n}}}\right)^{\mathrm{2}} \:−\left(\frac{{i}}{{n}\sqrt{{n}}}\right)^{\mathrm{2}} \right\}} {dt} \\ $$$$=\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−\left({n}\sqrt{{n}}\:{t}\:−\frac{{i}}{{n}\sqrt{{n}}}\right)^{\mathrm{2}} \:\:−\frac{\mathrm{1}}{{n}^{\mathrm{3}} }} \:{dt} \\ $$$$=_{{n}\sqrt{{n}}{t}\:−\frac{{i}}{{n}\sqrt{{n}}}\:=\:{u}} {e}^{−\frac{\mathrm{1}}{{n}^{\mathrm{3}} }} \:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−{u}^{\mathrm{2}} } \:{du} \\ $$$$=\:\sqrt{\pi}\:\:{e}^{−\frac{\mathrm{1}}{{n}^{\mathrm{3}} \:\:}} \:\:\Rightarrow \\ $$$${A}_{{n}} =\frac{{n}\sqrt{\pi}}{\mathrm{2}}\:{e}^{−\frac{\mathrm{1}}{{n}^{\mathrm{3}} \:\:}} \:\:\:. \\ $$

Commented by math khazana by abdo last updated on 17/Jun/18

2) its clear that lim_(n→+∞) A_n =+∞ .

$$\left.\mathrm{2}\right)\:{its}\:{clear}\:{that}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \:=+\infty\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com