Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37288 by math khazana by abdo last updated on 11/Jun/18

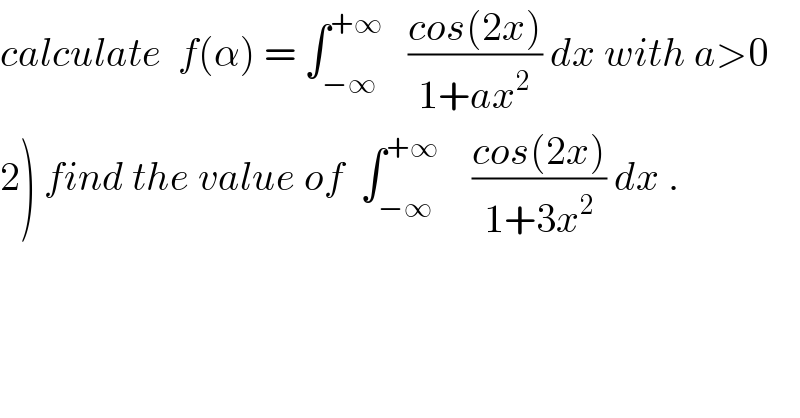
calculate f(α) = ∫_(−∞) ^(+∞) ((cos(2x))/(1+ax^2 )) dx with a>0 2) find the value of ∫_(−∞) ^(+∞) ((cos(2x))/(1+3x^2 )) dx .

$${calculate}\:\:{f}\left(\alpha\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{ax}^{\mathrm{2}} }\:{dx}\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:. \\ $$

Commented byprof Abdo imad last updated on 16/Jun/18

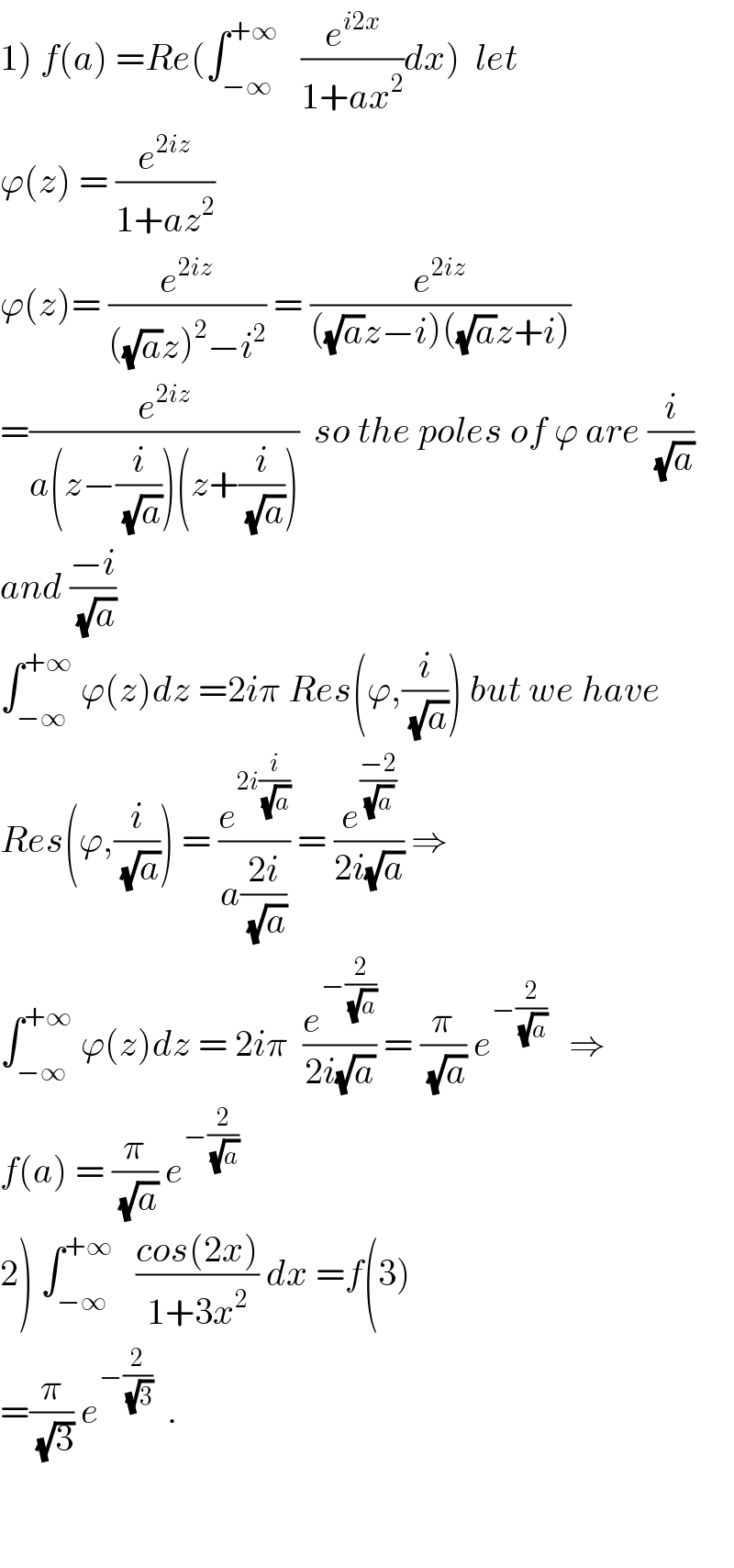
1) f(a) =Re(∫_(−∞) ^(+∞) (e^(i2x) /(1+ax^2 ))dx) let ϕ(z) = (e^(2iz) /(1+az^2 )) ϕ(z)= (e^(2iz) /(((√a)z)^2 −i^2 )) = (e^(2iz) /(((√a)z−i)((√a)z+i))) =(e^(2iz) /(a(z−(i/(√a)))(z+(i/(√a))))) so the poles of ϕ are (i/(√a)) and ((−i)/(√a)) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,(i/(√a))) but we have Res(ϕ,(i/(√a))) = (e^(2i(i/(√a))) /(a((2i)/(√a)))) = (e^((−2)/(√a)) /(2i(√a))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz = 2iπ (e^(−(2/(√a))) /(2i(√a))) = (π/(√a)) e^(−(2/(√a))) ⇒ f(a) = (π/(√a)) e^(−(2/(√a))) 2) ∫_(−∞) ^(+∞) ((cos(2x))/(1+3x^2 )) dx =f(3) =(π/(√3)) e^(−(2/(√3))) .

$$\left.\mathrm{1}\right)\:{f}\left({a}\right)\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{{i}\mathrm{2}{x}} }{\mathrm{1}+{ax}^{\mathrm{2}} }{dx}\right)\:\:{let}\: \\ $$ $$\varphi\left({z}\right)\:=\:\frac{{e}^{\mathrm{2}{iz}} }{\mathrm{1}+{az}^{\mathrm{2}} } \\ $$ $$\varphi\left({z}\right)=\:\frac{{e}^{\mathrm{2}{iz}} }{\left(\sqrt{{a}}{z}\right)^{\mathrm{2}} −{i}^{\mathrm{2}} }\:=\:\frac{{e}^{\mathrm{2}{iz}} }{\left(\sqrt{{a}}{z}−{i}\right)\left(\sqrt{{a}}{z}+{i}\right)} \\ $$ $$=\frac{{e}^{\mathrm{2}{iz}} }{{a}\left({z}−\frac{{i}}{\sqrt{{a}}}\right)\left({z}+\frac{{i}}{\sqrt{{a}}}\right)}\:\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\frac{{i}}{\sqrt{{a}}} \\ $$ $${and}\:\frac{−{i}}{\sqrt{{a}}} \\ $$ $$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\frac{{i}}{\sqrt{{a}}}\right)\:{but}\:{we}\:{have} \\ $$ $${Res}\left(\varphi,\frac{{i}}{\sqrt{{a}}}\right)\:=\:\frac{{e}^{\mathrm{2}{i}\frac{{i}}{\sqrt{{a}}}} }{{a}\frac{\mathrm{2}{i}}{\sqrt{{a}}}}\:=\:\frac{{e}^{\frac{−\mathrm{2}}{\sqrt{{a}}}} }{\mathrm{2}{i}\sqrt{{a}}}\:\Rightarrow \\ $$ $$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\:\:\frac{{e}^{−\frac{\mathrm{2}}{\sqrt{{a}}}} }{\mathrm{2}{i}\sqrt{{a}}}\:=\:\frac{\pi}{\sqrt{{a}}}\:{e}^{−\frac{\mathrm{2}}{\sqrt{{a}}}} \:\:\:\Rightarrow \\ $$ $${f}\left({a}\right)\:=\:\frac{\pi}{\sqrt{{a}}}\:{e}^{−\frac{\mathrm{2}}{\sqrt{{a}}}} \\ $$ $$\left.\mathrm{2}\right)\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:={f}\left(\mathrm{3}\right) \\ $$ $$=\frac{\pi}{\sqrt{\mathrm{3}}}\:{e}^{−\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}} \:\:. \\ $$ $$ \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com