Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37317 by rahul 19 last updated on 11/Jun/18

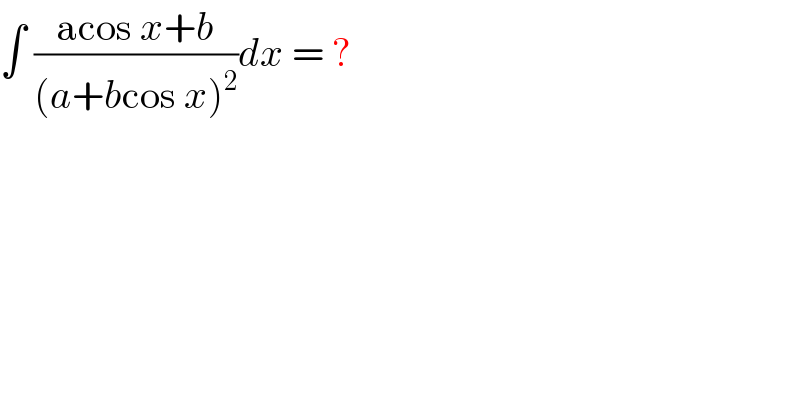
∫ ((acos x+b)/((a+bcos x)^2 ))dx = ?

$$\int\:\frac{\mathrm{acos}\:{x}+{b}}{\left({a}+{b}\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}\:=\:? \\ $$

Commented by math khazana by abdo last updated on 12/Jun/18

changement tan((x/2)) = t give I = ∫ ((a((1−t^2 )/(1+t^2 )) +b)/((a +b((1−t^2 )/(1+t^2 )))^2 )) ((2dt)/(1+t^2 )) =2 ∫ ((a(1−t^2 ) +b +bt^2 )/((1+t^2 )^2 (((a+at^2 +b−bt^2 )^2 )/((1+t^2 )^2 )))) dt = 2 ∫ ((a+b +(b−a)t^2 )/({a+b +(a−b)t^2 }^2 )) dt case 1 a>b I =2 ∫ (((a+b){ 1−(a−b)t^2 })/((a+b)^2 { 1+((a−b)/(a+b))t^2 }^2 )) dt =(2/(a+b)) ∫ ((1−((a−b)/(a+b))t^2 )/({1 +((a−b)/(a+b))t^2 }^2 ))dt changement (√((a−b)/(a+b)))t =x give I = (2/(a+b)) ∫ ((1−x^2 )/({1+x^2 }^2 )) (√((a+b)/(a−b))) dx = (2/(√(a^2 −b^2 ))) ∫ ((1−x^2 )/((1+x^2 )^2 )) dx but ∫ ((1−x^2 )/((1+x^2 )^2 ))dx = ∫ ((1+x^2 −2x^2 )/((1+x^2 )^2 ))dx = ∫ (dx/(1+x^2 )) −∫ ((2x^2 )/((1+x^2 )^2 ))dx =arctanx −∫ ((2x^2 )/((1+x^2 )^2 ))dx by parts u^′ = ((−2x)/((1+x^2 )^2 )) and u =x ∫ ((−2x)/((1+x^2 )^2 )) x dx = (1/(1+x^2 )) x −∫ (1/(1+x^2 )) dx =(x/(1+x^2 )) −arctan(x) ⇒ I = (2/(√(a^2 −b^2 ))){ arctan(x) +(x/(1+x^2 )) −arctan(x)} +c I = ((2x)/((√(a^2 −b^2 ))(1+x^2 )))

$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:=\:{t}\:{give}\: \\ $$$${I}\:=\:\int\:\:\frac{{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+{b}}{\left({a}\:+{b}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{{a}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\:\:+{b}\:+{bt}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \frac{\left({a}+{at}^{\mathrm{2}} \:+{b}−{bt}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:{dt} \\ $$$$=\:\mathrm{2}\:\int\:\:\:\:\:\:\frac{{a}+{b}\:+\left({b}−{a}\right){t}^{\mathrm{2}} }{\left\{{a}+{b}\:\:+\left({a}−{b}\right){t}^{\mathrm{2}} \right\}^{\mathrm{2}} }\:{dt} \\ $$$${case}\:\mathrm{1}\:\:{a}>{b}\:\: \\ $$$${I}\:\:=\mathrm{2}\:\:\int\:\:\frac{\left({a}+{b}\right)\left\{\:\mathrm{1}−\left({a}−{b}\right){t}^{\mathrm{2}} \right\}}{\left({a}+{b}\right)^{\mathrm{2}} \left\{\:\:\mathrm{1}+\frac{{a}−{b}}{{a}+{b}}{t}^{\mathrm{2}} \right\}^{\mathrm{2}} }\:{dt} \\ $$$$=\frac{\mathrm{2}}{{a}+{b}}\:\int\:\:\:\:\:\frac{\mathrm{1}−\frac{{a}−{b}}{{a}+{b}}{t}^{\mathrm{2}} }{\left\{\mathrm{1}\:+\frac{{a}−{b}}{{a}+{b}}{t}^{\mathrm{2}} \right\}^{\mathrm{2}} }{dt}\:\:{changement} \\ $$$$\sqrt{\frac{{a}−{b}}{{a}+{b}}}{t}\:={x}\:{give} \\ $$$${I}\:\:=\:\frac{\mathrm{2}}{{a}+{b}}\:\int\:\:\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left\{\mathrm{1}+{x}^{\mathrm{2}} \right\}^{\mathrm{2}} }\:\sqrt{\frac{{a}+{b}}{{a}−{b}}}\:{dx} \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }}\:\int\:\:\:\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:\:{but} \\ $$$$\int\:\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=\:\int\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} \:−\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\:\int\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:−\int\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$={arctanx}\:\:−\int\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\:{by}\:{parts} \\ $$$${u}^{'} \:\:\:\:=\:\frac{−\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{and}\:\:{u}\:={x} \\ $$$$\int\:\:\:\:\frac{−\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{x}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{x}\:\:−\int\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:−{arctan}\left({x}\right)\:\Rightarrow\: \\ $$$$\:{I}\:\:=\:\frac{\mathrm{2}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }}\left\{\:\:{arctan}\left({x}\right)\:\:+\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−{arctan}\left({x}\right)\right\}\:+{c}\: \\ $$$${I}\:=\:\:\frac{\mathrm{2}{x}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$

Commented by math khazana by abdo last updated on 12/Jun/18

case 2 a<b we get I = (2/(a+b)) ∫ ((1 +((b−a)/(b+a))t^2 )/({1−((b−a)/(b+a))t^2 }^2 )) dt and changement (√((b−a)/(b+a)))t =x give I = (2/(a+b)) (√((b+a)/(b−a))) ∫ ((1+x^2 )/((1−x^2 )^2 ))dx = (2/(√(b^2 −a^2 ))) ∫ ((1+x^2 )/((1−x^2 )^2 )) dx but ∫ ((1+x^2 )/((1−x^2 )^2 )) dx = ∫ ((1−x^2 +2x^2 )/((1−x^2 )^2 )) dx = ∫ (dx/(1−x^2 )) + ∫ ((2x)/((1−x^2 )^2 )) dx =ln∣((1+x)/(1−x))∣ + ∫ ((2x)/((1−x^2 )^2 )) dx by parts u^′ = ((2x)/((1−x^2 )^2 )) and v =x ⇒ ∫ ((2x)/((1−x^2 )^2 )) dx = (1/(1−x^2 )) x − ∫ (1/(1−x^2 )) dx = (x/(1−x^2 )) −ln∣((1+x)/(1−x))∣ ⇒ I = (2/(√(b^2 −a^2 ))){ ln∣((1+x)/(1−x))∣ +(x/(1−x^2 )) −ln∣((1+x)/(1−x))∣ I = ((2x)/((√(b^2 −a^2 ))(1−x^2 ))) +c

$${case}\:\mathrm{2}\:\:{a}<{b}\:\:{we}\:{get}\: \\ $$$${I}\:=\:\frac{\mathrm{2}}{{a}+{b}}\:\int\:\:\frac{\mathrm{1}\:+\frac{{b}−{a}}{{b}+{a}}{t}^{\mathrm{2}} }{\left\{\mathrm{1}−\frac{{b}−{a}}{{b}+{a}}{t}^{\mathrm{2}} \right\}^{\mathrm{2}} }\:{dt}\:\:{and}\:{changement} \\ $$$$\sqrt{\frac{{b}−{a}}{{b}+{a}}}{t}\:={x}\:{give}\: \\ $$$${I}\:=\:\frac{\mathrm{2}}{{a}+{b}}\:\sqrt{\frac{{b}+{a}}{{b}−{a}}}\:\int\:\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} }}\:\int\:\:\:\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:\:{but} \\ $$$$\int\:\:\:\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:=\:\int\:\frac{\mathrm{1}−{x}^{\mathrm{2}} \:+\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx} \\ $$$$=\:\int\:\:\:\:\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\:+\:\:\int\:\:\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx} \\ $$$$={ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:\:+\:\int\:\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:\:{by}\:{parts} \\ $$$${u}^{'} \:\:=\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:{and}\:{v}\:={x}\:\Rightarrow \\ $$$$\int\:\:\:\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:=\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{x}\:−\:\int\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx} \\ $$$$=\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\:−{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:\Rightarrow \\ $$$${I}\:=\:\:\frac{\mathrm{2}}{\sqrt{{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} }}\left\{\:\:{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:\:+\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:−{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\right. \\ $$$${I}\:=\:\frac{\mathrm{2}{x}}{\sqrt{{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:\:+{c} \\ $$

Commented by math khazana by abdo last updated on 12/Jun/18

I = ((2x)/((√(a^2 −b^2 ))(1+x^2 ))) +c

$${I}\:=\:\frac{\mathrm{2}{x}}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\:+{c}\: \\ $$

Commented by math khazana by abdo last updated on 12/Jun/18

x =(√((a−b)/(a+b))) tan((x/2)) at case 1 and x =(√((b−a)/(b+a))) tan((x/2)) at case 2 .

$${x}\:=\sqrt{\frac{{a}−{b}}{{a}+{b}}}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:{at}\:{case}\:\mathrm{1}\:{and}\:{x}\:=\sqrt{\frac{{b}−{a}}{{b}+{a}}}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$$${at}\:{case}\:\mathrm{2}\:. \\ $$

Answered by behi83417@gmail.com last updated on 12/Jun/18

tg(x/2)=t⇒(1+t^2 )dx=2dt,cosx=((1−t^2 )/(1+t^2 )) ⇒I=∫((a((1−t^2 )/(1+t^2 ))+b)/((a+b((1−t^2 )/(1+t^2 )))^2 )).((2dt)/(1+t^2 ))= =∫((a+b−(a−b)t^2 )/((a+b+(a−b)t^2 )^2 ))dt=∫((m−nt^2 )/((m+nt^2 )^2 ))dt= =(m/n^2 )∫(dt/(((m/n)+t^2 )^2 ))−(1/n)∫(t^2 /(((m/n)+t^2 )^2 ))dt=AI_1 +BI_2 1)I_1 =∫(dt/(((m/n)+t^2 )^2 ))=(n/m)∫(((m/n)+t^2 −t^2 )/(((m/n)+t^2 )^2 ))dt= =(n/m)[∫(dt/(((m/n)+t^2 )))−∫(t^2 /(((m/n)+t^2 )^2 ))dt]= =(n/m)[(√(n/m)).tg^(−1) ((t/(√(m/n))))+nI_2 ] I_2 =∫(t^2 /(((m/n)+t^2 )^2 ))dt=−(t/(2(t^2 +(m/n))))+((tg^(−1) (t/(√(m/n))))/(2(√(m/n)))) ⇒I=(m/n^2 ).I_1 −(1/n).I_2 =(m/n^2 ).(n/m)((√(n/m)).tg^(−1) ((√(n/m)).t)− −((nt)/(2(t^2 +(m/n))))+(1/2)n(√(n/m))tg^(−1) ((√(n/m))t))− −(1/n)(−(t/(2(t^2 +(m/n))))+(1/2)(√(n/m)).tg^(−1) ((√(n/m))t))= =(1/(√(mn)))tg^(−1) ((√(n/m))t)−(t/(2(t^2 +(m/n))))+(1/2)(√(n/m))tg^(−1) ((√(n/m))t)− −(t/(2n(t^2 +(m/n))))+(1/(2(√(mn))))tg^(−1) ((√(n/m))t)= =((3+n)/(2(√(mn))))tg^(−1) ((√(n/m))t)−((n+1)/n).(t/(t^2 +(m/n)))+C= =((3+a−b)/(2(√(a^2 −b^2 )))).tg^(−1) ((√((a−b)/(a+b))).tg(x/2))− −(a−b+1).((tg(x/2))/((a−b)tg^2 (x/2)+(a+b))) .■

$${tg}\frac{{x}}{\mathrm{2}}={t}\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx}=\mathrm{2}{dt},{cosx}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow{I}=\int\frac{{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+{b}}{\left({a}+{b}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }.\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }= \\ $$$$=\int\frac{{a}+{b}−\left({a}−{b}\right){t}^{\mathrm{2}} }{\left({a}+{b}+\left({a}−{b}\right){t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\int\frac{{m}−{nt}^{\mathrm{2}} }{\left({m}+{nt}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}= \\ $$$$=\frac{{m}}{{n}^{\mathrm{2}} }\int\frac{{dt}}{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}}\int\frac{{t}^{\mathrm{2}} }{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}={AI}_{\mathrm{1}} +{BI}_{\mathrm{2}} \\ $$$$\left.\mathrm{1}\right){I}_{\mathrm{1}} =\int\frac{{dt}}{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{{n}}{{m}}\int\frac{\frac{{m}}{{n}}+{t}^{\mathrm{2}} −{t}^{\mathrm{2}} }{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}= \\ $$$$=\frac{{n}}{{m}}\left[\int\frac{{dt}}{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)}−\int\frac{{t}^{\mathrm{2}} }{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\right]= \\ $$$$=\frac{{n}}{{m}}\left[\sqrt{\frac{{n}}{{m}}}.{tg}^{−\mathrm{1}} \left(\frac{{t}}{\sqrt{\frac{{m}}{{n}}}}\right)+{nI}_{\mathrm{2}} \right] \\ $$$${I}_{\mathrm{2}} =\int\frac{{t}^{\mathrm{2}} }{\left(\frac{{m}}{{n}}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} +\frac{{m}}{{n}}\right)}+\frac{{tg}^{−\mathrm{1}} \frac{{t}}{\sqrt{\frac{{m}}{{n}}}}}{\mathrm{2}\sqrt{\frac{{m}}{{n}}}} \\ $$$$\Rightarrow{I}=\frac{{m}}{{n}^{\mathrm{2}} }.{I}_{\mathrm{1}} −\frac{\mathrm{1}}{{n}}.{I}_{\mathrm{2}} =\frac{{m}}{{n}^{\mathrm{2}} }.\frac{{n}}{{m}}\left(\sqrt{\frac{{n}}{{m}}}.{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}.{t}\right)−\right. \\ $$$$\left.−\frac{{nt}}{\mathrm{2}\left({t}^{\mathrm{2}} +\frac{{m}}{{n}}\right)}+\frac{\mathrm{1}}{\mathrm{2}}{n}\sqrt{\frac{{n}}{{m}}}{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)\right)− \\ $$$$−\frac{\mathrm{1}}{{n}}\left(−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} +\frac{{m}}{{n}}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{n}}{{m}}}.{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\sqrt{{mn}}}{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} +\frac{{m}}{{n}}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{n}}{{m}}}{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)− \\ $$$$−\frac{{t}}{\mathrm{2}{n}\left({t}^{\mathrm{2}} +\frac{{m}}{{n}}\right)}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{mn}}}{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)= \\ $$$$=\frac{\mathrm{3}+{n}}{\mathrm{2}\sqrt{{mn}}}{tg}^{−\mathrm{1}} \left(\sqrt{\frac{{n}}{{m}}}{t}\right)−\frac{{n}+\mathrm{1}}{{n}}.\frac{{t}}{{t}^{\mathrm{2}} +\frac{{m}}{{n}}}+{C}= \\ $$$$=\frac{\mathrm{3}+\boldsymbol{{a}}−\boldsymbol{{b}}}{\mathrm{2}\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} }}.\boldsymbol{{tg}}^{−\mathrm{1}} \left(\sqrt{\frac{\boldsymbol{{a}}−\boldsymbol{{b}}}{\boldsymbol{{a}}+\boldsymbol{{b}}}}.\boldsymbol{{tg}}\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)− \\ $$$$−\left(\boldsymbol{{a}}−\boldsymbol{{b}}+\mathrm{1}\right).\frac{\boldsymbol{{tg}}\frac{\boldsymbol{{x}}}{\mathrm{2}}}{\left(\boldsymbol{{a}}−\boldsymbol{{b}}\right)\boldsymbol{{tg}}^{\mathrm{2}} \frac{\boldsymbol{{x}}}{\mathrm{2}}+\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)}\:.\blacksquare \\ $$

Answered by rahul 19 last updated on 13/Jun/18

Guys i gave this problem just to realise that a short trick exists in this form. Just multiplying and dividing by cosec^2 x will suffice.

$$\mathrm{Guys}\:\mathrm{i}\:\mathrm{gave}\:\mathrm{this}\:\mathrm{problem}\:\mathrm{just}\:\mathrm{to}\:\mathrm{realise} \\ $$$$\mathrm{that}\:\mathrm{a}\:\mathrm{short}\:\mathrm{trick}\:\mathrm{exists}\:\mathrm{in}\:\mathrm{this}\:\mathrm{form}. \\ $$$$\mathrm{Just}\:\mathrm{multiplying}\:\mathrm{and}\:\mathrm{dividing}\:\mathrm{by} \\ $$$$\mathrm{cosec}^{\mathrm{2}} {x}\:{will}\:{suffice}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com