
Previous in Relation and Functions Next in Relation and Functions
Question Number 37333 by math khazana by abdo last updated on 12/Jun/18
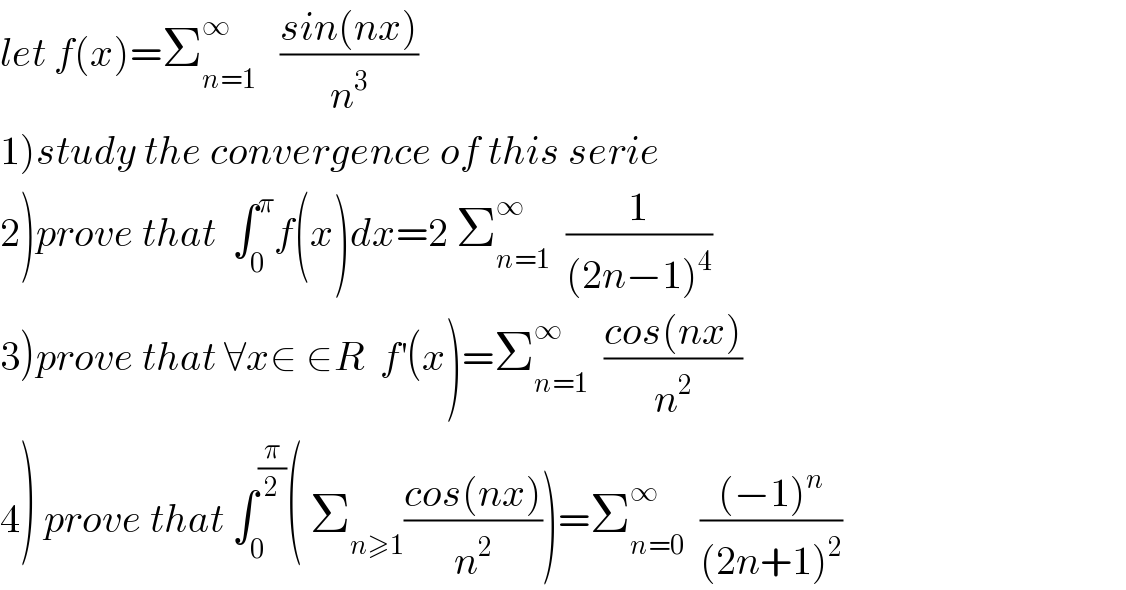
$${let}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} } \\ $$$$\left.\mathrm{1}\right){study}\:{the}\:{convergence}\:{of}\:{this}\:{serie} \\ $$$$\left.\mathrm{2}\right){prove}\:{that}\:\:\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){dx}=\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{3}\right){prove}\:{that}\:\forall{x}\in\:\in{R}\:\:{f}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right)\:{prove}\:{that}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\sum_{{n}\geqslant\mathrm{1}} \frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by prof Abdo imad last updated on 17/Jun/18
![1) the uniform convergence of this serie is assured because ∀x∈R ∣((sin(nx))/n^3 )∣≤(1/n^3 ) and Σ (1/n^3 ) is comvergent 2) ∫_0 ^π f(x)dx= ∫_0 ^π Σ_(n=1) ^∞ ((sin(nx))/n^3 )dx =Σ_(n=1) ^∞ (1/n^3 ) ∫_0 ^π sin(nx)dx but ∫_0 ^π sin(nx)dx= [−(1/n)cos(nx)]_0 ^π =(1/n)(1−(−1)^n ) ⇒∫_0 ^π f(x)dx^ =Σ_(n=1) ^∞ (1/n^4 )(1−(−1)^n ) =2 Σ_(n=0) ^∞ (1/((2n+1)^4 )) =_(n+1=p) 2Σ_(p=1) ^∞ (1/((2p−1)^4 ))](Q37761.png)
$$\left.\mathrm{1}\right)\:{the}\:{uniform}\:{convergence}\:{of}\:{this}\:{serie}\:{is} \\ $$$${assured}\:{because}\:\forall{x}\in{R}\:\mid\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }\mid\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:{and} \\ $$$$\Sigma\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:{is}\:{comvergent} \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\pi} \:{f}\left({x}\right){dx}=\:\int_{\mathrm{0}} ^{\pi} \sum_{{n}=\mathrm{1}} ^{\infty} \frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }{dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{\pi} \:\:{sin}\left({nx}\right){dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:{sin}\left({nx}\right){dx}=\:\left[−\frac{\mathrm{1}}{{n}}{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} =\frac{\mathrm{1}}{{n}}\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \:{f}\left({x}\right){d}\overset{} {{x}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right) \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} }\:=_{{n}+\mathrm{1}={p}} \:\mathrm{2}\sum_{{p}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$
Commented by prof Abdo imad last updated on 17/Jun/18
![3)let f_n (x)= ((sin(nx))/n^3 ) we have Σ f_n c.unif. and Σ f_n ^′ conv.unif. ⇒f^′ (x)=Σ f_n ^′ (x) =Σ_(n=1) ^∞ ((ncos(nx))/n^3 ) =Σ_(n=1) ^∞ ((cos(nx))/n^2 ) 4) due to uniform conv. we have also ∫_0 ^(π/2) (Σ_(n=1) ^∞ ((cos(nx))/n^2 ))=Σ_(n=1) ^∞ (1/n^2 )∫_0 ^(π/2) cos(nx)dx =Σ_(n=1) ^∞ (1/n^2 )[(1/n)sin(nx)]_0 ^(π/2) =Σ_(n=1) ^∞ (1/n^3 )sin(n(π/2))=Σ_(n=0) ^∞ (1/((2n+1)^3 ))sin((2n+1)(π/2)) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) .](Q37762.png)
$$\left.\mathrm{3}\right){let}\:{f}_{{n}} \left({x}\right)=\:\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{3}} }\:\:{we}\:{have}\:\Sigma\:{f}_{{n}} {c}.{unif}. \\ $$$${and}\:\Sigma\:{f}_{{n}} ^{'} \:\:{conv}.{unif}.\:\:\Rightarrow{f}^{'} \left({x}\right)=\Sigma\:{f}_{{n}} ^{'} \left({x}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{ncos}\left({nx}\right)}{{n}^{\mathrm{3}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right)\:{due}\:{to}\:{uniform}\:{conv}.\:{we}\:{have}\:{also} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left({nx}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left[\frac{\mathrm{1}}{{n}}{sin}\left({nx}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }{sin}\left({n}\frac{\pi}{\mathrm{2}}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }{sin}\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\:. \\ $$
