Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37349 by math khazana by abdo last updated on 12/Jun/18

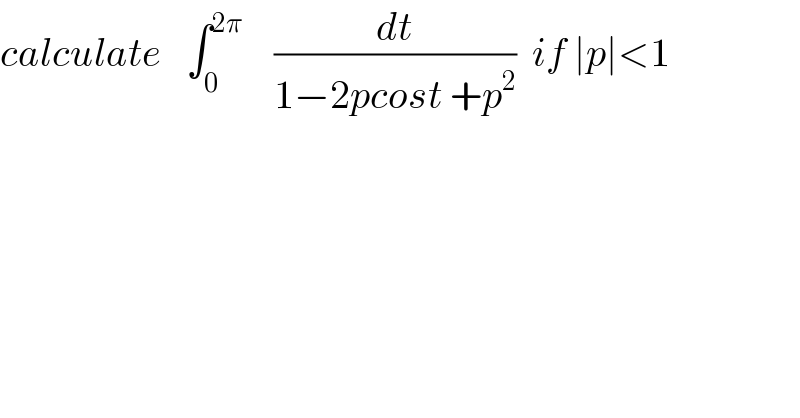
calculate ∫_0 ^(2π) (dt/(1−2pcost +p^2 )) if ∣p∣<1

$${calculate}\:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{{dt}}{\mathrm{1}−\mathrm{2}{pcost}\:+{p}^{\mathrm{2}} }\:\:{if}\:\mid{p}\mid<\mathrm{1} \\ $$

Commented bymath khazana by abdo last updated on 13/Jun/18

changement e^(it) =z give I = ∫_(∣z∣=1) (1/(1−2p ((z+z^(−1) )/2) +p^2 )) (dz/(iz)) = ∫_(∣z∣=1) ((−idz)/(z(1+p^2 −pz −pz^(−1) ))) =∫_(∣z∣ =1) ((−idz)/((1+p^2 )z −pz^2 −p)) = ∫_(∣z∣=1) ((idz)/(pz^2 −(1+p^2 )z +p)) let consider the complex function ϕ(z) = (i/(pz^2 −(1+p^2 )z +p)) poles of ϕ? Δ =(1+p^2 )^2 −4p^2 = 1 +2p^2 +p^4 −4p^2 =p^4 +1−2p^2 =(p^2 −1)^2 z_1 = ((1+p^2 +∣p^2 −1∣)/(2p)) = ((1+p^2 +1−p^2 )/(2p)) =(1/p) z_2 =((1+p^2 −∣p^2 −1∣)/(2p)) =((1+p^2 −1+p^2 )/(2p)) =p ∣z_1 ∣= (1/(∣p∣)) >1 because ∣p∣<1 and?we suppose that p≠0 ∣z_2 ∣ =∣p∣<1 so ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_2 ) but we have ϕ(z)= (i/(p(z−z_1 )(z−z_2 ))) ⇒ Res(ϕ,z_2 ) =lim_(z→z_2 ) (z−z_2 )ϕ(z) = (i/(p(z_2 −z_1 ))) = (i/(p(p−(1/p)))) = (i/((p^2 −1))) ⇒ ∫_(∣z∣=1) ϕ(z)dz = 2iπ (i/(p^2 −1)) =((−2π)/(p^2 −1)) =((2π)/(1−p^2 )) I = ((2π)/(1−p^2 )) if p=0 I = ∫_0 ^(2π) dt =2π .

$${changement}\:{e}^{{it}} \:={z}\:{give}\: \\ $$ $${I}\:\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}{p}\:\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\:+{p}^{\mathrm{2}} }\:\frac{{dz}}{{iz}} \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{−{idz}}{{z}\left(\mathrm{1}+{p}^{\mathrm{2}} \:−{pz}\:−{pz}^{−\mathrm{1}} \right)} \\ $$ $$=\int_{\mid{z}\mid\:=\mathrm{1}} \:\:\:\:\:\frac{−{idz}}{\left(\mathrm{1}+{p}^{\mathrm{2}} \right){z}\:−{pz}^{\mathrm{2}} \:−{p}}\: \\ $$ $$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{{idz}}{{pz}^{\mathrm{2}} \:−\left(\mathrm{1}+{p}^{\mathrm{2}} \right){z}\:+{p}}\:\:{let}\:{consider}\:{the} \\ $$ $${complex}\:{function}\:\varphi\left({z}\right)\:=\:\frac{{i}}{{pz}^{\mathrm{2}} \:−\left(\mathrm{1}+{p}^{\mathrm{2}} \right){z}\:+{p}} \\ $$ $${poles}\:{of}\:\varphi? \\ $$ $$\Delta\:=\left(\mathrm{1}+{p}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{4}{p}^{\mathrm{2}} \:=\:\mathrm{1}\:+\mathrm{2}{p}^{\mathrm{2}} \:+{p}^{\mathrm{4}} \:−\mathrm{4}{p}^{\mathrm{2}} \\ $$ $$={p}^{\mathrm{4}} \:+\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \:=\left({p}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$ $${z}_{\mathrm{1}} =\:\frac{\mathrm{1}+{p}^{\mathrm{2}} \:+\mid{p}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2}{p}}\:=\:\frac{\mathrm{1}+{p}^{\mathrm{2}} \:+\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{2}{p}}\:=\frac{\mathrm{1}}{{p}} \\ $$ $${z}_{\mathrm{2}} =\frac{\mathrm{1}+{p}^{\mathrm{2}} −\mid{p}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2}{p}}\:=\frac{\mathrm{1}+{p}^{\mathrm{2}} \:−\mathrm{1}+{p}^{\mathrm{2}} }{\mathrm{2}{p}}\:={p} \\ $$ $$\mid{z}_{\mathrm{1}} \mid=\:\frac{\mathrm{1}}{\mid{p}\mid}\:>\mathrm{1}\:\:{because}\:\mid{p}\mid<\mathrm{1}\:{and}?{we}\:{suppose}\:{that} \\ $$ $${p}\neq\mathrm{0} \\ $$ $$\mid{z}_{\mathrm{2}} \mid\:=\mid{p}\mid<\mathrm{1}\:\:{so} \\ $$ $$\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:\:{but}\:{we}\:{have} \\ $$ $$\varphi\left({z}\right)=\:\:\frac{{i}}{{p}\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\Rightarrow \\ $$ $${Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:={lim}_{{z}\rightarrow{z}_{\mathrm{2}} } \left({z}−{z}_{\mathrm{2}} \right)\varphi\left({z}\right) \\ $$ $$=\:\frac{{i}}{{p}\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)}\:=\:\frac{{i}}{{p}\left({p}−\frac{\mathrm{1}}{{p}}\right)}\:=\:\frac{{i}}{\left({p}^{\mathrm{2}} −\mathrm{1}\right)}\:\Rightarrow \\ $$ $$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\:\frac{{i}}{{p}^{\mathrm{2}} −\mathrm{1}}\:=\frac{−\mathrm{2}\pi}{{p}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{2}\pi}{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$ $${I}\:=\:\frac{\mathrm{2}\pi}{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$ $${if}\:{p}=\mathrm{0}\:\:{I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:{dt}\:=\mathrm{2}\pi\:. \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com