Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3735 by prakash jain last updated on 19/Dec/15

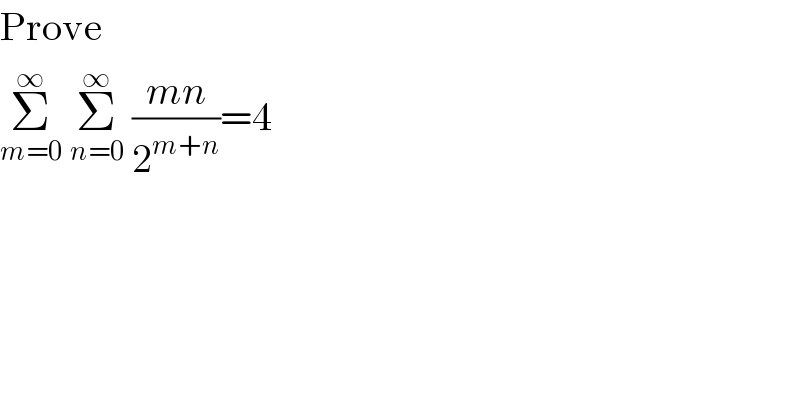
Prove Σ_(m=0) ^∞ Σ_(n=0) ^∞ ((mn)/2^(m+n) )=4

$$\mathrm{Prove} \\ $$$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{mn}}{\mathrm{2}^{{m}+{n}} }=\mathrm{4} \\ $$

Commented by prakash jain last updated on 19/Dec/15

As a part answer to Q3716.

$$\mathrm{As}\:\mathrm{a}\:\mathrm{part}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{Q3716}. \\ $$

Answered by prakash jain last updated on 19/Dec/15

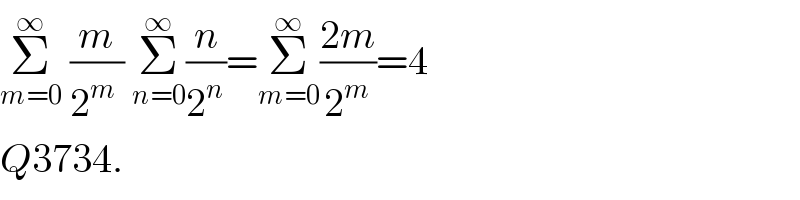
Σ_(m=0) ^∞ (m/(2^m )) Σ_(n=0) ^∞ (n/2^n )=Σ_(m=0) ^∞ ((2m)/2^m )=4 Q3734.

$$\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{m}}{\mathrm{2}^{{m}} \:}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{2}^{{n}} }=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{m}}{\mathrm{2}^{{m}} }=\mathrm{4} \\ $$$${Q}\mathrm{3734}. \\ $$

Commented by Yozzii last updated on 19/Dec/15

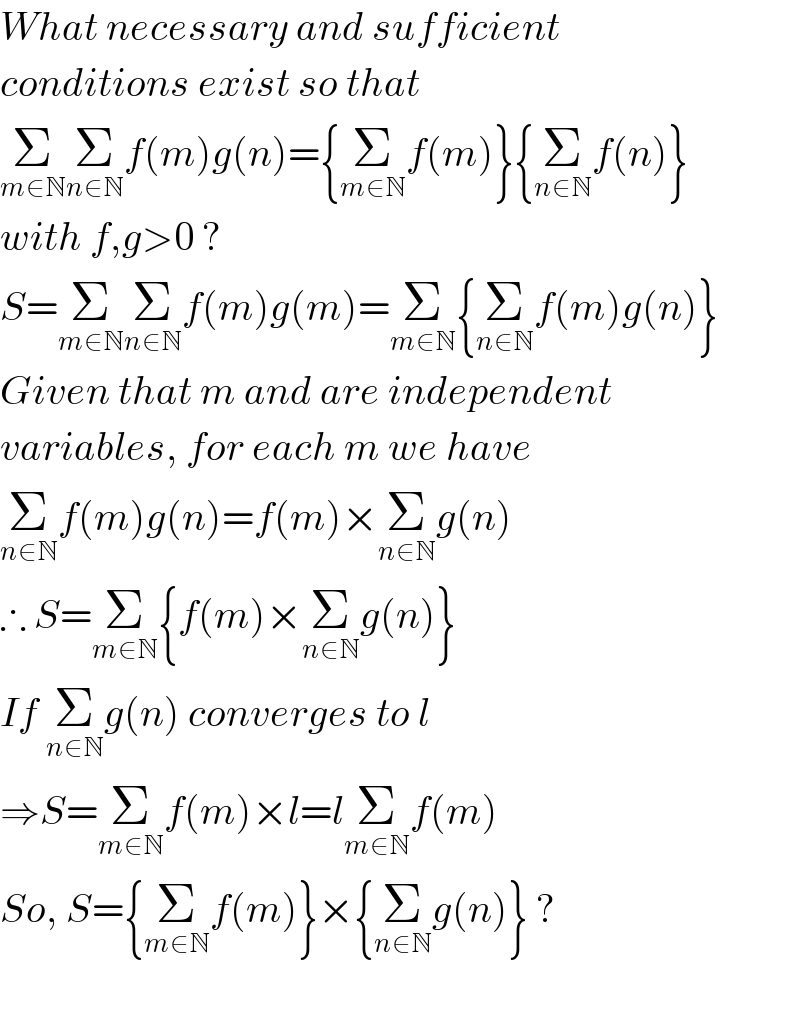
What necessary and sufficient conditions exist so that Σ_(m∈N) Σ_(n∈N) f(m)g(n)={Σ_(m∈N) f(m)}{Σ_(n∈N) f(n)} with f,g>0 ? S=Σ_(m∈N) Σ_(n∈N) f(m)g(m)=Σ_(m∈N) {Σ_(n∈N) f(m)g(n)} Given that m and are independent variables, for each m we have Σ_(n∈N) f(m)g(n)=f(m)×Σ_(n∈N) g(n) ∴ S=Σ_(m∈N) {f(m)×Σ_(n∈N) g(n)} If Σ_(n∈N) g(n) converges to l ⇒S=Σ_(m∈N) f(m)×l=lΣ_(m∈N) f(m) So, S={Σ_(m∈N) f(m)}×{Σ_(n∈N) g(n)} ?

$${What}\:{necessary}\:{and}\:{sufficient}\: \\ $$$${conditions}\:{exist}\:{so}\:{that} \\ $$$$\underset{{m}\in\mathbb{N}} {\sum}\underset{{n}\in\mathbb{N}} {\sum}{f}\left({m}\right){g}\left({n}\right)=\left\{\underset{{m}\in\mathbb{N}} {\sum}{f}\left({m}\right)\right\}\left\{\underset{{n}\in\mathbb{N}} {\sum}{f}\left({n}\right)\right\}\: \\ $$$${with}\:{f},{g}>\mathrm{0}\:? \\ $$$${S}=\underset{{m}\in\mathbb{N}} {\sum}\underset{{n}\in\mathbb{N}} {\sum}{f}\left({m}\right){g}\left({m}\right)=\underset{{m}\in\mathbb{N}} {\sum}\left\{\underset{{n}\in\mathbb{N}} {\sum}{f}\left({m}\right){g}\left({n}\right)\right\} \\ $$$${Given}\:{that}\:{m}\:{and}\:{are}\:{independent} \\ $$$${variables},\:{for}\:{each}\:{m}\:{we}\:{have}\: \\ $$$$\underset{{n}\in\mathbb{N}} {\sum}{f}\left({m}\right){g}\left({n}\right)={f}\left({m}\right)×\underset{{n}\in\mathbb{N}} {\sum}{g}\left({n}\right) \\ $$$$\therefore\:{S}=\underset{{m}\in\mathbb{N}} {\sum}\left\{{f}\left({m}\right)×\underset{{n}\in\mathbb{N}} {\sum}{g}\left({n}\right)\right\} \\ $$$${If}\:\underset{{n}\in\mathbb{N}} {\sum}{g}\left({n}\right)\:{converges}\:{to}\:{l} \\ $$$$\Rightarrow{S}=\underset{{m}\in\mathbb{N}} {\sum}{f}\left({m}\right)×{l}={l}\underset{{m}\in\mathbb{N}} {\sum}{f}\left({m}\right) \\ $$$${So},\:{S}=\left\{\underset{{m}\in\mathbb{N}} {\sum}{f}\left({m}\right)\right\}×\left\{\underset{{n}\in\mathbb{N}} {\sum}{g}\left({n}\right)\right\}\:? \\ $$$$ \\ $$

Commented by prakash jain last updated on 19/Dec/15

f(m) is constant for summation over n. taking a constant out for summation is always valid (even if the series is divergent). absolute convergence is required for rearrangmnt changing order of summation.

$${f}\left({m}\right)\:{is}\:{constant}\:{for}\:{summation}\:{over}\:{n}. \\ $$$${taking}\:{a}\:{constant}\:{out}\:{for}\:{summation}\:{is} \\ $$$${always}\:{valid}\:\left({even}\:{if}\:{the}\:{series}\:{is}\:{divergent}\right). \\ $$$${absolute}\:{convergence}\:{is}\:{required}\:{for}\:{rearrangmnt} \\ $$$${changing}\:{order}\:{of}\:{summation}. \\ $$

Commented by Yozzii last updated on 19/Dec/15

Thank you.

$${Thank}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com