
Question Number 37359 by math khazana by abdo last updated on 12/Jun/18
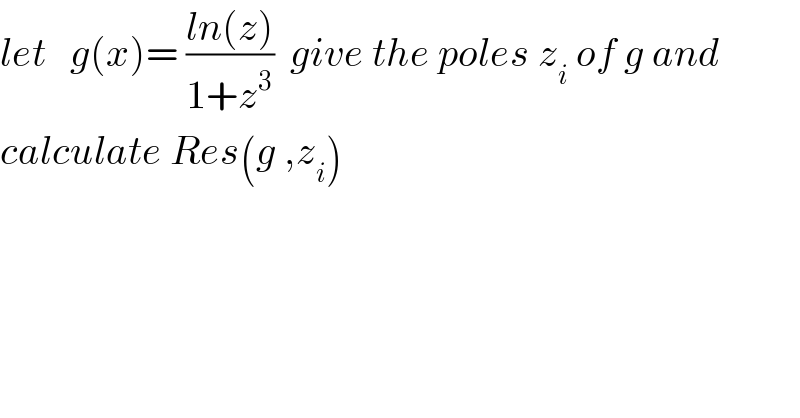
$${let}\:\:\:{g}\left({x}\right)=\:\frac{{ln}\left({z}\right)}{\mathrm{1}+{z}^{\mathrm{3}} }\:\:{give}\:{the}\:{poles}\:{z}_{{i}} \:{of}\:{g}\:{and} \\ $$$${calculate}\:{Res}\left({g}\:,{z}_{{i}} \right)\: \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 13/Jun/18
![poles of g 1+z^3 =0 ⇔z^3 =e^(iπ) so if z=re^(iθ) ⇒r=1 and 3θ =(2k+1)π ⇒θ=(2k+1)(π/3) the roots are z_k =e^(i(2k+1)(π/3)) with k∈[[0,2]] z_0 =e^(i(π/3)) , z_1 =−1 , z_2 = e^(i((4π)/3)) g(z) = ((ln(z))/((z−z_0 )(z−z_1 )(z−z_2 )))= ((lnz)/((z+1)(z^2 −z+1))) Res(g,z_1 ) = ((ln(z_1 ))/(z_1 ^2 −z_1 +1)) = iπ (1/3) =i(π/3) Res(g,z_0 ) = ((ln(z_0 ))/((z_0 −z_1 )(z_0 −z_2 ))) =i(π/3) (1/((e^(i(π/3)) +1)(e^(i(π/3)) −e^(i((4π)/3)) ))) =i(π/3) (1/(((3/2) +i((√3)/2))((3/2)+i((√3)/2) +(1/2) +i((√3)/2)))) =i(π/3) (1/(((3/2) +i((√3)/2))(2 +i(√3)))) = ((2iπ)/(3(3+i(√3))(2+i(√3)))) Res(g,z_2 ) = ((ln(z_2 ))/((z_2 −z_0 )(z_2 −z_1 ))) =i((4π)/3) (1/((e^(i4(π/3)) −e^(i(π/3)) )(e^(i((4π)/3)) +1)))](Q37477.png)
$${poles}\:{of}\:{g}\:\:\:\mathrm{1}+{z}^{\mathrm{3}} =\mathrm{0}\:\Leftrightarrow{z}^{\mathrm{3}} \:={e}^{{i}\pi} \:\:{so}\:{if}\:{z}={re}^{{i}\theta} \\ $$$$\Rightarrow{r}=\mathrm{1}\:{and}\:\mathrm{3}\theta\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{3}} \\ $$$${the}\:{roots}\:{are}\:{z}_{{k}} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{3}}} \:\:{with}\:{k}\in\left[\left[\mathrm{0},\mathrm{2}\right]\right] \\ $$$${z}_{\mathrm{0}} ={e}^{{i}\frac{\pi}{\mathrm{3}}} \:\:\:\:,\:{z}_{\mathrm{1}} =−\mathrm{1}\:\:\:\:,\:\:{z}_{\mathrm{2}} =\:{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \:\:\:\:\:\: \\ $$$${g}\left({z}\right)\:=\:\frac{{ln}\left({z}\right)}{\left({z}−{z}_{\mathrm{0}} \right)\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}=\:\frac{{lnz}}{\left({z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} −{z}+\mathrm{1}\right)} \\ $$$${Res}\left({g},{z}_{\mathrm{1}} \right)\:=\:\:\frac{{ln}\left({z}_{\mathrm{1}} \right)}{{z}_{\mathrm{1}} ^{\mathrm{2}} \:−{z}_{\mathrm{1}} +\mathrm{1}}\:=\:{i}\pi\:\frac{\mathrm{1}}{\mathrm{3}}\:={i}\frac{\pi}{\mathrm{3}} \\ $$$${Res}\left({g},{z}_{\mathrm{0}} \right)\:=\:\frac{{ln}\left({z}_{\mathrm{0}} \right)}{\left({z}_{\mathrm{0}} −{z}_{\mathrm{1}} \right)\left({z}_{\mathrm{0}} −{z}_{\mathrm{2}} \right)}\:={i}\frac{\pi}{\mathrm{3}}\:\frac{\mathrm{1}}{\left({e}^{{i}\frac{\pi}{\mathrm{3}}} \:+\mathrm{1}\right)\left({e}^{{i}\frac{\pi}{\mathrm{3}}} \:−{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \right)} \\ $$$$={i}\frac{\pi}{\mathrm{3}}\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\mathrm{3}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \\ $$$$={i}\frac{\pi}{\mathrm{3}}\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\mathrm{2}\:+{i}\sqrt{\mathrm{3}}\right)}\:=\:\frac{\mathrm{2}{i}\pi}{\mathrm{3}\left(\mathrm{3}+{i}\sqrt{\mathrm{3}}\right)\left(\mathrm{2}+{i}\sqrt{\mathrm{3}}\right)} \\ $$$${Res}\left({g},{z}_{\mathrm{2}} \right)\:=\:\frac{{ln}\left({z}_{\mathrm{2}} \right)}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{0}} \right)\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)} \\ $$$$={i}\frac{\mathrm{4}\pi}{\mathrm{3}}\:\frac{\mathrm{1}}{\left({e}^{{i}\mathrm{4}\frac{\pi}{\mathrm{3}}} \:−{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\left({e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \:+\mathrm{1}\right)} \\ $$
