
Question and Answers Forum
Question Number 37540 by rahul 19 last updated on 14/Jun/18
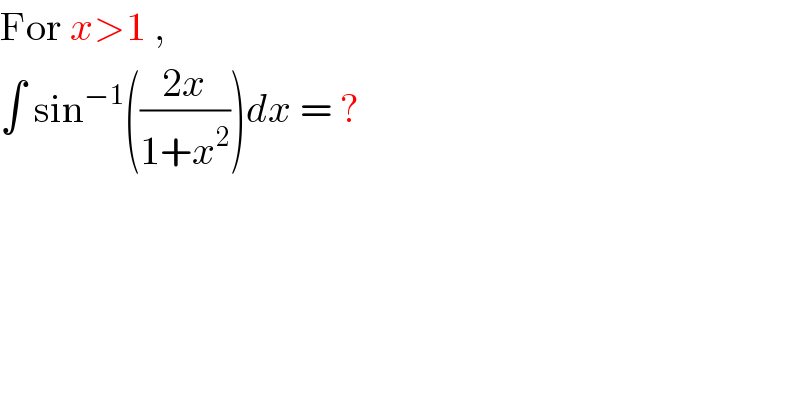
Answered by ajfour last updated on 14/Jun/18
![let x=tan θ x>1 ⇒ nπ+(π/4) < θ < nπ+(π/2) ⇒ ((2x)/(1+x^2 )) = sin 2θ 2nπ+(π/2) < 2θ < 2nπ+π sin^(−1) (sin 2θ) = sin^(−1) sin (π−2θ) 2mπ < π−2θ < 2mπ+(π/2) m=0 is appropriate since π−2θ should lie in [−(π/2), (π/2)] sin^(−1) sin (π−2θ)= π−2θ = π−2tan^(−1) x I=∫(π−2tan^(−1) x)dx =πx−2(xtan^(−1) x−(1/2)∫ ((2xdx)/(1+x^2 )) )+c I=πx−2xtan^(−1) x+ln ∣1+x^2 ∣+c .](Q37543.png)
Commented byrahul 19 last updated on 14/Jun/18
thank you sir. ����
Commented byrahul 19 last updated on 14/Jun/18
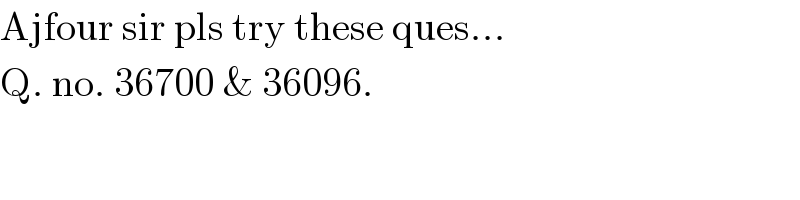
| ||
Question and Answers Forum | ||
Question Number 37540 by rahul 19 last updated on 14/Jun/18 | ||
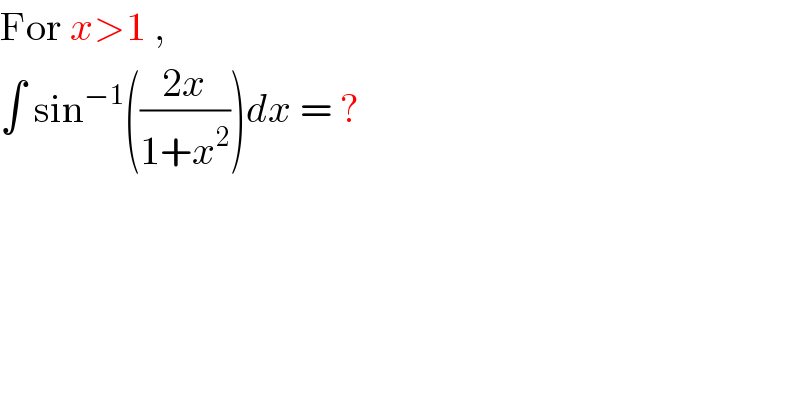 | ||
Answered by ajfour last updated on 14/Jun/18 | ||
![let x=tan θ x>1 ⇒ nπ+(π/4) < θ < nπ+(π/2) ⇒ ((2x)/(1+x^2 )) = sin 2θ 2nπ+(π/2) < 2θ < 2nπ+π sin^(−1) (sin 2θ) = sin^(−1) sin (π−2θ) 2mπ < π−2θ < 2mπ+(π/2) m=0 is appropriate since π−2θ should lie in [−(π/2), (π/2)] sin^(−1) sin (π−2θ)= π−2θ = π−2tan^(−1) x I=∫(π−2tan^(−1) x)dx =πx−2(xtan^(−1) x−(1/2)∫ ((2xdx)/(1+x^2 )) )+c I=πx−2xtan^(−1) x+ln ∣1+x^2 ∣+c .](Q37543.png) | ||
| ||
Commented byrahul 19 last updated on 14/Jun/18 | ||
thank you sir. ���� | ||
Commented byrahul 19 last updated on 14/Jun/18 | ||
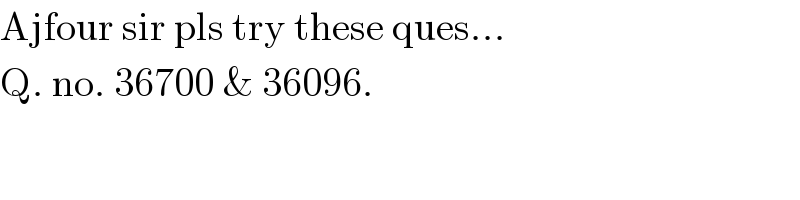 | ||