
Question and Answers Forum
Question Number 37582 by behi83417@gmail.com last updated on 15/Jun/18

Commented by ajfour last updated on 15/Jun/18

Commented by behi83417@gmail.com last updated on 15/Jun/18
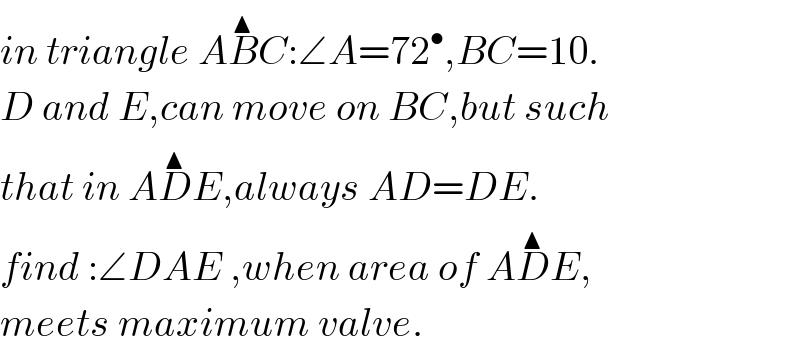
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jun/18
Answered by ajfour last updated on 16/Jun/18
![let ∠DAE=θ ; ∠ACB=φ in △ABC (a/(sin α))=(b/(sin (α+φ))) ....(i) in △ ACE (b/(sin θ))=((2ρcos θ)/(sin φ)) ....(ii) S_(ADE) =S =(ρ/2)(bsin φ) ....(iii) using (ii) in (iii( S =((b^2 sin^2 φ)/(2sin 2θ)) using (i) S(θ,φ)=(((a^2 sin^2 (α+φ))/(sin^2 α)))(((sin^2 φ)/(2sin 2θ))) When S is maximum (∂S/∂θ) =0 ; ⇒ (∂S/∂θ)= ((a^2 sin^2 (α+φ)sin^2 φ)/(2sin^2 α))(− ((2cos 2θ)/(sin^2 2θ)))=0 ⇒ cos 2θ=0 or 𝛉=(𝛑/4) . (∂S/∂φ)=(a^2 /(2sin^2 αsin 2θ))[sin 2φsin^2 (α+φ) +sin^2 φsin (2α+2φ)]=0 ⇒ cos φ[1−cos (2α+2φ)] = − sin φsin (2α+2φ) or cos φ= cos (2α+3φ) ⇒ 2π−φ = 2α+3φ 𝛗 = (𝛑/2)−(𝛂/2) S_(max) =((a^2 sin^2 ((π/2)+(α/2))sin^2 ((π/2)−(α/2)))/(2sin^2 α)) =(a^2 /4)tan^2 ((α/2)) . E lies on BC produced towards right. ∠ADE = (π/2) (yes) ∠DAE = (π/4) to meet such a condition.](Q37612.png)
Commented by behi83417@gmail.com last updated on 16/Jun/18
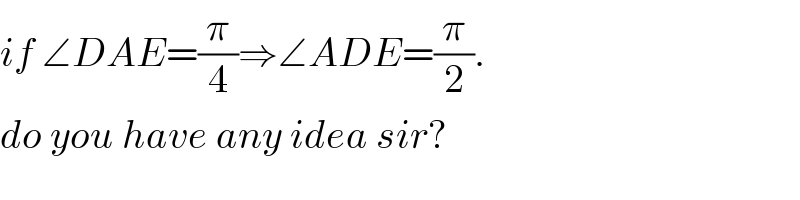
Commented by behi83417@gmail.com last updated on 15/Jun/18

Commented by ajfour last updated on 15/Jun/18
Commented by behi83417@gmail.com last updated on 15/Jun/18

