find the value of f(a)= ∫_0 ^∞ ((x^2 −1)/((x^4 +a^4 )^2 ))dx 2) calculate ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 37602 by prof Abdo imad last updated on 15/Jun/18

$f i n d t h e v a l u e o f$ $f (a) = \int_{0}^{\infty} \frac{x^{2} - 1}{{(x^{4} + a^{4})}^{2}} d x$ $2) c a l c u l a t e \int_{0}^{\infty} \frac{x^{2} - 1}{{(x^{4} + 1)}^{2}} d x$
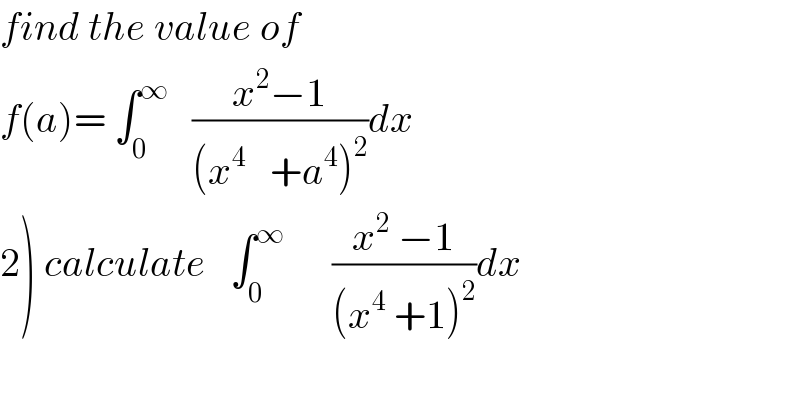
Commented by prof Abdo imad last updated on 16/Jun/18
$1) we have f(a)=∫_(−∞) ^(+∞) ((x^2 −1)/((x^4 +a^4 )^2 ))dx let ϕ(z)= ((z^2 −1)/((z^4 +a^4 )^2 )) ϕ(z)= ((z^2 −1)/({ (z^2 )^2 −(ia^2 )^2 }^2 )) =((z^2 −1)/((z^2 −ia^2 )^2 (z^2 +ia^2 )^2 )) =((z^2 −1)/((z −a e^(i(π/4)) )^2 ( z+ae^((iπ)/4) )^2 (z−a e^(−((iπ)/4)) )^2 (z+a e^(−((iπ)/4)) )^2 )) the poles of ϕ are +^− e^(i(π/4)) and +^− e^(−((iπ)/4)) (doubles) let suppose a>0 ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ, ae^((iπ)/4) ) +Res(ϕ,−ae^(−((iπ)/4)) )} Res(ϕ,ae^(i(π/4)) ) =lim_(z→ae^((iπ)/4) ) (1/((2−1)!)){(z−ae^((iπ)/4) )^2 ϕ(z)}^((1)) =lim_(z→ ae^((iπ)/4) ) { ((z^2 −1)/((z+a e^((iπ)/4) )^2 (z^2 +ia^2 )^2 ))}^((1)) =lim_(z→ ae^((iπ)/4) ) ((2z(z+ae^((iπ)/4) )(z^2 +ia^2 )^2 −(z^2 −1)(2(z+ae^((iπ)/4) )(z^2 +ia^2 )^2 +4z(z^2 +ia^2 )(z+ae^((iπ)/4) )^2 )/((z +ae^((iπ)/4) )^4 ( z^2 +ia^2 )^4 )) =lim_(z→a e^((iπ)/4) ) ((2z(z^2 +ia^2 )−(z^2 −1){ 2(z^2 +ia^2 )+4z(z+ae^((iπ)/4) )})/((z +a e^((iπ)/4) )^3 (z^2 +ia^2 )^3 )) =((2a e^((iπ)/4) (2ia^2 ) −(ia^2 −1){4ia^2 +4ae^((iπ)/4) (2ae^((iπ)/4) )})/((2ae^(i(π/4)) )^3 (2ia^2 )^3 )) =((4ia^3 e^((iπ)/4) −(ia^2 −1){ 4ia^2 +8a^2 i))/(8a^3 i e^((iπ)/4) (−8ia^6 ))) =(( 4ia^3 e^((iπ)/4) −12ia^2 (ia^2 −1))/(64 a^9 e^((iπ)/4) )) =((4ia^(3 ) e^((iπ)/4) +12a^4 +12ia^2 )/(64a^9 e^((iπ)/4) )) =.....$
$1) w e h a v e f (a) = \int_{- \infty}^{+ \infty} \frac{x^{2} - 1}{{(x^{4} + a^{4})}^{2}} d x$ $l e t φ (z) = \frac{z^{2} - 1}{{(z^{4} + a^{4})}^{2}}$ $φ (z) = \frac{z^{2} - 1}{{{(z^{2})}^{2} - {({i a}^{2})}^{2}}^{2}}$ $= \frac{z^{2} - 1}{{(z^{2} - {i a}^{2})}^{2} {(z^{2} + {i a}^{2})}^{2}}$ $= \frac{z^{2} - 1}{{(z - a e^{i \frac{π}{4}})}^{2} {(z + {a e}^{\frac{i π}{4}})}^{2} {(z - a e^{- \frac{i π}{4}})}^{2} {(z + a e^{- \frac{i π}{4}})}^{2}}$ $t h e p o l e s o f φ a r e \bar{+} e^{i \frac{π}{4}} a n d \bar{+} e^{- \frac{i π}{4}} (d o u b l e s)$ $l e t s u p p o s e a > 0$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π {R e s (φ, {a e}^{\frac{i π}{4}}) + R e s (φ, - {a e}^{- \frac{i π}{4}})}$ $R e s (φ, {a e}^{i \frac{π}{4}}) = {l i m}_{z \to {a e}^{\frac{i π}{4}}} \frac{1}{(2 - 1)!} {{(z - {a e}^{\frac{i π}{4}})}^{2} φ (z)}^{(1)}$ $= {l i m}_{z \to {a e}^{\frac{i π}{4}}} {\frac{z^{2} - 1}{{(z + a e^{\frac{i π}{4}})}^{2} {(z^{2} + {i a}^{2})}^{2}}}^{(1)}$ $= {l i m}_{z \to {a e}^{\frac{i π}{4}}} \frac{2 z (z + {a e}^{\frac{i π}{4}}) {(z^{2} + {i a}^{2})}^{2} - (z^{2} - 1) (2 (z + {a e}^{\frac{i π}{4}}) {(z^{2} + {i a}^{2})}^{2} + 4 z (z^{2} + {ia}^{2}) {(z + {ae}^{\frac{i π}{4}})}^{2}}{{(z + {a e}^{\frac{i π}{4}})}^{4} {(z^{2} + {i a}^{2})}^{4}}$ $= {l i m}_{z \to a e^{\frac{i π}{4}}} \frac{2 z (z^{2} + {i a}^{2}) - (z^{2} - 1) {2 (z^{2} + {i a}^{2}) + 4 z (z + {a e}^{\frac{i π}{4}})}}{{(z + a e^{\frac{i π}{4}})}^{3} {(z^{2} + {i a}^{2})}^{3}}$ $= \frac{2 a e^{\frac{i π}{4}} (2 {i a}^{2}) - ({i a}^{2} - 1) {4 {i a}^{2} + 4 {a e}^{\frac{i π}{4}} (2 {a e}^{\frac{i π}{4}})}}{{(2 {a e}^{i \frac{π}{4}})}^{3} {(2 {i a}^{2})}^{3}}$ $= \frac{4 {i a}^{3} e^{\frac{i π}{4}} - ({i a}^{2} - 1) {4 {i a}^{2} + 8 a^{2} i)}{8 a^{3} i e^{\frac{i π}{4}} (- 8 {i a}^{6})}$ $= \frac{4 {i a}^{3} e^{\frac{i π}{4}} - 12 {i a}^{2} ({i a}^{2} - 1)}{64 a^{9} e^{\frac{i π}{4}}}$ $= \frac{4 {i a}^{3} e^{\frac{i π}{4}} + 12 a^{4} + 12 {i a}^{2}}{64 a^{9} e^{\frac{i π}{4}}} = . . . . .$
Commented by behi83417@gmail.com last updated on 16/Jun/18

$x = a \sqrt{t g t} \Rightarrow d x = \frac{a (1 + {t g}^{2} t) d t}{2 \sqrt{t g t}}$ $I = \int \frac{a^{2} t g t - 1}{{(a^{4} {t g}^{2} t + a^{4})}^{2}} . \frac{a (1 + {t g}^{2} t) d t}{2 \sqrt{t g t}}$ $\Rightarrow I = \int \frac{a^{2} t g t - 1}{a^{8} {({t g}^{2} t + 1)}^{2}} . \frac{a (1 + {t g}^{2} t) d t}{2 \sqrt{t g t}} =$ $= \frac{1}{a^{7}} \int \frac{a^{2} t g t - 1}{2 \sqrt{t g t} (1 + {t g}^{2} t)} d t, t g t = u^{2}$ $(1 + {t g}^{2} t) d t = 2 u d u \Rightarrow d t = \frac{2 u d u}{1 + u^{4}}$ $\Rightarrow I = \frac{1}{a^{7}} \int \frac{a^{2} u^{2} - 1}{2 u (1 + u^{4})} . \frac{2 u d u}{1 + u^{4}} = \frac{1}{a^{7}} \int \frac{a^{2} u^{2} - 1}{{(1 + u^{4})}^{2}} d u =$ $= \frac{1}{a^{7}} [\int \frac{a^{2} u^{2}}{{(1 + u^{4})}^{2}} d u - \int \frac{d u}{{(1 + u^{4})}^{2}}] = . . .$ $You can't use 'macro parameter character #' in math mode$ $+ \frac{\sqrt{2}}{16} l n \frac{u^{2} - u \sqrt{2} + 1}{\sqrt{1 + u^{4}}} + c o n s t$ $You can't use 'macro parameter character #' in math mode$ $- \frac{3 \sqrt{2}}{16} l n \frac{u^{2} - u \sqrt{2} + 1}{\sqrt{1 + u^{4}}} + c o n s t$ $b y s y m p l i f i n g :$ $You can't use 'macro parameter character #' in math mode$ $c h a n g e \Rightarrow u \to \frac{x}{a}$ $I = \frac{1}{a^{5}} [\frac{{a x}^{3}}{4 (a^{4} + x^{4})} + \frac{\sqrt{2}}{16} {t g}^{- 1} (\frac{a x \sqrt{2}}{a^{2} - x^{2}}) -$ $- \frac{3 \sqrt{2}}{16} l n \frac{x^{2} - a x \sqrt{2} + a^{2}}{\sqrt{a^{4} + x^{4}}}] - \frac{1}{a^{7}} [\frac{a^{3} x}{4 (a^{4} + x^{4})} +$ $+ \frac{3 \sqrt{2}}{16} {t g}^{- 1} \frac{a x \sqrt{2}}{a^{2} - x^{2}} - \frac{3 \sqrt{2}}{16} l n \frac{x^{2} - a x \sqrt{2} + a^{2}}{\sqrt{a^{4} + x^{4}}}] + c o n s t$ $3) I = F (\infty) - F (0) = 0$ $4) a = 1 \Rightarrow I = \frac{1}{8} [\frac{2 x}{1 + x^{4}} + 2 \sqrt{2} {t g}^{- 1} \frac{x \sqrt{2}}{1 - x^{2}} -$ $- \sqrt{2} l n \frac{x^{2} - x \sqrt{2} + 1}{\sqrt{1 + x^{4}}}] + c o n s t . ◼$
Commented by behi83417@gmail.com last updated on 16/Jun/18

$d e a r p r o f . a b d o! i s i t o k ?$
Commented by prof Abdo imad last updated on 16/Jun/18

$s i r B e h i y o u h a v e u s i n g a g o o d c h a n g e m e n t$ $a t t h e b e g i n i n g a n d i t s s e e m s t h a t y o u r m e t h o d$ $i s c o r r e c t a n d i w i l l g i v e y o u t h e f i n a l a n s w e r$ $a f t e r f i n i s h i n g t h e c a l c u l u s . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum