Question and Answers Forum
Question Number 37627 by Joel579 last updated on 16/Jun/18
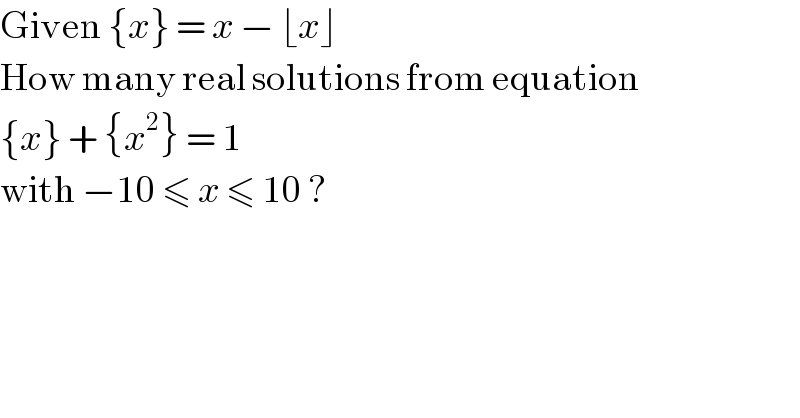
Answered by ajfour last updated on 16/Jun/18
![let x=m+h where m∈Z and h={x} {x}+{x^2 }=1 ⇒ h+(m+h)^2 −[(m+h)^2 ]=1 h+m^2 +2mh+h^2 −m^2 −[2mh+h^2 ]=1 ⇒ {2mh+h^2 }=1−h ⇒ h≠ 0 ...](Q37641.png)
Commented by Rasheed.Sindhi last updated on 17/Jun/18

Answered by ajfour last updated on 16/Jun/18
Answered by MJS last updated on 16/Jun/18
![for x>0 we must solve equations x∈[0;1[ (x−0)+(x^2 −0)=1 ⇒ x^2 +x−1=0 x∈[1;2[ (x−1)+(x^2 −1)=1 ⇒ x^2 +x−3=0 (x−1)+(x^2 −2)=1 ⇒ x^2 +x−4=0 (x−1)+(x^2 −3)=1 ⇒ x^2 +x−5=0 x∈[2;3[ (x−2)+(x^2 −4)=1 ⇒ x^2 +x−7=0 ... (x−2)+(x^2 −8)=1 ⇒ x^2 +x−11=0 x∈[n;n+1] (x−n)+(x^2 −n^2 )=1 ⇒ x^2 +x−(n^2 +n+1)=0 ... (x−n)+(x^2 −((n+1)^2 −1))=1 ⇒ ⇒ x^2 +x−(n^2 +3n+1)=0 we have 1+3+5+7+9+11+13+15+17+19= = 100 solutions in [0;10] for x<0 the negative solutions of above equations count ⇒ we have no solution in [−1;0[ 1 solution in [−2;−1[ 3 solutions in [−3;−2[ ... so we have 100+100−19=181 solutions in [−10;10]](Q37697.png)
Commented by Rasheed.Sindhi last updated on 17/Jun/18