Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3775 by Yozzii last updated on 20/Dec/15

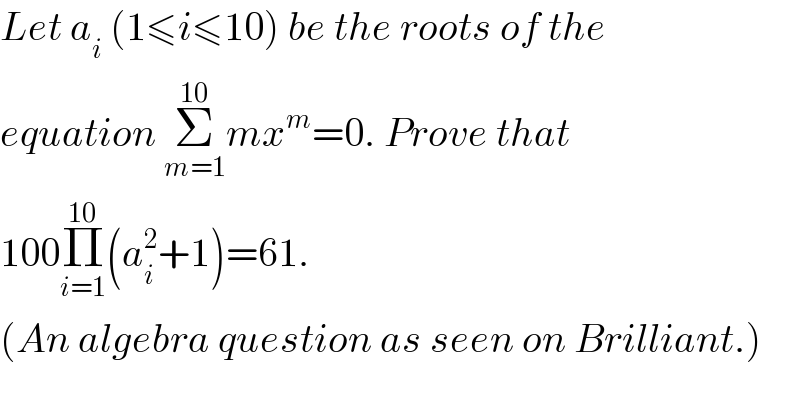
Let a_i (1≤i≤10) be the roots of the equation Σ_(m=1) ^(10) mx^m =0. Prove that 100Π_(i=1) ^(10) (a_i ^2 +1)=61. (An algebra question as seen on Brilliant.)

$${Let}\:{a}_{{i}} \:\left(\mathrm{1}\leqslant{i}\leqslant\mathrm{10}\right)\:{be}\:{the}\:{roots}\:{of}\:{the} \\ $$$${equation}\:\underset{{m}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{mx}^{{m}} =\mathrm{0}.\:{Prove}\:{that} \\ $$$$\mathrm{100}\underset{{i}=\mathrm{1}} {\overset{\mathrm{10}} {\prod}}\left({a}_{{i}} ^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{61}. \\ $$$$\left({An}\:{algebra}\:{question}\:{as}\:{seen}\:{on}\:{Brilliant}.\right) \\ $$

Commented by prakash jain last updated on 20/Dec/15

LHS=S=x+2x^2 +3x^3 +...+10x^(10) xS= x^2 +2x^3 +...+9x^(10) +10x^(11) (1−x)S=x+x^2 +...+x^(10) −10x^(11) x(1−x)S= x^2 +.....+x^(10) +x^(11) −10x^(12) (1−x)S=((x(x^(10) −1))/(x−1))−10x^(11) S=((x^(11) −x−10x^(12) +10x^(11) )/((x−1)(1−x))) S=((10x^(12) −11x^(11) +x)/((1−x)^2 )) 10x^(12) −11x^(11) +x=0 This equation will give 12 solution (2 are equal 1) remain 10 are solution of the original equation.

$$\mathrm{LHS}={S}={x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +...+\mathrm{10}{x}^{\mathrm{10}} \\ $$$${xS}=\:\:\:{x}^{\mathrm{2}} \:\:\:\:\:+\mathrm{2}{x}^{\mathrm{3}} +...+\mathrm{9}{x}^{\mathrm{10}} +\mathrm{10}{x}^{\mathrm{11}} \\ $$$$\left(\mathrm{1}−{x}\right){S}={x}+{x}^{\mathrm{2}} +...+{x}^{\mathrm{10}} −\mathrm{10}{x}^{\mathrm{11}} \\ $$$${x}\left(\mathrm{1}−{x}\right){S}=\:\:{x}^{\mathrm{2}} +.....+{x}^{\mathrm{10}} +{x}^{\mathrm{11}} −\mathrm{10}{x}^{\mathrm{12}} \\ $$$$\left(\mathrm{1}−{x}\right){S}=\frac{{x}\left({x}^{\mathrm{10}} −\mathrm{1}\right)}{{x}−\mathrm{1}}−\mathrm{10}{x}^{\mathrm{11}} \\ $$$${S}=\frac{{x}^{\mathrm{11}} −{x}−\mathrm{10}{x}^{\mathrm{12}} +\mathrm{10}{x}^{\mathrm{11}} }{\left({x}−\mathrm{1}\right)\left(\mathrm{1}−{x}\right)} \\ $$$${S}=\frac{\mathrm{10}{x}^{\mathrm{12}} −\mathrm{11}{x}^{\mathrm{11}} +{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{10}{x}^{\mathrm{12}} −\mathrm{11}{x}^{\mathrm{11}} +{x}=\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{will}\:\mathrm{give}\:\mathrm{12}\:\mathrm{solution}\:\left(\mathrm{2}\:\mathrm{are}\right. \\ $$$$\left.\mathrm{equal}\:\mathrm{1}\right)\:\mathrm{remain}\:\mathrm{10}\:\mathrm{are}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{original} \\ $$$$\mathrm{equation}. \\ $$

Commented by Yozzii last updated on 20/Dec/15

Yes.

$${Yes}.\: \\ $$

Commented by Yozzii last updated on 20/Dec/15

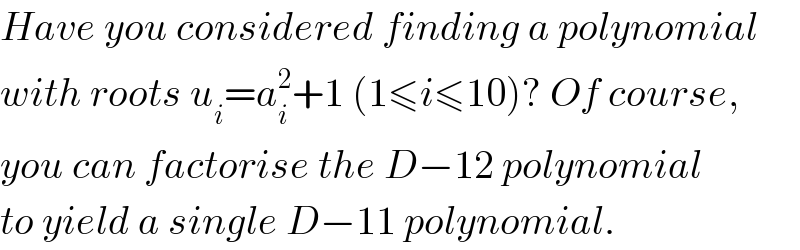
Have you considered finding a polynomial with roots u_i =a_i ^2 +1 (1≤i≤10)? Of course, you can factorise the D−12 polynomial to yield a single D−11 polynomial.

$${Have}\:{you}\:{considered}\:{finding}\:{a}\:{polynomial} \\ $$$${with}\:{roots}\:{u}_{{i}} ={a}_{{i}} ^{\mathrm{2}} +\mathrm{1}\:\left(\mathrm{1}\leqslant{i}\leqslant\mathrm{10}\right)?\:{Of}\:{course}, \\ $$$${you}\:{can}\:{factorise}\:{the}\:{D}−\mathrm{12}\:{polynomial} \\ $$$${to}\:{yield}\:{a}\:{single}\:{D}−\mathrm{11}\:{polynomial}. \\ $$

Commented by Yozzii last updated on 20/Dec/15

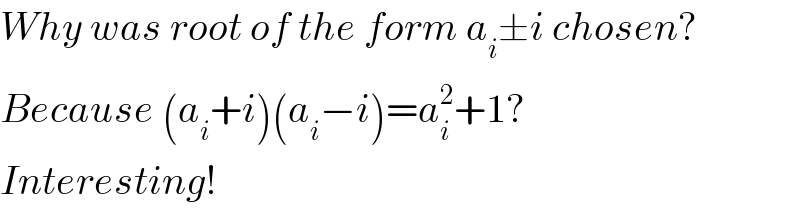
Why was root of the form a_i ±i chosen? Because (a_i +i)(a_i −i)=a_i ^2 +1? Interesting!

$${Why}\:{was}\:{root}\:{of}\:{the}\:{form}\:{a}_{{i}} \pm{i}\:{chosen}? \\ $$$${Because}\:\left({a}_{{i}} +{i}\right)\left({a}_{{i}} −{i}\right)={a}_{{i}} ^{\mathrm{2}} +\mathrm{1}?\: \\ $$$${Interesting}! \\ $$

Commented by prakash jain last updated on 20/Dec/15

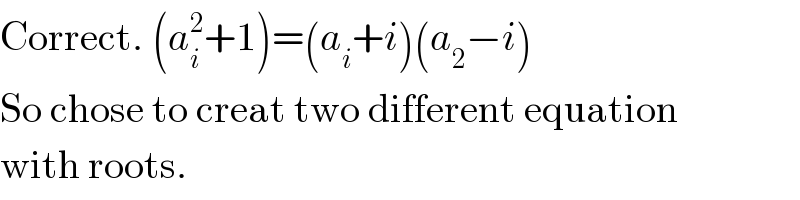
Correct. (a_i ^2 +1)=(a_i +i)(a_2 −i) So chose to creat two different equation with roots.

$$\mathrm{Correct}.\:\left({a}_{{i}} ^{\mathrm{2}} +\mathrm{1}\right)=\left({a}_{{i}} +{i}\right)\left({a}_{\mathrm{2}} −{i}\right) \\ $$$$\mathrm{So}\:\mathrm{chose}\:\mathrm{to}\:\mathrm{creat}\:\mathrm{two}\:\mathrm{different}\:\mathrm{equation} \\ $$$$\mathrm{with}\:\mathrm{roots}. \\ $$

Commented by prakash jain last updated on 20/Dec/15

Thanks.Trying equation with root a_i +i and a_i −i 10x^(12) −11x^(11) +x=0 10(x+i)^(12) −11(x+i)^(11) +(x+i)=0 ...(A) product of roots=((10i^(12) −11i^(11) +i)/(10))=((10+12i)/(10)) 10(x−i)^(12) −11(x−i)^(11) +(x−i)=0 ...(B) product of roots=((10i^(12) +11i^(11) −i)/(10))=((10−12i)/(10)) Π_(i=1) ^(10) (a_i ^2 +1)=((product of root of A×product of root of B)/((1+i)^2 (1−i)^2 [divide by extra roots from(x−1)^2 ])) =((10−12i)/(10))×((10+12i)/(10))×(1/2^2 )=((244)/(100×4))=((61)/(100))

$$\mathrm{Thanks}.\mathrm{Trying}\:\mathrm{equation}\:\mathrm{with}\:\mathrm{root}\:{a}_{{i}} +{i}\:{and}\:{a}_{{i}} −{i} \\ $$$$\mathrm{10}{x}^{\mathrm{12}} −\mathrm{11}{x}^{\mathrm{11}} +{x}=\mathrm{0} \\ $$$$\mathrm{10}\left({x}+{i}\right)^{\mathrm{12}} −\mathrm{11}\left({x}+{i}\right)^{\mathrm{11}} +\left({x}+{i}\right)=\mathrm{0}\:\:\:...\left({A}\right) \\ $$$${product}\:{of}\:{roots}=\frac{\mathrm{10}{i}^{\mathrm{12}} −\mathrm{11}{i}^{\mathrm{11}} +{i}}{\mathrm{10}}=\frac{\mathrm{10}+\mathrm{12}{i}}{\mathrm{10}} \\ $$$$\mathrm{10}\left({x}−{i}\right)^{\mathrm{12}} −\mathrm{11}\left({x}−{i}\right)^{\mathrm{11}} +\left({x}−{i}\right)=\mathrm{0}\:\:\:...\left(\mathrm{B}\right) \\ $$$${product}\:{of}\:{roots}=\frac{\mathrm{10}{i}^{\mathrm{12}} +\mathrm{11}{i}^{\mathrm{11}} −{i}}{\mathrm{10}}=\frac{\mathrm{10}−\mathrm{12}{i}}{\mathrm{10}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{10}} {\prod}}\left({a}_{{i}} ^{\mathrm{2}} +\mathrm{1}\right)=\frac{\mathrm{product}\:\mathrm{of}\:\mathrm{root}\:\mathrm{of}\:\mathrm{A}×\mathrm{product}\:\mathrm{of}\:\mathrm{root}\:\mathrm{of}\:\mathrm{B}}{\left(\mathrm{1}+{i}\right)^{\mathrm{2}} \left(\mathrm{1}−{i}\right)^{\mathrm{2}} \:\left[{divide}\:{by}\:{extra}\:{roots}\:{from}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right]} \\ $$$$=\frac{\mathrm{10}−\mathrm{12}{i}}{\mathrm{10}}×\frac{\mathrm{10}+\mathrm{12}{i}}{\mathrm{10}}×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{244}}{\mathrm{100}×\mathrm{4}}=\frac{\mathrm{61}}{\mathrm{100}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com