Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 37751 by ajfour last updated on 17/Jun/18

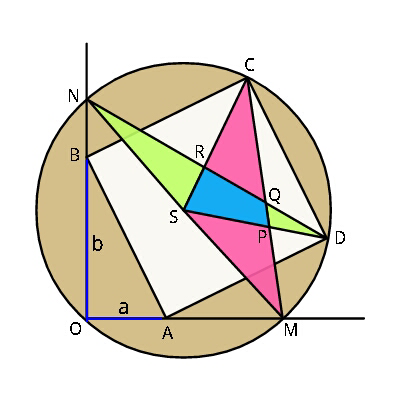
Commented by ajfour last updated on 17/Jun/18

Find area of quadrilateral PQRS in terms of a, b. ABCD is a square.

$${Find}\:{area}\:{of}\:{quadrilateral}\:{PQRS} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{a}},\:\boldsymbol{{b}}. \\ $$$${ABCD}\:{is}\:{a}\:{square}. \\ $$

Commented by MJS last updated on 17/Jun/18

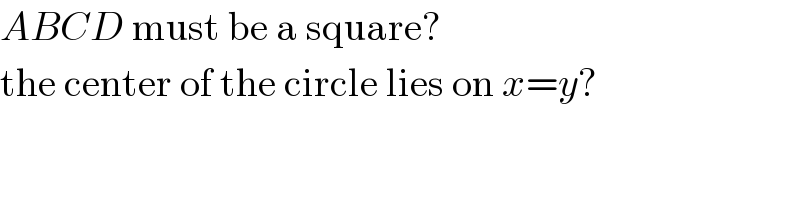
ABCD must be a square? the center of the circle lies on x=y?

$${ABCD}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{square}? \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{lies}\:\mathrm{on}\:{x}={y}? \\ $$

Commented by ajfour last updated on 17/Jun/18

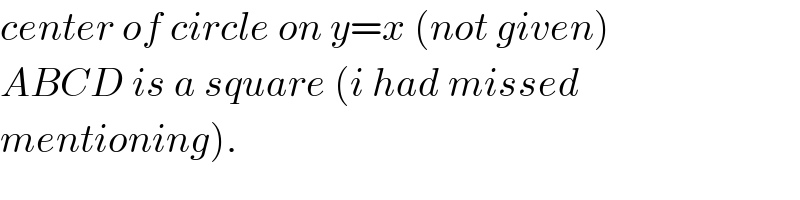
center of circle on y=x (not given) ABCD is a square (i had missed mentioning).

$${center}\:{of}\:{circle}\:{on}\:{y}={x}\:\left({not}\:{given}\right) \\ $$$${ABCD}\:{is}\:{a}\:{square}\:\left({i}\:{had}\:{missed}\right. \\ $$$$\left.{mentioning}\right). \\ $$

Commented by MJS last updated on 17/Jun/18

ok thank you

$$\mathrm{ok}\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by ajfour last updated on 17/Jun/18

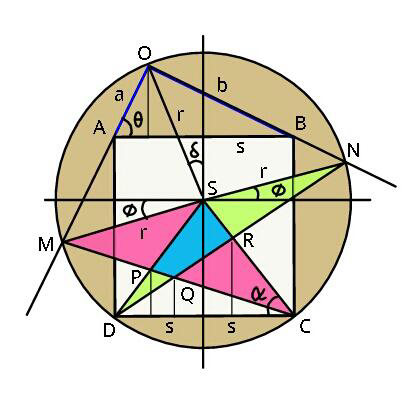
Commented by ajfour last updated on 17/Jun/18

solution part 2_(−) (refer diagram with circle center as origin) let side of square=2s=2rcos α 4s^2 =a^2 +b^2 ....(i) and radius of circle=r angles as marked in figure above. Area_(PQRS) =A A=A_(△SDC) −(A_(△PDC) +A_(△DCR) −A_(△QDC) ) =s[Rsin α−(Rsin α+y_P +Rsin α+y_R ) +Rsin α+y_Q ] ⇒ A=s(y_Q −y_P −y_R ) .....(ii) M≡(−rcos φ, −rsin φ) N≡(rcos φ, rsin φ) C≡(rcos α,−rsin α) D(−rcos α,−rsin α) to evaluate y_P : [rcos α−y_P (((cos α)/(sin α)))]tan ((α/2)−(φ/2)) = rsin α+y_P y_P =((rcos αtan ((α/2)−(φ/2))−rsin α)/(1+(((cos α)/(sin α)))tan ((α/2)−(φ/2)))) to find y_R : [rcos α−y_R (((cos α)/(sin α)))]tan ((α/2)+(φ/2)) = rsin α+y_R y_R =((rcos αtan ((α/2)+(φ/2))−rsin α)/(1+(((cos α)/(sin α)))tan ((α/2)+(φ/2)))) for y_Q : 2rcos α=(rsin α+y_Q )[cot ((α/2)−(φ/2))+cot ((α/2)+(φ/2))] y_Q =((2rcos α)/([cot ((α/2)−(φ/2))+cot ((α/2)+(φ/2))]))−rsin α ....... with rcos α = s = ((√(a^2 +b^2 ))/2) rsin α = (√(r^2 −(((a^2 +b^2 )/4)))) tan θ = (b/a) ⇒ asin θ = ((ab)/(√(a^2 +b^2 ))) acos θ = (a^2 /(√(a^2 +b^2 ))) tan 𝛅 =((rcos 𝛂−acos 𝛉)/(asin 𝛉+r(2cos 𝛂−sin 𝛂))) 𝛉−𝛗 = (𝛑/2)−𝛉+𝛅 ⇒ 𝛗=2𝛉−𝛅−(𝛑/2) . ( just a plan) ! if a=b , r=((5(√2) a)/6) ; θ=(π/4) 𝛗=𝛅 = 0 ; rcos α =(a/(√2)) ⇒ cos α = (3/5) sin α = (4/5) ; tan (α/2) = (1/2) y_P = −((10(√2) a)/(33)) =y_R y_Q = −((5a(√2))/(12)) A = (a^2 /(√2))(((20(√2))/(33))−((5(√2))/(12))) = ((75a^2 )/(33×12)) (A_(PQRS) )∣_(a=b) = ((25a^2 )/(132)) .

$$\underset{−} {{solution}\:{part}\:\mathrm{2}}\:\left({refer}\:{diagram}\:\right. \\ $$$$\left.{with}\:{circle}\:{center}\:{as}\:{origin}\right) \\ $$$${let}\:{side}\:{of}\:{square}=\mathrm{2}\boldsymbol{{s}}=\mathrm{2}{r}\mathrm{cos}\:\alpha \\ $$$$\mathrm{4}{s}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\:\:\:\:....\left({i}\right) \\ $$$${and}\:{radius}\:{of}\:{circle}=\boldsymbol{{r}} \\ $$$${angles}\:{as}\:{marked}\:{in}\:{figure}\:{above}. \\ $$$${Area}_{{PQRS}} ={A} \\ $$$$\boldsymbol{{A}}={A}_{\bigtriangleup{SDC}} −\left({A}_{\bigtriangleup{PDC}} +{A}_{\bigtriangleup{DCR}} −{A}_{\bigtriangleup{QDC}} \right) \\ $$$$\:\:=\boldsymbol{{s}}\left[{R}\mathrm{sin}\:\alpha−\left({R}\mathrm{sin}\:\alpha+{y}_{{P}} +{R}\mathrm{sin}\:\alpha+{y}_{{R}} \right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{R}\mathrm{sin}\:\alpha+{y}_{{Q}} \:\right] \\ $$$$\Rightarrow\:\:\:{A}={s}\left({y}_{{Q}} −{y}_{{P}} −{y}_{{R}} \right)\:\:\:.....\left({ii}\right) \\ $$$${M}\equiv\left(−{r}\mathrm{cos}\:\phi,\:−{r}\mathrm{sin}\:\phi\right) \\ $$$${N}\equiv\left({r}\mathrm{cos}\:\phi,\:{r}\mathrm{sin}\:\phi\right) \\ $$$${C}\equiv\left({r}\mathrm{cos}\:\alpha,−{r}\mathrm{sin}\:\alpha\right) \\ $$$${D}\left(−{r}\mathrm{cos}\:\alpha,−{r}\mathrm{sin}\:\alpha\right) \\ $$$${to}\:{evaluate}\:\boldsymbol{{y}}_{\boldsymbol{{P}}} \:: \\ $$$$\left[{r}\mathrm{cos}\:\alpha−{y}_{{P}} \left(\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\right)\right]\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}−\frac{\phi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:=\:{r}\mathrm{sin}\:\alpha+{y}_{{P}} \\ $$$${y}_{{P}} =\frac{{r}\mathrm{cos}\:\alpha\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}−\frac{\phi}{\mathrm{2}}\right)−{r}\mathrm{sin}\:\alpha}{\mathrm{1}+\left(\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\right)\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}−\frac{\phi}{\mathrm{2}}\right)} \\ $$$${to}\:{find}\:\boldsymbol{{y}}_{\boldsymbol{{R}}} \:: \\ $$$$\left[{r}\mathrm{cos}\:\alpha−{y}_{{R}} \left(\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\right)\right]\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\phi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{r}\mathrm{sin}\:\alpha+{y}_{{R}} \\ $$$${y}_{{R}} =\frac{{r}\mathrm{cos}\:\alpha\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\phi}{\mathrm{2}}\right)−{r}\mathrm{sin}\:\alpha}{\mathrm{1}+\left(\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\right)\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\phi}{\mathrm{2}}\right)} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{y}}_{\boldsymbol{{Q}}} \:: \\ $$$$\mathrm{2}{r}\mathrm{cos}\:\alpha=\left({r}\mathrm{sin}\:\alpha+{y}_{{Q}} \right)\left[\mathrm{cot}\:\left(\frac{\alpha}{\mathrm{2}}−\frac{\phi}{\mathrm{2}}\right)+\mathrm{cot}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\phi}{\mathrm{2}}\right)\right] \\ $$$${y}_{{Q}} =\frac{\mathrm{2}{r}\mathrm{cos}\:\alpha}{\left[\mathrm{cot}\:\left(\frac{\alpha}{\mathrm{2}}−\frac{\phi}{\mathrm{2}}\right)+\mathrm{cot}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\phi}{\mathrm{2}}\right)\right]}−{r}\mathrm{sin}\:\alpha \\ $$$$....... \\ $$$${with}\:\:{r}\mathrm{cos}\:\alpha\:=\:{s}\:=\:\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{r}\mathrm{sin}\:\alpha\:=\:\sqrt{{r}^{\mathrm{2}} −\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{4}}\right)}\: \\ $$$$\:\:\mathrm{tan}\:\theta\:=\:\frac{{b}}{{a}}\:\:\Rightarrow\:\:{a}\mathrm{sin}\:\theta\:=\:\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${a}\mathrm{cos}\:\theta\:=\:\frac{{a}^{\mathrm{2}} }{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\: \\ $$$$\mathrm{tan}\:\boldsymbol{\delta}\:=\frac{\boldsymbol{{r}}\mathrm{cos}\:\boldsymbol{\alpha}−\boldsymbol{{a}}\mathrm{cos}\:\boldsymbol{\theta}}{\boldsymbol{{a}}\mathrm{sin}\:\boldsymbol{\theta}+\boldsymbol{{r}}\left(\mathrm{2cos}\:\boldsymbol{\alpha}−\mathrm{sin}\:\boldsymbol{\alpha}\right)} \\ $$$$\boldsymbol{\theta}−\boldsymbol{\phi}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}−\boldsymbol{\theta}+\boldsymbol{\delta} \\ $$$$\Rightarrow\:\:\:\boldsymbol{\phi}=\mathrm{2}\boldsymbol{\theta}−\boldsymbol{\delta}−\frac{\boldsymbol{\pi}}{\mathrm{2}}\:\:. \\ $$$$\left(\:{just}\:{a}\:{plan}\right)\:! \\ $$$${if}\:{a}={b}\:\:,\:\:\:{r}=\frac{\mathrm{5}\sqrt{\mathrm{2}}\:{a}}{\mathrm{6}}\:\:;\:\:\theta=\frac{\pi}{\mathrm{4}}\: \\ $$$$\boldsymbol{\phi}=\boldsymbol{\delta}\:=\:\mathrm{0}\:;\:\: \\ $$$${r}\mathrm{cos}\:\alpha\:=\frac{{a}}{\sqrt{\mathrm{2}}}\:\Rightarrow\:\:\:\:\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{sin}\:\alpha\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:\:;\:\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}_{{P}} =\:−\frac{\mathrm{10}\sqrt{\mathrm{2}}\:{a}}{\mathrm{33}}\:\:={y}_{{R}} \\ $$$${y}_{{Q}} \:=\:−\frac{\mathrm{5}{a}\sqrt{\mathrm{2}}}{\mathrm{12}} \\ $$$${A}\:=\:\frac{{a}^{\mathrm{2}} }{\sqrt{\mathrm{2}}}\left(\frac{\mathrm{20}\sqrt{\mathrm{2}}}{\mathrm{33}}−\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{12}}\right)\:=\:\frac{\mathrm{75}{a}^{\mathrm{2}} }{\mathrm{33}×\mathrm{12}} \\ $$$$\:\:\:\:\left({A}_{{PQRS}} \right)\mid_{{a}={b}} =\:\frac{\mathrm{25}{a}^{\mathrm{2}} }{\mathrm{132}}\:. \\ $$

Commented by MJS last updated on 17/Jun/18

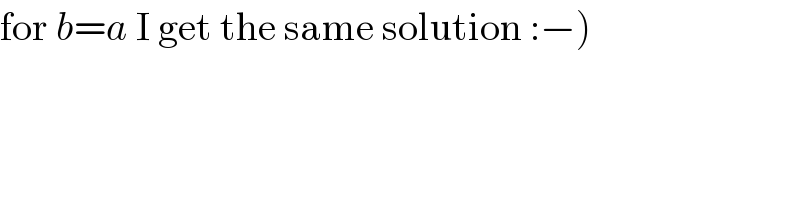
for b=a I get the same solution :−)

$$\left.\mathrm{for}\:{b}={a}\:\mathrm{I}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{solution}\::−\right) \\ $$

Commented by ajfour last updated on 17/Jun/18

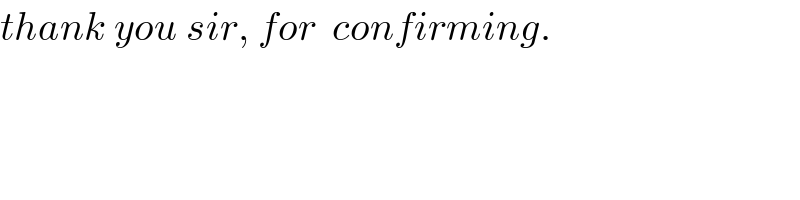
thank you sir, for confirming.

$${thank}\:{you}\:{sir},\:{for}\:\:{confirming}. \\ $$

Answered by ajfour last updated on 17/Jun/18

Refer to diagram in question:_(−) solution part 1_(−) let circle center be (h,k) h^2 +k^2 =r^2 (as circle passes through origin) here we take O as origin; later circle center as origin in the commented diagram. C(b,a+b) ; D(a+b,a) eq. of circle : 2hx+2ky = x^2 +y^2 C and D lies on circle, So 2bh+2(a+b)k=b^2 +(a+b)^2 2(a+b)h+2ak=(a+b)^2 +a^2 2h = ((a[b^2 +(a+b)^2 ]−(a+b)[(a+b)^2 +a^2 ])/(ab−(a+b)^2 )) 2k= ((b[(a+b)^2 +a^2 ]−(a+b)[(a+b)^2 +a^2 ])/(ab−(a+b)^2 )) r^2 =h^2 +k^2 . [if a=b we have h=k= ((5a)/6) and r=((5(√2) a)/6) ].

$$\underset{−} {{Refer}\:{to}\:{diagram}\:{in}\:{question}:} \\ $$$$\underset{−} {{solution}\:\:{part}\:\mathrm{1}} \\ $$$${let}\:{circle}\:{center}\:{be}\:\left({h},{k}\right) \\ $$$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:\left({as}\:{circle}\:{passes}\:{through}\:{origin}\right) \\ $$$${here}\:{we}\:{take}\:{O}\:{as}\:{origin}; \\ $$$${later}\:{circle}\:{center}\:{as}\:{origin}\:{in} \\ $$$${the}\:{commented}\:{diagram}. \\ $$$${C}\left({b},{a}+{b}\right)\:\:\:;\:\:{D}\left({a}+{b},{a}\right) \\ $$$${eq}.\:{of}\:{circle}\:: \\ $$$$\mathrm{2}{hx}+\mathrm{2}{ky}\:=\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${C}\:{and}\:{D}\:{lies}\:{on}\:{circle},\:{So} \\ $$$$\mathrm{2}\boldsymbol{{bh}}+\mathrm{2}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\boldsymbol{{k}}=\boldsymbol{{b}}^{\mathrm{2}} +\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\boldsymbol{{h}}+\mathrm{2}\boldsymbol{{ak}}=\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} \\ $$$$\mathrm{2}{h}\:=\:\frac{{a}\left[{b}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} \right]−\left({a}+{b}\right)\left[\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right]}{{ab}−\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}{k}=\:\frac{{b}\left[\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right]−\left({a}+{b}\right)\left[\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right]}{{ab}−\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\boldsymbol{{r}}^{\mathrm{2}} =\boldsymbol{{h}}^{\mathrm{2}} +\boldsymbol{{k}}^{\mathrm{2}} \:. \\ $$$$\left[{if}\:{a}={b}\:\:\:\:{we}\:{have}\:{h}={k}=\:\frac{\mathrm{5}{a}}{\mathrm{6}}\:\right. \\ $$$$\left.\:\:\:\:\:{and}\:\:\:{r}=\frac{\mathrm{5}\sqrt{\mathrm{2}}\:{a}}{\mathrm{6}}\:\right]. \\ $$

Answered by MJS last updated on 17/Jun/18

I took the first picture you posted... A= ((a),(0) ) B= ((0),(b) ) C= ((b),((a+b)) ) D= (((a+b)),(a) ) ∣SO∣=∣SC∣=∣SD∣ ⇒ ⇒ S= (((((a+b)^3 −ab(a+2b))/(2((a+b)^2 −ab)))),((((a+b)^3 −ab(2a+b))/(2((a+b)^2 −ab)))) ) ⇒ r=((√((a^2 +b^2 )((a+b)^4 +((a+b)^2 −ab)^2 )))/(2((a+b)^2 −ab))) ⇒ M= (((((a+b)^3 −ab(a+2b))/((a+b)^2 −ab))),(0) ) N= ((0),((((a+b)^3 −ab(2a+b))/((a+b)^2 −ab))) ) P=CM∩DS P= ((((((a+b)^2 −ab)((a+b)^2 +ab))/((a+b)^3 +a((a+b)^2 −ab)))),(((a(a+b)((a+b)^2 +b^2 ))/((a+b)^3 +a((a+b)^2 −ab)))) ) Q=CM∩DN Q= ((((b((a+b)^2 +a^2 ))/((a+b)^2 ))),(((a((a+b)^2 +b^2 ))/((a+b)^2 ))) ) R=CS∩DN R= ((((b(a+b)((a^2 +b^2 )+a^2 ))/((a+b)^3 +b((a+b)^2 −ab)))),(((((a+b)^2 −ab)((a+b)^2 +ab))/((a+b)^3 +b((a+b)^2 −ab)))) ) area(PQRS)=area(CPS)−area(CQR)= =((b(a+b)^2 (a^2 +b^2 )((a+b)^2 +a^2 ))/(4((a+b)^2 −ab)((a+b)^2 (2a+b)−a^2 b)))− −((b^3 (a^2 +b^2 )((a+b)^2 +a^2 ))/(2(a+b)^2 ((a+b)^2 (a+2b)−ab^2 )))= =((ab(a^2 +b^2 )(2(a+b)^8 +2ab(a+b)^6 −7a^2 b^2 (a+b)^4 +6a^3 b^3 (a+b)^2 −2a^4 b^4 ))/(4(a+b)^2 ((a+b)^2 −ab)((a+b)^3 +a((a+b)^2 −ab))((a+b)^3 +b((a+b)^2 −ab))))=

$$\mathrm{I}\:\mathrm{took}\:\mathrm{the}\:\mathrm{first}\:\mathrm{picture}\:\mathrm{you}\:\mathrm{posted}... \\ $$$$ \\ $$$${A}=\begin{pmatrix}{{a}}\\{\mathrm{0}}\end{pmatrix}\:{B}=\begin{pmatrix}{\mathrm{0}}\\{{b}}\end{pmatrix}\:{C}=\begin{pmatrix}{{b}}\\{{a}+{b}}\end{pmatrix}\:{D}=\begin{pmatrix}{{a}+{b}}\\{{a}}\end{pmatrix} \\ $$$$\mid{SO}\mid=\mid{SC}\mid=\mid{SD}\mid\:\Rightarrow \\ $$$$\Rightarrow\:{S}=\begin{pmatrix}{\frac{\left({a}+{b}\right)^{\mathrm{3}} −{ab}\left({a}+\mathrm{2}{b}\right)}{\mathrm{2}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\\{\frac{\left({a}+{b}\right)^{\mathrm{3}} −{ab}\left(\mathrm{2}{a}+{b}\right)}{\mathrm{2}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\end{pmatrix} \\ $$$$\Rightarrow\:{r}=\frac{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\left({a}+{b}\right)^{\mathrm{4}} +\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)^{\mathrm{2}} \right)}}{\mathrm{2}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)} \\ $$$$\Rightarrow\:{M}=\begin{pmatrix}{\frac{\left({a}+{b}\right)^{\mathrm{3}} −{ab}\left({a}+\mathrm{2}{b}\right)}{\left({a}+{b}\right)^{\mathrm{2}} −{ab}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:{N}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\left({a}+{b}\right)^{\mathrm{3}} −{ab}\left(\mathrm{2}{a}+{b}\right)}{\left({a}+{b}\right)^{\mathrm{2}} −{ab}}}\end{pmatrix} \\ $$$${P}={CM}\cap{DS} \\ $$$${P}=\begin{pmatrix}{\frac{\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\left(\left({a}+{b}\right)^{\mathrm{2}} +{ab}\right)}{\left({a}+{b}\right)^{\mathrm{3}} +{a}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\\{\frac{{a}\left({a}+{b}\right)\left(\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\left({a}+{b}\right)^{\mathrm{3}} +{a}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\end{pmatrix} \\ $$$${Q}={CM}\cap{DN} \\ $$$${Q}=\begin{pmatrix}{\frac{{b}\left(\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{\left({a}+{b}\right)^{\mathrm{2}} }}\\{\frac{{a}\left(\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\left({a}+{b}\right)^{\mathrm{2}} }}\end{pmatrix} \\ $$$${R}={CS}\cap{DN} \\ $$$${R}=\begin{pmatrix}{\frac{{b}\left({a}+{b}\right)\left(\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} \right)}{\left({a}+{b}\right)^{\mathrm{3}} +{b}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\\{\frac{\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\left(\left({a}+{b}\right)^{\mathrm{2}} +{ab}\right)}{\left({a}+{b}\right)^{\mathrm{3}} +{b}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)}}\end{pmatrix} \\ $$$$\mathrm{area}\left({PQRS}\right)=\mathrm{area}\left({CPS}\right)−\mathrm{area}\left({CQR}\right)= \\ $$$$=\frac{{b}\left({a}+{b}\right)^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{\mathrm{4}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\left(\left({a}+{b}\right)^{\mathrm{2}} \left(\mathrm{2}{a}+{b}\right)−{a}^{\mathrm{2}} {b}\right)}− \\ $$$$\:\:\:\:\:−\frac{{b}^{\mathrm{3}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{\mathrm{2}\left({a}+{b}\right)^{\mathrm{2}} \left(\left({a}+{b}\right)^{\mathrm{2}} \left({a}+\mathrm{2}{b}\right)−{ab}^{\mathrm{2}} \right)}= \\ $$$$=\frac{{ab}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{2}\left({a}+{b}\right)^{\mathrm{8}} +\mathrm{2}{ab}\left({a}+{b}\right)^{\mathrm{6}} −\mathrm{7}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{4}} +\mathrm{6}{a}^{\mathrm{3}} {b}^{\mathrm{3}} \left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{4}} {b}^{\mathrm{4}} \right)}{\mathrm{4}\left({a}+{b}\right)^{\mathrm{2}} \left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\left(\left({a}+{b}\right)^{\mathrm{3}} +{a}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\right)\left(\left({a}+{b}\right)^{\mathrm{3}} +{b}\left(\left({a}+{b}\right)^{\mathrm{2}} −{ab}\right)\right)}= \\ $$

Commented by ajfour last updated on 17/Jun/18

Great solution Sir !

$$\mathcal{G}{reat}\:{solution}\:{Sir}\:! \\ $$

Commented by ajfour last updated on 17/Jun/18

was it easy to calculate P = CM∩DS and Q, R ? you show no working Sir ..

$${was}\:{it}\:{easy}\:{to}\:{calculate}\: \\ $$$${P}\:=\:{CM}\cap{DS}\: \\ $$$${and}\:{Q},\:{R}\:?\:{you}\:{show}\:{no}\:{working} \\ $$$${Sir}\:.. \\ $$

Commented by MJS last updated on 18/Jun/18

the method is simple, it′s just finding a line between two points and then intersecting the lines, the only hard work is simplifying. I usually do this by hand because I don′t have any calculator which can properly handle equations of this complexity. you won′t be able to read my scribbling... as you can see at my integral solutions I′m a correct worker and I can show step by step I just decided it′s too hard typing all the equations on my smartphone. sorry for that

$$\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{simple},\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{finding}\:\mathrm{a}\:\mathrm{line} \\ $$$$\mathrm{between}\:\mathrm{two}\:\mathrm{points}\:\mathrm{and}\:\mathrm{then}\:\mathrm{intersecting} \\ $$$$\mathrm{the}\:\mathrm{lines},\:\mathrm{the}\:\mathrm{only}\:\mathrm{hard}\:\mathrm{work}\:\mathrm{is}\:\mathrm{simplifying}. \\ $$$$\mathrm{I}\:\mathrm{usually}\:\mathrm{do}\:\mathrm{this}\:\mathrm{by}\:\mathrm{hand}\:\mathrm{because}\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{have}\:\mathrm{any}\:\mathrm{calculator}\:\mathrm{which}\:\mathrm{can}\:\mathrm{properly} \\ $$$$\mathrm{handle}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{this}\:\mathrm{complexity}. \\ $$$$\mathrm{you}\:\mathrm{won}'\mathrm{t}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{read}\:\mathrm{my}\:\mathrm{scribbling}... \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{at}\:\mathrm{my}\:\mathrm{integral}\:\mathrm{solutions}\:\mathrm{I}'\mathrm{m} \\ $$$$\mathrm{a}\:\mathrm{correct}\:\mathrm{worker}\:\mathrm{and}\:\mathrm{I}\:\mathrm{can}\:\mathrm{show}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{decided}\:\mathrm{it}'\mathrm{s}\:\mathrm{too}\:\mathrm{hard}\:\mathrm{typing}\:\mathrm{all}\:\mathrm{the} \\ $$$$\mathrm{equations}\:\mathrm{on}\:\mathrm{my}\:\mathrm{smartphone}.\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{that} \\ $$

Commented by MJS last updated on 18/Jun/18

my methods: ∣SO∣=∣SC∣=∣SD∣ put S= ((x_S ),(y_S ) ) ∣SO∣^2 =x_S ^2 +y_S ^2 =r^2 ∣SC∣^2 =(x_S −b)^2 +(y_S −(a+b))^2 =r^2 ∣SD∣^2 =(x_S −(a+b))^2 +(y_S −b)^2 =r^2 subtracting two of them to get x_S , y_S without x_S ^2 , y_S ^2 and then solving is the fastest method r=(√(x_S ^2 +y_S ^2 )) S is the center of MN ⇒ M= (((2x_S )),(0) ); N= ((0),((2y_S )) ) P=CM∩DS (and the other 2) line between 2 points: U= ((x_U ),(y_U ) ); V= ((x_V ),(y_V ) ) y=kx+d k=((y_V −y_U )/(x_V −x_U )); d=((x_V y_U −x_U y_V )/(x_V −x_U )) intersection y=k_1 x+d_1 y=k_2 x+d_2 should be obvious now we need the lenghts^2 of the lines CP, CS, PS and CQ, CR, QR ∣UV∣^2 =(x_V −x_U )^2 +(y_V −y_U )^2 the area of the triangles (the hardest part): area(ijk)=((√((i+j+k)(i+j−k)(i+k−j)(j+k−i)))/4)= =((√(2(i^2 j^2 +i^2 k^2 +j^2 k^2 )−(i^4 +j^4 +k^4 )))/4) all you need is 4P: PencilPaperPrecisionPatience

$$\mathrm{my}\:\mathrm{methods}: \\ $$$$\mid{SO}\mid=\mid{SC}\mid=\mid{SD}\mid \\ $$$$\mathrm{put}\:{S}=\begin{pmatrix}{{x}_{{S}} }\\{{y}_{{S}} }\end{pmatrix} \\ $$$$\mid{SO}\mid^{\mathrm{2}} ={x}_{{S}} ^{\mathrm{2}} +{y}_{{S}} ^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mid{SC}\mid^{\mathrm{2}} =\left({x}_{{S}} −{b}\right)^{\mathrm{2}} +\left({y}_{{S}} −\left({a}+{b}\right)\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mid{SD}\mid^{\mathrm{2}} =\left({x}_{{S}} −\left({a}+{b}\right)\right)^{\mathrm{2}} +\left({y}_{{S}} −{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{subtracting}\:\mathrm{two}\:\mathrm{of}\:\mathrm{them}\:\mathrm{to}\:\mathrm{get}\:{x}_{{S}} ,\:{y}_{{S}} \:\mathrm{without}\: \\ $$$${x}_{{S}} ^{\mathrm{2}} ,\:{y}_{{S}} ^{\mathrm{2}} \:\mathrm{and}\:\mathrm{then}\:\mathrm{solving}\:\mathrm{is}\:\mathrm{the}\:\mathrm{fastest}\:\mathrm{method} \\ $$$$ \\ $$$${r}=\sqrt{{x}_{{S}} ^{\mathrm{2}} +{y}_{{S}} ^{\mathrm{2}} } \\ $$$$ \\ $$$${S}\:\mathrm{is}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:{MN}\:\Rightarrow\:{M}=\begin{pmatrix}{\mathrm{2}{x}_{{S}} }\\{\mathrm{0}}\end{pmatrix};\:{N}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{2}{y}_{{S}} }\end{pmatrix} \\ $$$$ \\ $$$${P}={CM}\cap{DS}\:\left(\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{line}\:\mathrm{between}\:\mathrm{2}\:\mathrm{points}: \\ $$$${U}=\begin{pmatrix}{{x}_{{U}} }\\{{y}_{{U}} }\end{pmatrix};\:{V}=\begin{pmatrix}{{x}_{{V}} }\\{{y}_{{V}} }\end{pmatrix} \\ $$$${y}={kx}+{d} \\ $$$${k}=\frac{{y}_{{V}} −{y}_{{U}} }{{x}_{{V}} −{x}_{{U}} };\:{d}=\frac{{x}_{{V}} {y}_{{U}} −{x}_{{U}} {y}_{{V}} }{{x}_{{V}} −{x}_{{U}} } \\ $$$$\mathrm{intersection} \\ $$$${y}={k}_{\mathrm{1}} {x}+{d}_{\mathrm{1}} \\ $$$${y}={k}_{\mathrm{2}} {x}+{d}_{\mathrm{2}} \\ $$$$\mathrm{should}\:\mathrm{be}\:\mathrm{obvious} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{lenghts}^{\mathrm{2}} \:\mathrm{of}\:\mathrm{the}\:\mathrm{lines} \\ $$$${CP},\:{CS},\:{PS}\:\mathrm{and}\:{CQ},\:{CR},\:{QR} \\ $$$$\mid{UV}\mid^{\mathrm{2}} =\left({x}_{{V}} −{x}_{{U}} \right)^{\mathrm{2}} +\left({y}_{{V}} −{y}_{{U}} \right)^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangles}\:\left(\mathrm{the}\:\mathrm{hardest}\:\mathrm{part}\right): \\ $$$$\mathrm{area}\left({ijk}\right)=\frac{\sqrt{\left({i}+{j}+{k}\right)\left({i}+{j}−{k}\right)\left({i}+{k}−{j}\right)\left({j}+{k}−{i}\right)}}{\mathrm{4}}= \\ $$$$=\frac{\sqrt{\mathrm{2}\left({i}^{\mathrm{2}} {j}^{\mathrm{2}} +{i}^{\mathrm{2}} {k}^{\mathrm{2}} +{j}^{\mathrm{2}} {k}^{\mathrm{2}} \right)−\left({i}^{\mathrm{4}} +{j}^{\mathrm{4}} +{k}^{\mathrm{4}} \right)}}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{all}\:\mathrm{you}\:\mathrm{need}\:\mathrm{is}\:\mathrm{4P}: \\ $$$$\mathrm{PencilPaperPrecisionPatience} \\ $$

Commented by ajfour last updated on 18/Jun/18

Too good Sir, thanks a lot.

$${Too}\:{good}\:{Sir},\:{thanks}\:{a}\:{lot}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com