Question Number 37784 by prof Abdo imad last updated on 17/Jun/18
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{dx}}{\mathrm{2}{cosx}\:+{cos}\left(\mathrm{2}{x}\right)} \\ $$
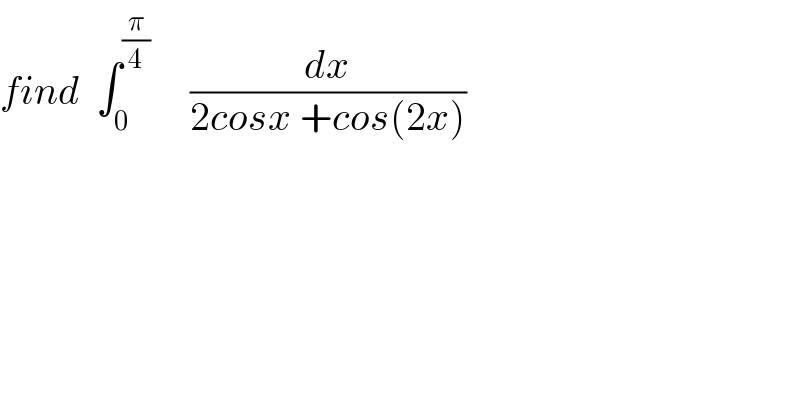
Commented by math khazana by abdo last updated on 18/Jun/18
![I = ∫_0 ^(π/4) (dx/(2cosx +2 cos^2 x−1)) =∫_0 ^(π/4) (dx/(2cos^2 x +2cosx −1)) let decompose F(x)= (1/(2x^2 +2x −1)) Δ^′ =1+2=3 ⇒x_1 =((−1+(√3))/2) and x_2 =((−1−(√3))/2) ⇒ F(x)= (1/(2(x−x_1 )(x−x_2 ))) =(a/(x−x_1 )) +(b/(x−x_2 )) a= (1/(2(x_1 −x_2 ))) =(1/(2.(√3))) b= (1/(2(x_2 −x_1 ))) = (1/(2(−(√3)))) =−(1/(2(√3))) ⇒ F(x)= (1/(2(√3))){ (1/(x −((−1+(√3))/2))) −(1/(x−((−1−(√3))/2)))} = (1/(2(√3))){ (2/(2x+1−(√3))) − (2/(2x +1+(√3)))} ⇒ I = (1/(√3)) ∫_0 ^(π/4) (dx/(2cosx +1−(√3))) −(1/(√3))∫_0 ^(π/4) (dx/(2cosx +1+(√3))) =H −K changement tan((x/2))=t give H = (1/(√3)) ∫_0 ^((√2)−1) (1/(2((1−t^2 )/(1+t^2 )) +1−(√3))) ((2dt)/(1+t^2 )) = (2/(√3)) ∫_0 ^((√2)−1) (dt/(2−2t^2 +1−(√3) +(1−(√3))t^2 )) =(2/(√3)) ∫_0 ^((√2)−1) (dt/(3−(√3) −(1+(√3))t^2 )) =(2/((√3)(3−(√3)))) ∫_0 ^((√2)−1) (dt/(1−((√((1+(√3))/(3−(√3))))t)^2 )) =_((√((1+(√3))/(3−(√3))))t=u) (2/((√3)(3−(√3)))) ∫_0 ^(((√2)−1)(√((1+(√3))/(3−(√3))))) (1/(1−u^2 )) (√((3−(√3))/(1+(√3))))du = (2/((√3)(√((3−(√(3)(1+(√(3))))))))) ∫_0 ^(((√(2−1)))(√((1+(√3))/(3−(√3))))) (du/(1−u^2 )) = (1/((√3)(√((3−(√3))(1+(√3))))))[ln∣ ((1+u)/(1−u))∣]_0 ^(((√2)−1)(√((1+(√3))/(3−(√3))))) = ((√3)/(3(√((3−(√3))(1+(√3))))))ln( ((1+λ)/(1−λ))) with λ= ((√2)−1)(√((1+(√3))/(3−(√3)))) we follow the same?method to calculate K....](Q37835.png)
$$\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{dx}}{\mathrm{2}{cosx}\:+\mathrm{2}\:{cos}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} {x}\:+\mathrm{2}{cosx}\:−\mathrm{1}}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:−\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{1}+\mathrm{2}=\mathrm{3}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:{and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)}\:=\frac{{a}}{{x}−{x}_{\mathrm{1}} }\:+\frac{{b}}{{x}−{x}_{\mathrm{2}} } \\ $$$${a}=\:\frac{\mathrm{1}}{\mathrm{2}\left({x}_{\mathrm{1}} \:−{x}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}.\sqrt{\mathrm{3}}} \\ $$$${b}=\:\frac{\mathrm{1}}{\mathrm{2}\left({x}_{\mathrm{2}} \:−{x}_{\mathrm{1}} \right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(−\sqrt{\mathrm{3}}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left\{\:\:\frac{\mathrm{1}}{{x}\:−\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}}\:\:−\frac{\mathrm{1}}{{x}−\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}}\right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left\{\:\:\:\frac{\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}−\sqrt{\mathrm{3}}}\:−\:\frac{\mathrm{2}}{\mathrm{2}{x}\:+\mathrm{1}+\sqrt{\mathrm{3}}}\right\}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\:\frac{{dx}}{\mathrm{2}{cosx}\:+\mathrm{1}−\sqrt{\mathrm{3}}}\:−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\mathrm{2}{cosx}\:+\mathrm{1}+\sqrt{\mathrm{3}}} \\ $$$$={H}\:−{K} \\ $$$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${H}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{1}−\sqrt{\mathrm{3}}}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\:\:\:\frac{{dt}}{\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}−\sqrt{\mathrm{3}}\:+\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\:\frac{{dt}}{\mathrm{3}−\sqrt{\mathrm{3}}\:\:−\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}−\left(\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}}{t}\right)^{\mathrm{2}} } \\ $$$$=_{\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}}{t}={u}} \:\:\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}\:\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\sqrt{\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{3}}}}{du} \\ $$$$=\:\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}\sqrt{\left(\mathrm{3}−\sqrt{\left.\mathrm{3}\right)\left(\mathrm{1}+\sqrt{\left.\mathrm{3}\right)}\right.}\right.}}\:\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}−\mathrm{1}}\right)\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}}} \:\:\:\:\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\sqrt{\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}}\left[{ln}\mid\:\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}}} \\ $$$$=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}}{ln}\left(\:\:\:\frac{\mathrm{1}+\lambda}{\mathrm{1}−\lambda}\right)\:{with} \\ $$$$\lambda=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}−\sqrt{\mathrm{3}}}} \\ $$$${we}\:{follow}\:{the}\:{same}?{method}\:{to}\:{calculate}\:{K}.... \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{\mathrm{2}{cosx}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{{cos}^{\mathrm{2}} {x}+{cosx}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}^{\mathrm{2}} +{a}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}.{a}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left({a}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\left({a}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right) \\ $$$$\left({a}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\left({a}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right) \\ $$$$\left({a}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)−\left({a}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right) \\ $$$$\sqrt{\mathrm{3}}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{\sqrt{\mathrm{3}}\:}{\left({cosx}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\left({cosx}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}\:}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{{cosx}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{{cosx}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}\:}\left\{\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{{a}+{cosx}}−\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{dx}}{{b}+{cosx}}\right\} \\ $$$${now}\:{it}\:{can}\:{be}\:{solved}\:{but}\:{lenthy}...{method}...\int \\ $$$$\int\frac{{dx}}{{a}+{cosx}} \\ $$$$\int\frac{{dx}}{{a}+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{a}+{atan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\left({a}+\mathrm{1}\right)+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\left({a}−\mathrm{1}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{a}−\mathrm{1}}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:\:{dt}={sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}{dx} \\ $$$$\frac{\mathrm{2}}{{a}−\mathrm{1}}\int\frac{{dt}}{\left\{\sqrt{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}\:}\:\right\}^{\mathrm{2}} +{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{{a}−\mathrm{1}}×\frac{\sqrt{{a}−\mathrm{1}}\:\:}{\sqrt{{a}+\mathrm{1}}}\:×{tan}^{−\mathrm{1}} \left\{\frac{{t}}{\frac{\sqrt{{a}−\mathrm{1}}\:}{\sqrt{{a}+\mathrm{1}}}}\right\}...{like}\:{this}\:{way} \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 17/Jun/18
![Weierstrass ∫(dx/(2cos x +cos 2x))= [t=tan (x/2) → dx=((2dt)/(1+t^2 ))] =−2∫((t^2 +1)/(t^4 +6t^2 −3))dt= =−2∫((t^2 +1)/((t−(√(−3+2(√3))))(t+(√(−3+2(√3))))(t^2 +3+2(√3))))dt= =−2(∫(A/(t−(√(−3+2(√3)))))dt+∫(B/(t+(√(−3+2(√3)))))dt+∫(C/(t^2 +3+2(√3)))dt)= =−((√(2(√3)))/6)∫(dt/(t−(√(−3+2(√3)))))+((√(2(√3)))/6)∫(dt/(t+(√(−3+2(√3)))))−((3+(√3))/3)∫(dt/(t^2 +3+2(√3))))= [∫(dx/(x±a))=ln∣x±a∣; ∫(dx/(x^2 +a))=(1/(√a))arctan (x/(√a))] =((√(2(√3)))/6)(ln∣t+(√(−3+2(√3)))∣−ln∣t−(√(−3+2(√3)))∣)−(1+((√3)/3))(1/(√(3+2(√3))))arctan (t/(√(3+2(√3))))= =((√(2(√3)))/6)ln∣((t+(√(−3+2(√3))))/(t−(√(−3+2(√3)))))∣ −((√(2(√3)))/3)arctan (((√(2(√3)))(3−(√3))t)/6)= =((√(2(√3)))/6)(ln∣((t+(√(−3+2(√3))))/(t−(√(−3+2(√3)))))∣ −2arctan (((√(2(√3)))(3−(√3))t)/6))= =((√(2(√3)))/6)(ln∣((tan (x/2)+(√(−3+2(√3))))/(tan (x/2)−(√(−3+2(√3)))))∣ −2arctan (((√(2(√3)))(3−(√3))tan (x/2))/6))+C](Q37825.png)
$$\mathrm{Weierstrass} \\ $$$$\int\frac{{dx}}{\mathrm{2cos}\:{x}\:+\mathrm{cos}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{6}{t}^{\mathrm{2}} −\mathrm{3}}{dt}= \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\right)\left({t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\right)\left({t}^{\mathrm{2}} +\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=−\mathrm{2}\left(\int\frac{\mathcal{A}}{{t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{dt}+\int\frac{\mathcal{B}}{{t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{dt}+\int\frac{\mathcal{C}}{{t}^{\mathrm{2}} +\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{dt}\right)= \\ $$$$\left.=−\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\int\frac{{dt}}{{t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}+\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\int\frac{{dt}}{{t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}−\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\int\frac{{dx}}{{x}\pm{a}}=\mathrm{ln}\mid{x}\pm{a}\mid;\:\int\frac{{dx}}{{x}^{\mathrm{2}} +{a}}=\frac{\mathrm{1}}{\sqrt{{a}}}\mathrm{arctan}\:\frac{{x}}{\sqrt{{a}}}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\left(\mathrm{ln}\mid{t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mid−\mathrm{ln}\mid{t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}\mid\right)−\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\frac{\mathrm{1}}{\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mathrm{arctan}\:\frac{{t}}{\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}= \\ $$$$=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\mathrm{ln}\mid\frac{{t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{{t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid\:−\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right){t}}{\mathrm{6}}= \\ $$$$=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\left(\mathrm{ln}\mid\frac{{t}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{{t}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid\:−\mathrm{2arctan}\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right){t}}{\mathrm{6}}\right)= \\ $$$$=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{6}}\left(\mathrm{ln}\mid\frac{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}+\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}−\sqrt{−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}}\mid\:−\mathrm{2arctan}\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}{\mathrm{6}}\right)+{C} \\ $$
Commented by math khazana by abdo last updated on 18/Jun/18
$${good}\:{hard}\:{work} \\ $$