Question Number 37862 by ajfour last updated on 18/Jun/18
Commented by MrW3 last updated on 18/Jun/18
$${yes},\:\sqrt{{r}^{\mathrm{2}} +{q}^{\mathrm{2}} }<\mathrm{2}{a}. \\ $$
Commented by ajfour last updated on 18/Jun/18
$$\sqrt{{r}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:<\:\mathrm{2}{b}\:. \\ $$
Commented by ajfour last updated on 18/Jun/18
$${With}\:{the}\:{help}\:{of}\:{some}\:{app},\:{can} \\ $$$${anyone}\:{share}\:{and}\:{show}\:{us}\:{the} \\ $$$${locus}\:{trajectory},\:{please}\:? \\ $$
Commented by Rio Mike last updated on 18/Jun/18
$${sir}\:{ajfour}\:{what}\:{app}\:{do}\:{you}\: \\ $$$${guys}\:{use}\:{in}\:{drawing}\:{the}\:{shapes} \\ $$$${you}\:{always}\:{post}? \\ $$
Commented by ajfour last updated on 18/Jun/18
$${i}\:{do}\:{so}\:{using}\:{Lekh}\:{Diagram}. \\ $$
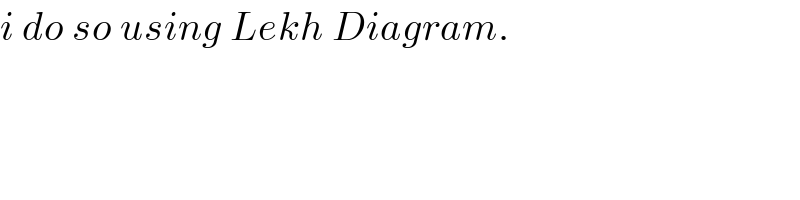
Commented by MrW3 last updated on 18/Jun/18
$${it}\:{should}\:{be}\:\sqrt{{r}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:>\:\mathrm{2}{b}\:. \\ $$
Commented by ajfour last updated on 18/Jun/18
$${only}\:\sqrt{{r}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:<\:\mathrm{2}{a}\:{is}\:{necessary}, \\ $$$${dont}\:{you}\:{think}\:{so},\:{Sir}\:? \\ $$
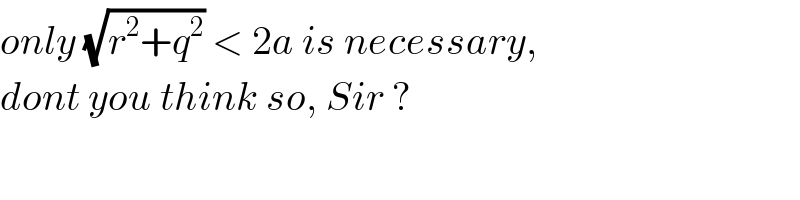
Answered by ajfour last updated on 18/Jun/18
![let P ≡ (x,y) and x_Q = x+rcos θ y_Q = y+rsin θ then x_R = x−qsin θ y_R = y+qcos θ As Q and R lie on ellipse , so (((x+rcos θ)^2 )/a^2 )+(((y+rsin θ)^2 )/b^2 )=1 (((x−qsin θ)^2 )/a^2 )+(((y+qcos θ)^2 )/b^2 )=1 We now need to eliminate θ and thus relate x, y . ⇒ q, r are roots of eq. (((x−zsin θ)^2 )/a^2 )+(((y+zcos θ)^2 )/b^2 )=1 ⇒ z^2 (a^2 cos^2 θ+b^2 sin^2 θ) +2z(a^2 ycos θ−b^2 xsin θ) +b^2 x^2 +a^2 y^2 −a^2 b^2 = 0 as q, r are roots of the eq. q+r = −((2(a^2 ycos^2 θ−b^2 xsin^2 θ))/(a^2 cos^2 θ+b^2 sin^2 θ)) qr = ((b^2 x^2 +a^2 y^2 −a^2 b^2 )/(a^2 cos^2 θ+b^2 sin^2 θ)) ....(i) let tan^2 θ = t ⇒ q+r=((−2(a^2 y−b^2 xt))/(a^2 +b^2 t)) or t = ((a^2 (q+r)+2a^2 y)/(b^2 (2x−q−r))) substituting in (i) qr = (((b^2 x^2 +a^2 y^2 −a^2 b^2 )[2b^2 x+2a^2 y+(a^2 −b^2 )(q+r)])/(a^2 b^2 (2x−q−r)+a^2 b^2 (2y+q+r))) ⇒ 2a^2 b^2 qr(x+y)=(b^2 x^2 +a^2 y^2 −a^2 b^2 )× [2b^2 x+2a^2 y+(a^2 −b^2 )(q+r)] .](Q37873.png)
$${let}\:{P}\:\equiv\:\left({x},{y}\right) \\ $$$${and}\:\:\:{x}_{{Q}} \:=\:{x}+{r}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{y}_{{Q}} \:=\:{y}+{r}\mathrm{sin}\:\theta \\ $$$${then}\:\:\:\:{x}_{{R}} =\:{x}−{q}\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}_{{R}} \:=\:{y}+{q}\mathrm{cos}\:\theta \\ $$$${As}\:{Q}\:{and}\:{R}\:{lie}\:{on}\:{ellipse}\:,\:{so} \\ $$$$\:\:\:\frac{\left({x}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}+{r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\:\frac{\left({x}−{q}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}+{q}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${We}\:{now}\:{need}\:{to}\:{eliminate}\:\theta\:{and} \\ $$$${thus}\:{relate}\:{x},\:{y}\:. \\ $$$$\Rightarrow\:{q},\:{r}\:{are}\:{roots}\:{of}\:{eq}. \\ $$$$\:\:\:\:\frac{\left({x}−{z}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}+{z}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\:{z}^{\mathrm{2}} \left({a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:+\mathrm{2}{z}\left({a}^{\mathrm{2}} {y}\mathrm{cos}\:\theta−{b}^{\mathrm{2}} {x}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:+{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:=\:\mathrm{0} \\ $$$${as}\:{q},\:{r}\:{are}\:{roots}\:{of}\:{the}\:{eq}. \\ $$$${q}+{r}\:=\:−\frac{\mathrm{2}\left({a}^{\mathrm{2}} {y}\mathrm{cos}\:^{\mathrm{2}} \theta−{b}^{\mathrm{2}} {x}\mathrm{sin}\:^{\mathrm{2}} \theta\right)}{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\:{qr}\:=\:\frac{{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\:\:\:\:....\left({i}\right) \\ $$$${let}\:\:\:\mathrm{tan}\:^{\mathrm{2}} \theta\:=\:{t} \\ $$$$\Rightarrow\:{q}+{r}=\frac{−\mathrm{2}\left({a}^{\mathrm{2}} {y}−{b}^{\mathrm{2}} {xt}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {t}} \\ $$$${or}\:\:\:{t}\:=\:\frac{{a}^{\mathrm{2}} \left({q}+{r}\right)+\mathrm{2}{a}^{\mathrm{2}} {y}}{{b}^{\mathrm{2}} \left(\mathrm{2}{x}−{q}−{r}\right)} \\ $$$${substituting}\:{in}\:\left({i}\right) \\ $$$$\:\:{qr}\:=\:\frac{\left({b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)\left[\mathrm{2}{b}^{\mathrm{2}} {x}+\mathrm{2}{a}^{\mathrm{2}} {y}+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({q}+{r}\right)\right]}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{2}{x}−{q}−{r}\right)+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{2}{y}+{q}+{r}\right)} \\ $$$$\Rightarrow\:\:\mathrm{2}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{qr}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)=\left(\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \right)× \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{x}}+\mathrm{2}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{y}}+\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \right)\left(\boldsymbol{{q}}+\boldsymbol{{r}}\right)\right]\:. \\ $$