
Question Number 37888 by abdo mathsup 649 cc last updated on 19/Jun/18
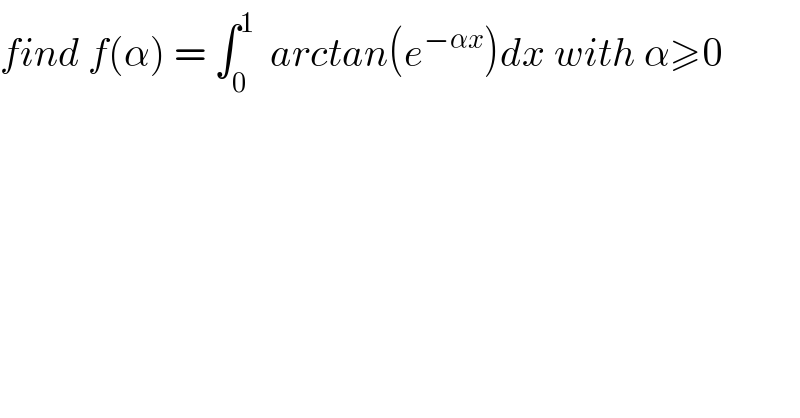
$${find}\:{f}\left(\alpha\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{arctan}\left({e}^{−\alpha{x}} \right){dx}\:{with}\:\alpha\geqslant\mathrm{0}\: \\ $$
Commented by math khazana by abdo last updated on 21/Jun/18
![we have f^′ (α)=∫_0 ^1 ((−x e^(−αx) )/(1+e^(−2αx) ))dx = ∫_0 ^1 −x e^(−αx) { Σ_(n=0) ^∞ (−1)^n e^(−2nαx) } =Σ_(n=0) ^∞ (−1)^(n+1) ∫_0 ^1 x e^(−(2n+1)αx) dx but A_n =∫_0 ^1 x e^(−(2n+1)αx) dx=_((2n+1)αx=t) ∫_0 ^((2n+1)α) (t/((2n+1)α)) e^(−t) (dt/((2n+1)α)) = (1/((2n+1)^2 α^2 )) ∫_0 ^((2n+1)α) t .e^(−t) dt and by parts ∫_0 ^((2n+1)α) t.e^(−t) dt =[−t e^(−t) ]_0 ^((2n+1)α) +∫_0 ^((2n+1)α) e^(−t) dt =−(2n+1)α e^(−(2n+1)α) +[−e^(−t) ]_0 ^((2n+1)α) =−(2n+1)α e^(−(2n+1)α) +(1−e^(−(2n+1)α) ) ⇒ A_n = (1/((2n+1)^2 α^2 )){ −(2n+1)α e^(−(2n+1)α) +(1−e^(−(2n+1)α) ) =−(1/((2n+1)α)) e^(−(2n+1)α) +((1−e^(−(2n+1)α) )/((2n+1)^2 α^2 )) I =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)α)) e^(−(2n+1)α) +Σ_(n=0) ^∞ (−1)^n ((e^(−(2n+1)α) −1)/((2n+1)^2 α^2 )) ...be continued...](Q38088.png)
$${we}\:{have}\:{f}^{'} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−{x}\:{e}^{−\alpha{x}} }{\mathrm{1}+{e}^{−\mathrm{2}\alpha{x}} }{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:−{x}\:{e}^{−\alpha{x}} \left\{\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{2}{n}\alpha{x}} \right\} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}} {dx}\:{but} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}} {dx}=_{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}={t}} \:\int_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\frac{{t}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha}\:{e}^{−{t}} \:\frac{{dt}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \\ $$$$=\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \alpha^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\:{t}\:.{e}^{−{t}} {dt}\:\:{and}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:{t}.{e}^{−{t}} {dt}\:=\left[−{t}\:{e}^{−{t}} \right]_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:+\int_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:{e}^{−{t}} {dt} \\ $$$$=−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\:+\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \\ $$$$=−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:+\left(\mathrm{1}−{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \right)\:\Rightarrow \\ $$$${A}_{{n}} =\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \alpha^{\mathrm{2}} }\left\{\:−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:+\left(\mathrm{1}−{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \right)\right. \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\:\:+\frac{\mathrm{1}−{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \:\alpha^{\mathrm{2}} } \\ $$$${I}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\:+\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \frac{{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:−\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \:\alpha^{\mathrm{2}} } \\ $$$$...{be}\:{continued}... \\ $$
Commented by math khazana by abdo last updated on 21/Jun/18
![we have artan^′ (u)= (1/(1+u^2 )) =Σ_(n=0) ^∞ (−1)^n u^(2n) ⇒ arctan(u) = Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) u^(2n+1) +c (c=0)⇒ arctan(e^(−αx) ) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) e^(−(2n+1)αx) and f(α)= ∫_0 ^1 arctan(e^(−αx) )dx =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) ∫_0 ^1 e^(−(2n+1)αx) dx =Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 α))[ e^(−(2n+1)αx) ]_0 ^1 =(1/α) Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 )){ e^(−(2n+1)α) −1} = (1/α) Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 )) e^(−(2n+1)α) +(1/α) Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ...be continued...](Q38089.png)
$${we}\:{have}\:{artan}^{'} \left({u}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{u}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$${arctan}\left({u}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{u}^{\mathrm{2}{n}+\mathrm{1}} \:+{c}\:\:\left({c}=\mathrm{0}\right)\Rightarrow \\ $$$${arctan}\left({e}^{−\alpha{x}} \right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}} \:\:{and} \\ $$$${f}\left(\alpha\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({e}^{−\alpha{x}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \alpha}\left[\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\alpha}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\left\{\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:−\mathrm{1}\right\} \\ $$$$=\:\frac{\mathrm{1}}{\alpha}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha} \:\:\:+\frac{\mathrm{1}}{\alpha}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$...{be}\:{continued}... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18
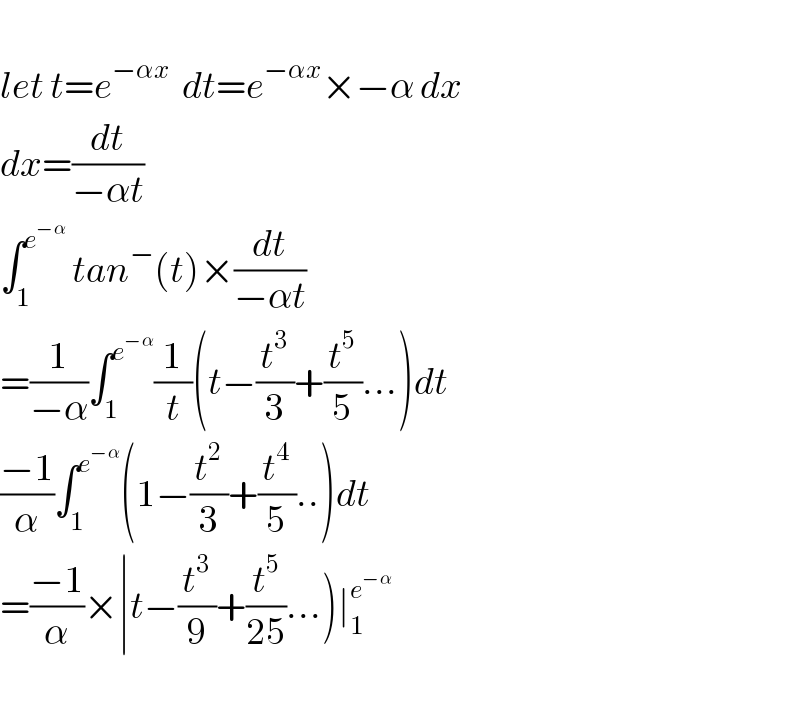
$$ \\ $$$${let}\:{t}={e}^{−\alpha{x}\:\:\:} {dt}={e}^{−\alpha{x}} ×−\alpha\:{dx} \\ $$$${dx}=\frac{{dt}}{−\alpha{t}} \\ $$$$\int_{\mathrm{1}} ^{{e}^{−\alpha} } \:{tan}^{−} \left({t}\right)×\frac{{dt}}{−\alpha{t}} \\ $$$$=\frac{\mathrm{1}}{−\alpha}\int_{\mathrm{1}} ^{{e}^{−\alpha} } \frac{\mathrm{1}}{{t}}\left({t}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+\frac{{t}^{\mathrm{5}} }{\mathrm{5}}...\right){dt} \\ $$$$\frac{−\mathrm{1}}{\alpha}\int_{\mathrm{1}} ^{{e}^{−\alpha} } \left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{3}}+\frac{{t}^{\mathrm{4}} }{\mathrm{5}}..\right){dt} \\ $$$$\left.=\frac{−\mathrm{1}}{\alpha}×\mid{t}−\frac{{t}^{\mathrm{3}} }{\mathrm{9}}+\frac{{t}^{\mathrm{5}} }{\mathrm{25}}...\right)\mid_{\mathrm{1}} ^{{e}^{−\alpha} } \\ $$$$ \\ $$
