
Question and Answers Forum
Question Number 37912 by gunawan last updated on 19/Jun/18

Commented by math khazana by abdo last updated on 19/Jun/18
![I = ∫_(−(π/2)) ^(π/2) A(θ)sin^2 θdθ with A(θ) = ∫_0 ^(3cosθ) r^2 dr =(1/3)[r^3 ]_0 ^(3cosθ) =(1/3) 27 cos^3 θ =9 cos^3 θ ⇒I =9∫_(−(π/2)) ^(π/2) sin^2 θ cos^3 θ dθ =_(sinθ =t) ∫_(−1) ^1 t^2 (1−t^2 )(√(1−t^2 )) (dt/(√(1−t^2 ))) =∫_(−1) ^1 (t^2 −t^4 )dt=2[ (t^3 /3) −(t^5 /5)]_0 ^1 =2 { (1/3) −(1/5)}=2(2/(15)) =(4/(15)) ⇒ I =9 .(4/(15)) = ((12)/5) I =((12)/5) .](Q37927.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jun/18
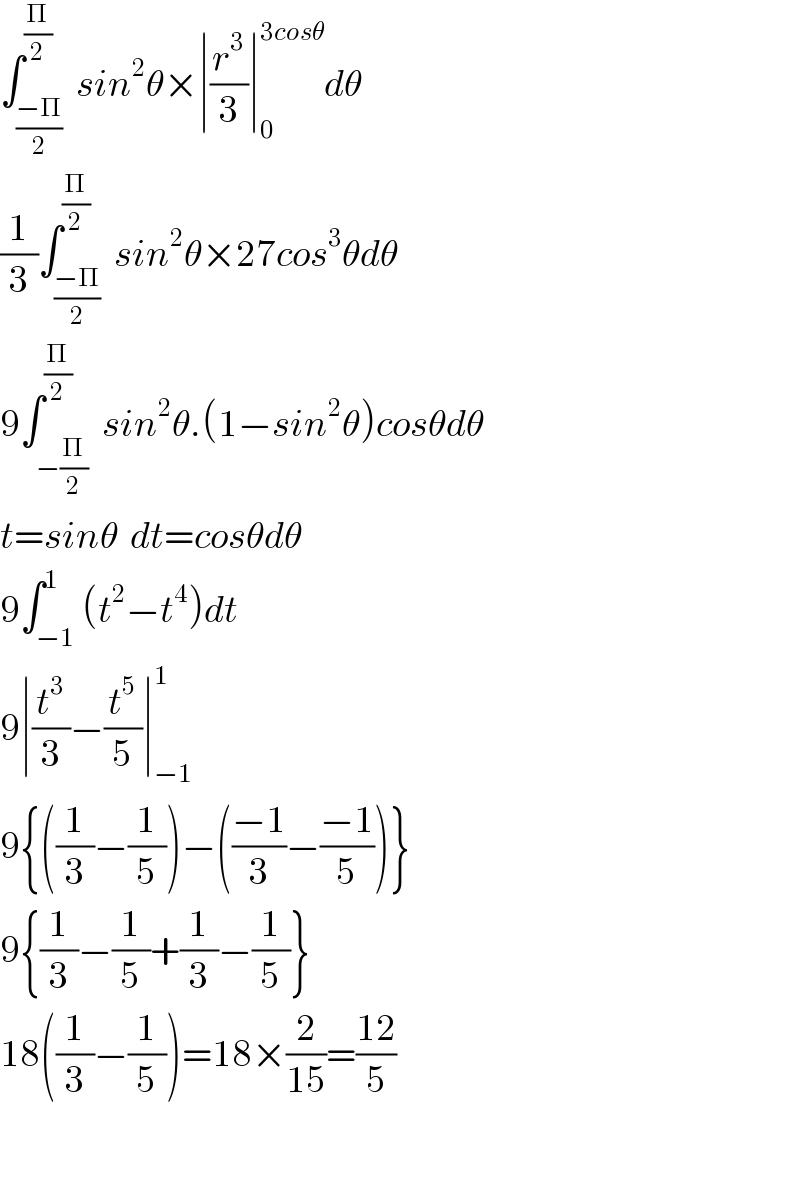
| ||
Question and Answers Forum | ||
Question Number 37912 by gunawan last updated on 19/Jun/18 | ||
 | ||
Commented by math khazana by abdo last updated on 19/Jun/18 | ||
![I = ∫_(−(π/2)) ^(π/2) A(θ)sin^2 θdθ with A(θ) = ∫_0 ^(3cosθ) r^2 dr =(1/3)[r^3 ]_0 ^(3cosθ) =(1/3) 27 cos^3 θ =9 cos^3 θ ⇒I =9∫_(−(π/2)) ^(π/2) sin^2 θ cos^3 θ dθ =_(sinθ =t) ∫_(−1) ^1 t^2 (1−t^2 )(√(1−t^2 )) (dt/(√(1−t^2 ))) =∫_(−1) ^1 (t^2 −t^4 )dt=2[ (t^3 /3) −(t^5 /5)]_0 ^1 =2 { (1/3) −(1/5)}=2(2/(15)) =(4/(15)) ⇒ I =9 .(4/(15)) = ((12)/5) I =((12)/5) .](Q37927.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jun/18 | ||
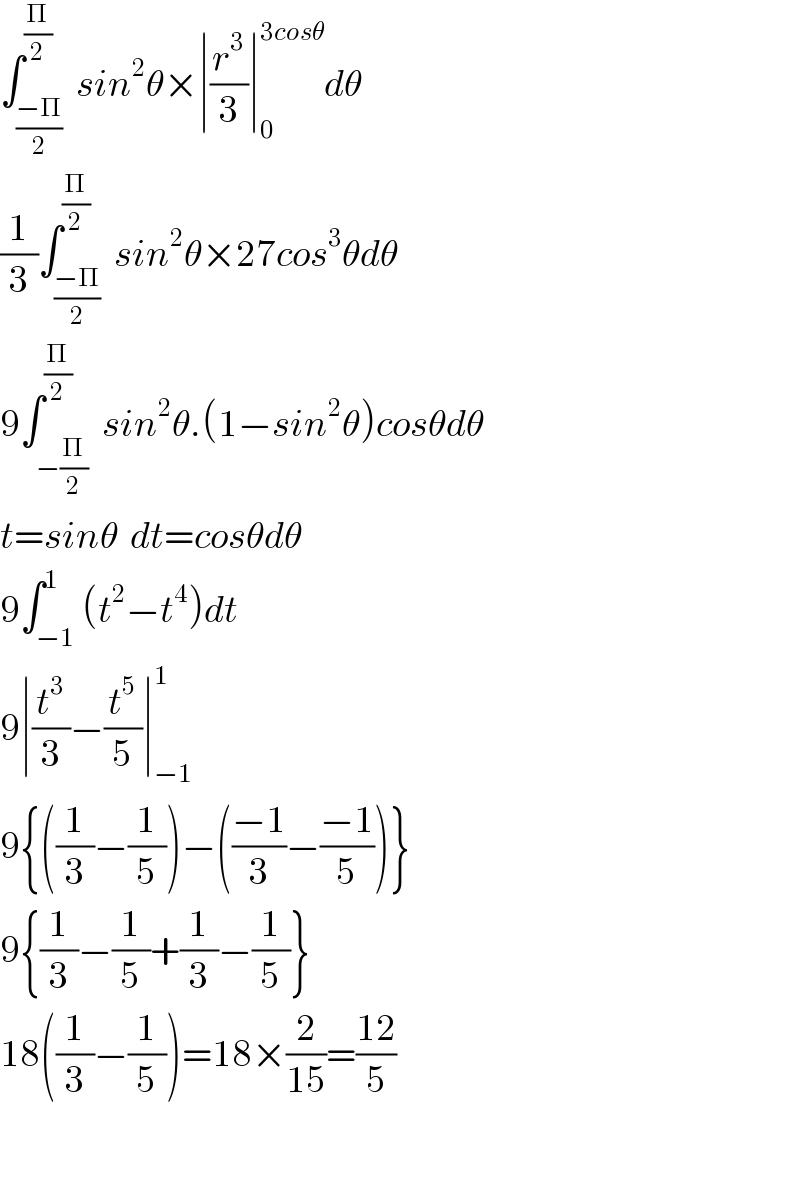 | ||
| ||