
Question and Answers Forum
Question Number 37989 by ajfour last updated on 20/Jun/18

Commented by ajfour last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18
![(i) side length of blue square: a_1 =(a/(cos θ))−a sin θ (1+tan θ) ⇒a_1 =a (cos θ−sin θ) ⇒A_1 =a_1 ^2 =a^2 (1−sin 2θ) side length of red square: a_2 =a tan θ sin α with tan α=(a/(a−a tan θ))=((cos θ)/(cos θ−sin θ)) or sin α=((cos θ)/(√(1+cos^2 θ−sin 2θ))) ⇒a_2 =a ((sin θ)/(√(1+cos^2 θ−sin 2θ))) ⇒A_2 =a_2 ^2 =a^2 ((sin^2 θ)/(1+cos^2 θ−sin 2θ)) (ii) a_1 =a_2 [sin (α−θ)+cos (α−θ)] a_1 =a_2 [sin α (sin θ+cos θ)+cos α (cos θ−sin θ)] (cos θ−sin θ)=((sin θ)/(√(1+cos^2 θ−sin 2θ)))[((cos θ (sin θ+cos θ))/(√(1+cos^2 θ−sin 2θ))) +(((cos θ−sin θ)^2 )/(√(1+cos^2 θ−sin 2θ)))] cos θ−sin θ=((sin θ (sin θ cos θ+cos^2 θ+1−sin 2θ))/(1+cos^2 θ−sin 2θ)) cos θ−sin θ=((sin^2 θ cos θ)/(1+cos^2 θ−sin 2θ))+sin θ 2(cos θ−2sin θ)=((sin θ sin 2θ)/(1+cos^2 θ−sin 2θ)) 2(cos θ−2sin θ)(1+cos^2 θ+sin 2θ)=sin θ sin 2θ ⇒θ≈23.3°](Q37993.png)
Commented by ajfour last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18
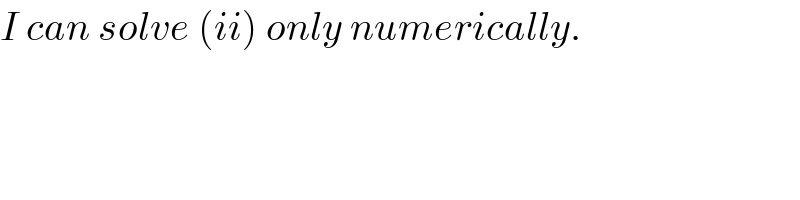
Commented by ajfour last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18

Answered by ajfour last updated on 20/Jun/18
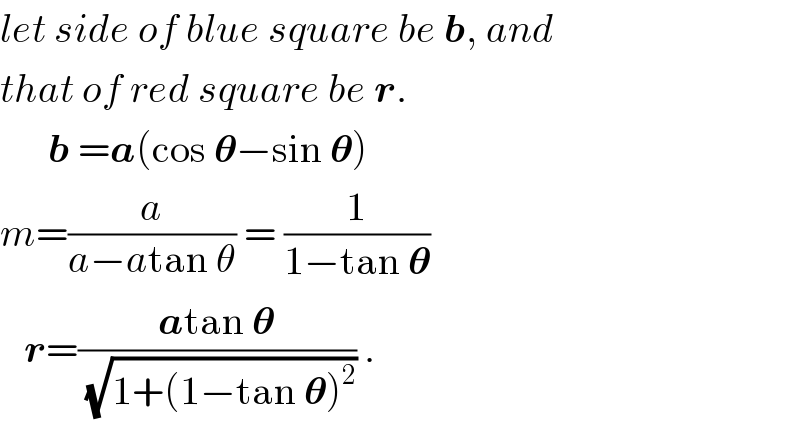
Answered by ajfour last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18
��
