Question Number 38058 by ajfour last updated on 21/Jun/18
$$\int\frac{\mathrm{tan}\:{x}}{{a}+{b}\mathrm{tan}\:^{\mathrm{2}} {x}}\:{dx}\:\:=\:? \\ $$
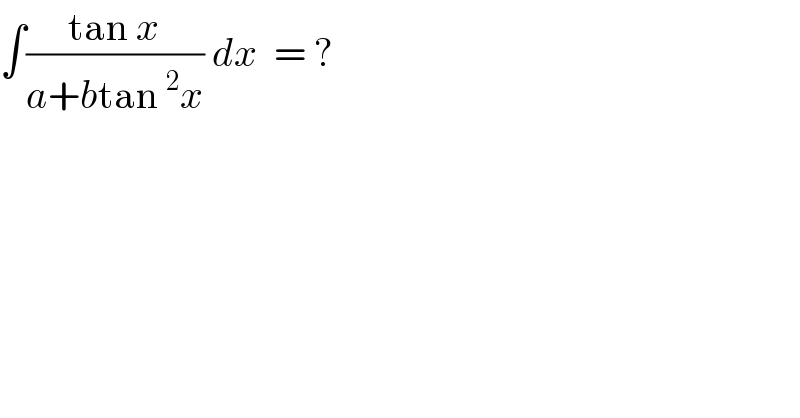
Answered by behi83417@gmail.com last updated on 21/Jun/18
![tg^2 x=(a/b)t⇒2tgx(1+tg^2 x)dx=(a/b)dt 2tgxdx=(((a/b)dt)/(1+(a/b)t))⇒tgxdx=((adt)/(2(b+at))) I=∫(((adt)/(2(b+at)))/(a+at))=(1/2)∫(dt/((1+t)(b+at)))= (1/(2(b−a)))∫[(1/(1+t))−(a/(b+at))]dt= =(1/(2(b−a)))[ln(1+t)−ln(b+at)+const]= =(1/(2(b−a)))[ln(1+(b/a)tg^2 x)−ln(b+btg^2 x)+c]= =(1/(2(b−a)))ln(a.cos^2 x+b.sin^2 x)+const. ■ (1/((1+t)(b+at)))=(A/(1+t))+(B/(b+at)) t=−1⇒(1/(b−a))=A,t=0⇒B=1−(b/(b−a))=(a/(a−b))](Q38064.png)
$${tg}^{\mathrm{2}} {x}=\frac{{a}}{{b}}{t}\Rightarrow\mathrm{2}{tgx}\left(\mathrm{1}+{tg}^{\mathrm{2}} {x}\right){dx}=\frac{{a}}{{b}}{dt} \\ $$$$\mathrm{2}{tgxdx}=\frac{\frac{{a}}{{b}}{dt}}{\mathrm{1}+\frac{{a}}{{b}}{t}}\Rightarrow{tgxdx}=\frac{{adt}}{\mathrm{2}\left({b}+{at}\right)} \\ $$$${I}=\int\frac{\frac{{adt}}{\mathrm{2}\left({b}+{at}\right)}}{{a}+{at}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left(\mathrm{1}+{t}\right)\left({b}+{at}\right)}=\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}\int\left[\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{{a}}{{b}+{at}}\right]{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}\left[{ln}\left(\mathrm{1}+{t}\right)−{ln}\left({b}+{at}\right)+{const}\right]= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}\left[\boldsymbol{{ln}}\left(\mathrm{1}+\frac{\boldsymbol{{b}}}{\boldsymbol{{a}}}\boldsymbol{{tg}}^{\mathrm{2}} \boldsymbol{{x}}\right)−\boldsymbol{{ln}}\left(\boldsymbol{{b}}+\boldsymbol{{btg}}^{\mathrm{2}} \boldsymbol{{x}}\right)+\boldsymbol{{c}}\right]= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\boldsymbol{{b}}−\boldsymbol{{a}}\right)}\boldsymbol{{ln}}\left(\boldsymbol{{a}}.\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{b}}.\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right)+\boldsymbol{{const}}.\:\blacksquare \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)\left({b}+{at}\right)}=\frac{{A}}{\mathrm{1}+{t}}+\frac{{B}}{{b}+{at}} \\ $$$${t}=−\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{b}−{a}}={A},{t}=\mathrm{0}\Rightarrow{B}=\mathrm{1}−\frac{{b}}{{b}−{a}}=\frac{{a}}{{a}−{b}} \\ $$
Commented by ajfour last updated on 21/Jun/18
$${thank}\:{you}\:{sir}. \\ $$
Answered by ajfour last updated on 21/Jun/18
$${I}=\int\frac{\mathrm{sin}\:{x}\mathrm{cos}\:{x}}{{a}\mathrm{cos}\:^{\mathrm{2}} {x}+{b}\mathrm{sin}\:^{\mathrm{2}} {x}}{dx} \\ $$$${d}\left({a}\mathrm{cos}\:^{\mathrm{2}} {x}+{b}\mathrm{sin}\:^{\mathrm{2}} {x}\right)= \\ $$$$\:\:\:\:\:\:\left({b}−{a}\right)\mathrm{sin}\:\mathrm{2}{xdx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}\mathrm{ln}\:\mid{a}\mathrm{cos}\:^{\mathrm{2}} {x}+{b}\mathrm{sin}\:^{\mathrm{2}} {x}\mid+{c}\:. \\ $$
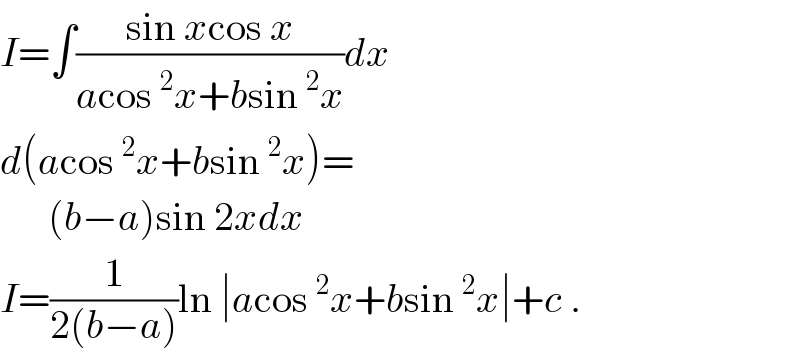
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18
$${tricky}...{bah}...{darun}.. \\ $$$$ \\ $$
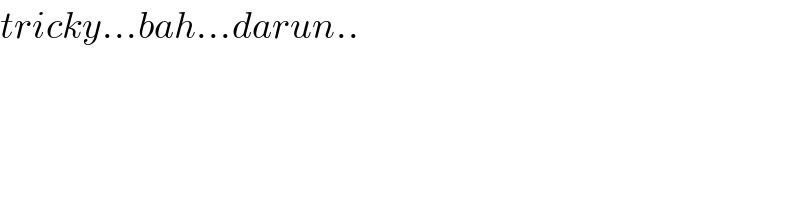
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18
$$\int\frac{{tanx}.{cos}^{\mathrm{2}} {x}}{{acos}^{\mathrm{2}} {x}+{bsin}^{\mathrm{2}} {x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{sinxcosx}}{{acos}^{\mathrm{2}} {x}+{bsin}^{\mathrm{2}} {x}}{dx} \\ $$$${t}={acos}^{\mathrm{2}} {x}+{bsin}^{\mathrm{2}} {x} \\ $$$${dt}=\left({a}×−{sin}\mathrm{2}{x}+{b}×{sin}\mathrm{2}{x}\right){dx} \\ $$$${dt}=\left({b}−{a}\right){sin}\mathrm{2}{xdx} \\ $$$$\frac{{dt}}{{b}−{a}}={sin}\mathrm{2}{xdx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{{b}−{a}}\int\frac{{dt}}{{t}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}{lnt}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left({b}−{a}\right)}{ln}\left({acos}^{\mathrm{2}} {x}+{bsin}^{\mathrm{2}} {x}\right)+{c} \\ $$$${so}\:{intregatin}\:{is}\:{independent}\:{of}\:{power}\:{a} \\ $$$${whether}\:{a}\:{or}\:{a}^{\mathrm{2}} \\ $$