∫(dx/(a+btan^2 x)) = ?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 38074 by ajfour last updated on 21/Jun/18

$\int \frac{d x}{a + b \tan^{2} x} = ?$
Commented by prof Abdo imad last updated on 21/Jun/18
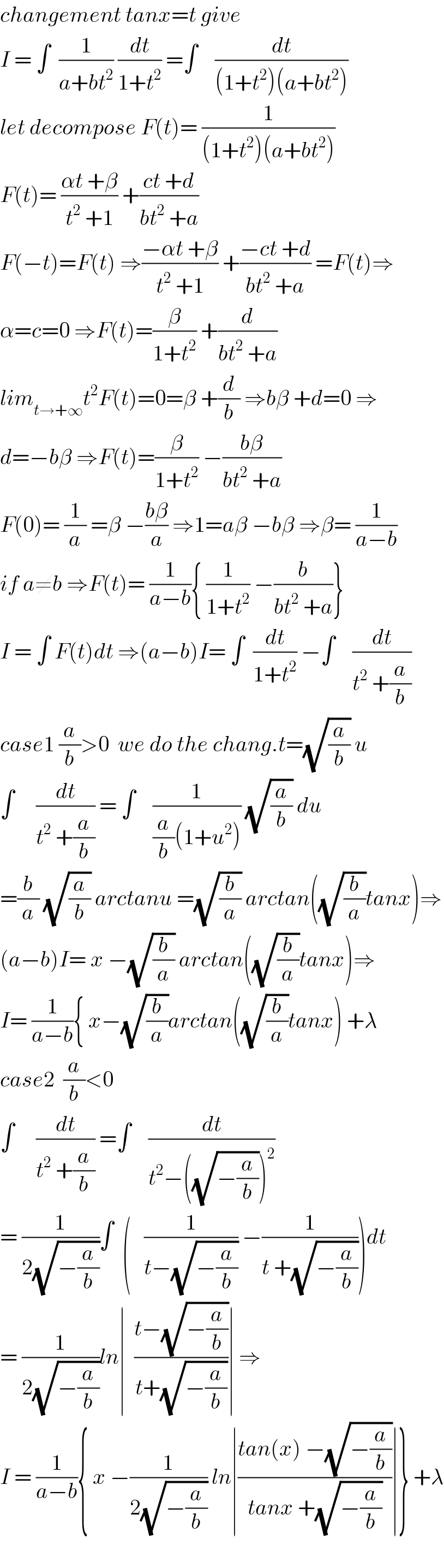
$changement tanx=t give I = ∫ (1/(a+bt^2 )) (dt/(1+t^2 )) =∫ (dt/((1+t^2 )(a+bt^2 ))) let decompose F(t)= (1/((1+t^2 )(a+bt^2 ))) F(t)= ((αt +β)/(t^2 +1)) +((ct +d)/(bt^2 +a)) F(−t)=F(t) ⇒((−αt +β)/(t^2 +1)) +((−ct +d)/(bt^2 +a)) =F(t)⇒ α=c=0 ⇒F(t)=(β/(1+t^2 )) +(d/(bt^2 +a)) lim_(t→+∞) t^2 F(t)=0=β +(d/b) ⇒bβ +d=0 ⇒ d=−bβ ⇒F(t)=(β/(1+t^2 )) −((bβ)/(bt^2 +a)) F(0)= (1/a) =β −((bβ)/a) ⇒1=aβ −bβ ⇒β= (1/(a−b)) if a≠b ⇒F(t)= (1/(a−b)){ (1/(1+t^2 )) −(b/(bt^2 +a))} I = ∫ F(t)dt ⇒(a−b)I= ∫ (dt/(1+t^2 )) −∫ (dt/(t^2 +(a/b))) case1 (a/b)>0 we do the chang.t=(√(a/b)) u ∫ (dt/(t^2 +(a/b))) = ∫ (1/((a/b)(1+u^2 ))) (√(a/b)) du =(b/a) (√(a/b)) arctanu =(√(b/a)) arctan((√(b/a))tanx)⇒ (a−b)I= x −(√(b/a)) arctan((√(b/a))tanx)⇒ I= (1/(a−b)){ x−(√(b/a))arctan((√(b/a))tanx) +λ case2 (a/b)<0 ∫ (dt/(t^2 +(a/b))) =∫ (dt/(t^2 −((√(−(a/b))))^2 )) = (1/(2(√(−(a/b)))))∫ ( (1/(t−(√(−(a/b))))) −(1/(t +(√(−(a/b))))))dt = (1/(2(√(−(a/b)))))ln∣ ((t−(√(−(a/b))))/(t+(√(−(a/b)))))∣ ⇒ I = (1/(a−b)){ x −(1/(2(√(−(a/b))))) ln∣((tan(x) −(√(−(a/b))))/(tanx +(√(−(a/b)))))∣} +λ$
$c h a n g e m e n t t a n x = t g i v e$ $I = \int \frac{1}{a + {b t}^{2}} \frac{d t}{1 + t^{2}} = \int \frac{d t}{(1 + t^{2}) (a + {b t}^{2})}$ $l e t d e c o m p o s e F (t) = \frac{1}{(1 + t^{2}) (a + {b t}^{2})}$ $F (t) = \frac{α t + β}{t^{2} + 1} + \frac{c t + d}{{b t}^{2} + a}$ $F (- t) = F (t) \Rightarrow \frac{- α t + β}{t^{2} + 1} + \frac{- c t + d}{{b t}^{2} + a} = F (t) \Rightarrow$ $α = c = 0 \Rightarrow F (t) = \frac{β}{1 + t^{2}} + \frac{d}{{b t}^{2} + a}$ ${l i m}_{t \to + \infty} t^{2} F (t) = 0 = β + \frac{d}{b} \Rightarrow b β + d = 0 \Rightarrow$ $d = - b β \Rightarrow F (t) = \frac{β}{1 + t^{2}} - \frac{b β}{{b t}^{2} + a}$ $F (0) = \frac{1}{a} = β - \frac{b β}{a} \Rightarrow 1 = a β - b β \Rightarrow β = \frac{1}{a - b}$ $i f a \neq b \Rightarrow F (t) = \frac{1}{a - b} {\frac{1}{1 + t^{2}} - \frac{b}{{b t}^{2} + a}}$ $I = \int F (t) d t \Rightarrow (a - b) I = \int \frac{d t}{1 + t^{2}} - \int \frac{d t}{t^{2} + \frac{a}{b}}$ $c a s e 1 \frac{a}{b} > 0 w e d o t h e c h a n g . t = \sqrt{\frac{a}{b}} u$ $\int \frac{d t}{t^{2} + \frac{a}{b}} = \int \frac{1}{\frac{a}{b} (1 + u^{2})} \sqrt{\frac{a}{b}} d u$ $= \frac{b}{a} \sqrt{\frac{a}{b}} a r c t a n u = \sqrt{\frac{b}{a}} a r c t a n (\sqrt{\frac{b}{a}} t a n x) \Rightarrow$ $(a - b) I = x - \sqrt{\frac{b}{a}} a r c t a n (\sqrt{\frac{b}{a}} t a n x) \Rightarrow$ $I = \frac{1}{a - b} {x - \sqrt{\frac{b}{a}} a r c t a n (\sqrt{\frac{b}{a}} t a n x) + λ$ $c a s e 2 \frac{a}{b} < 0$ $\int \frac{d t}{t^{2} + \frac{a}{b}} = \int \frac{d t}{t^{2} - {(\sqrt{- \frac{a}{b}})}^{2}}$ $= \frac{1}{2 \sqrt{- \frac{a}{b}}} \int (\frac{1}{t - \sqrt{- \frac{a}{b}}} - \frac{1}{t + \sqrt{- \frac{a}{b}}}) d t$ $= \frac{1}{2 \sqrt{- \frac{a}{b}}} l n ∣ \frac{t - \sqrt{- \frac{a}{b}}}{t + \sqrt{- \frac{a}{b}}} ∣ \Rightarrow$ $I = \frac{1}{a - b} {x - \frac{1}{2 \sqrt{- \frac{a}{b}}} l n ∣ \frac{t a n (x) - \sqrt{- \frac{a}{b}}}{t a n x + \sqrt{- \frac{a}{b}}} ∣} + λ$
Commented by prof Abdo imad last updated on 21/Jun/18

$i f a = b I = \frac{1}{a} \int \frac{d x}{1 + {t a n}^{2} x} (a \neq 0)$ $= \frac{1}{a} \int {c o s}^{2} x d x = \frac{1}{a} \int \frac{1 + c o s (2 x)}{2} d x$ $= \frac{x}{2 a} + \frac{1}{4 a} s i n (2 x) + λ .$
Commented by ajfour last updated on 21/Jun/18

$W o w S i r, t h a n k y o u .$
Commented by math khazana by abdo last updated on 21/Jun/18

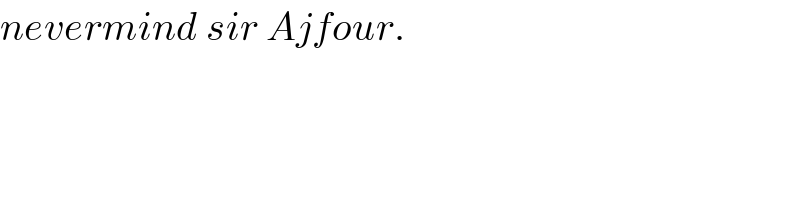
$n e v e r m i n d s i r A j f o u r .$
	Answered by behi83417@gmail.com last updated on 21/Jun/18

	${t g}^{2} x = \frac{a}{b} t \Rightarrow t g x = \sqrt{\frac{a}{b} t}$ $2 t g x (1 + {t g}^{2} x) d x = \frac{a}{b} d t \Rightarrow$ $2 \sqrt{\frac{a t}{b}} (1 + \frac{a t}{b}) d x = \frac{a}{b} d t \Rightarrow d x = \frac{a d t}{2 \sqrt{\frac{a t}{b}} . (b + a t)}$ $\Rightarrow I = \frac{1}{2 \sqrt{\frac{a}{b}}} \int \frac{\frac{a d t}{\sqrt{t} (b + a t)}}{a + a t} = m \int \frac{d t}{\sqrt{t} (1 + t) (b + a t)}$ $m = {(2 \sqrt{\frac{a}{b}})}^{- 1}, t = u^{2} \Rightarrow d t = 2 u d u$ $I = m \int \frac{2 u d u}{u (1 + u^{2}) (b + {a u}^{2})} = 2 m \int \frac{d u}{(1 + u^{2}) (b + {a u}^{2})} =$ $= 2 m [a . \frac{1}{4 \sqrt{a b}} {t g}^{- 1} (a . \frac{u}{\sqrt{a b}}) - \frac{1}{4} {t g}^{- 1} u] + c o n s t$ $= \frac{1}{2} m [\sqrt{\frac{a}{b}} . {t g}^{- 1} (\sqrt{\frac{a}{b}} u) - {t g}^{- 1} u + c o n s t =$ $= \frac{1}{2} . \frac{1}{2} \sqrt{\frac{b}{a}} . \sqrt{\frac{a}{b}} {t g}^{- 1} (\sqrt{\frac{a}{b}} . \sqrt{\frac{b}{a}} . t g x) -$ $- \frac{1}{4} . \sqrt{\frac{b}{a}} . {t g}^{- 1} (\sqrt{\frac{b}{a}} . t g x) + c o n s t =$ $= \frac{1}{4} x - \frac{1}{4} . \sqrt{\frac{b}{a}} . a r c t g [\sqrt{\frac{b}{a}} . t g x] + c o n s t . ◼$
	Commented by ajfour last updated on 21/Jun/18

	$G o d b l e s s y o u S i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum