Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 3808 by Rasheed Soomro last updated on 21/Dec/15

A chord divides the circle in two segments,having areas s_1 and s_2 . If diameter, perpendicular to this chord is cut into 1:3 by the chord ,what is s_1 :s_2 ?

$${A}\:{chord}\:{divides}\:\:{the}\:{circle}\:{in}\:{two} \\ $$$${segments},{having}\:{areas}\:{s}_{\mathrm{1}} \:{and}\:\:{s}_{\mathrm{2}} . \\ $$$${If}\:{diameter},\:{perpendicular}\:{to}\:{this} \\ $$$${chord}\:{is}\:{cut}\:{into}\:\mathrm{1}:\mathrm{3}\:{by}\:{the}\:{chord}\:,{what}\:{is}\:{s}_{\mathrm{1}} :{s}_{\mathrm{2}} \:? \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 21/Dec/15

Let AB is a chord and CD (⊥AB) is a diameter. Let AB cuts CD at point O If CO:OD=1:3 , what is s_1 :s_2 s_1 and s_2 are areas of two segments of the circle produced by chord AB.

$${Let}\:{AB}\:{is}\:{a}\:{chord}\:{and}\:{CD}\:\left(\bot{AB}\right)\:{is}\:\:{a}\:{diameter}. \\ $$$${Let}\:{AB}\:{cuts}\:{CD}\:{at}\:{point}\:{O} \\ $$$${If}\:{CO}:{OD}=\mathrm{1}:\mathrm{3}\:,\:{what}\:{is}\:{s}_{\mathrm{1}} :{s}_{\mathrm{2}} \\ $$$${s}_{\mathrm{1}} \:{and}\:{s}_{\mathrm{2}} \:{are}\:{areas}\:{of}\:{two}\:{segments}\:{of}\:{the} \\ $$$${circle}\:{produced}\:{by}\:{chord}\:{AB}. \\ $$

Answered by Yozzii last updated on 21/Dec/15

(Integral Calculus can alternatively be used to find the value of (s_1 /s_2 ).) Draw a circle with diameter length d and centre Q. A diameter of the circle normally cuts a chord AB on the circle such that d is partitioned in the ratio 1:3. Let LF be such a diameter and D be the point of intersection of the chord AB and diameter LF. We thus have ∣LD∣=3a and ∣DF∣=a (a>0) so that DF:LD=1:3. Therefore, d=3a+a=4a⇒ radius r=2a. Complete the isosceles triangle △AQB and let ∠AQB=θ. The area A_(1 ) of the sector AB of the circle is then A_1 =(1/2)r^2 θ=(1/2)×4a^2 θ=2a^2 θ. The area of △AQB,denoted by A_2 , is given by A_2 =(1/2)2a×2a×sinθ=2a^2 sinθ. Now, let s_1 be the area between the chord AB and the arc AB. ⇒s_1 =A_1 −A_2 =2a^2 (θ−sinθ) Hence, the area of the other segment of the circle is s_2 =πr^2 −s_1 . s_2 =4πa^2 −2a^2 (θ−sinθ) s_2 =2a^2 (2π+sinθ−θ) Therefore, (s_1 /s_2 )=((θ−sinθ)/(2π+sinθ−θ)). Returning to △AQB, we can yield a right−angled triangle △AQD with ∠AQD=(1/2)∠AQB=(θ/2) and ∠QDA=(π/2). We then have cos(θ/2)=((QD)/(AQ))=(a/(2a))=(1/2) ⇒(θ/2)=(π/3)⇒θ=((2π)/3). ∴ (s_1 /s_2 )=((((2π)/3)−sin((2π)/3))/(2π+sin((2π)/3)−((2π)/3)))=((((2π)/3)−((√3)/2))/(2π+((√3)/2)−((2π)/3))) (s_1 /s_2 )=((4π−3(√3))/(8π+3(√3)))

$$\left({Integral}\:{Calculus}\:{can}\:{alternatively}\right. \\ $$$$\left.{be}\:{used}\:{to}\:{find}\:{the}\:{value}\:{of}\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }.\right) \\ $$$${Draw}\:{a}\:{circle}\:{with}\:{diameter}\:{length}\:{d}\:{and}\: \\ $$$${centre}\:{Q}.\:{A}\:{diameter}\:{of}\:{the}\:{circle}\:{normally} \\ $$$${cuts}\:{a}\:{chord}\:{AB}\:{on}\:{the}\:{circle}\:{such}\:{that} \\ $$$${d}\:{is}\:{partitioned}\:{in}\:{the}\:{ratio}\:\mathrm{1}:\mathrm{3}.\:{Let} \\ $$$${LF}\:\:{be}\:{such}\:{a}\:{diameter}\:{and}\:{D}\:{be}\:{the}\: \\ $$$${point}\:{of}\:{intersection}\:{of}\:{the}\:{chord}\:{AB} \\ $$$${and}\:{diameter}\:{LF}.\:{We}\:{thus}\:{have}\: \\ $$$$\mid{LD}\mid=\mathrm{3}{a}\:{and}\:\mid{DF}\mid={a}\:\left({a}>\mathrm{0}\right)\:{so}\:{that}\:{DF}:{LD}=\mathrm{1}:\mathrm{3}. \\ $$$${Therefore},\:{d}=\mathrm{3}{a}+{a}=\mathrm{4}{a}\Rightarrow\:{radius}\:{r}=\mathrm{2}{a}. \\ $$$${Complete}\:{the}\:{isosceles}\:{triangle}\:\bigtriangleup{AQB} \\ $$$${and}\:{let}\:\angle{AQB}=\theta.\:{The}\:{area}\:{A}_{\mathrm{1}\:} {of}\:{the}\:{sector}\:{AB} \\ $$$${of}\:{the}\:{circle}\:{is}\:{then} \\ $$$$\:{A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}{a}^{\mathrm{2}} \theta=\mathrm{2}{a}^{\mathrm{2}} \theta. \\ $$$${The}\:{area}\:{of}\:\bigtriangleup{AQB},{denoted}\:{by}\:{A}_{\mathrm{2}} ,\:{is}\:{given}\:{by} \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{a}×\mathrm{2}{a}×{sin}\theta=\mathrm{2}{a}^{\mathrm{2}} {sin}\theta. \\ $$$${Now},\:{let}\:{s}_{\mathrm{1}} \:{be}\:{the}\:{area}\:{between}\:{the}\:{chord} \\ $$$${AB}\:{and}\:{the}\:{arc}\:{AB}.\: \\ $$$$\Rightarrow{s}_{\mathrm{1}} ={A}_{\mathrm{1}} −{A}_{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} \left(\theta−{sin}\theta\right) \\ $$$${Hence},\:{the}\:{area}\:{of}\:{the}\:{other}\:{segment} \\ $$$${of}\:{the}\:{circle}\:{is}\:{s}_{\mathrm{2}} =\pi{r}^{\mathrm{2}} −{s}_{\mathrm{1}} . \\ $$$${s}_{\mathrm{2}} =\mathrm{4}\pi{a}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} \left(\theta−{sin}\theta\right) \\ $$$${s}_{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} \left(\mathrm{2}\pi+{sin}\theta−\theta\right) \\ $$$${Therefore},\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }=\frac{\theta−{sin}\theta}{\mathrm{2}\pi+{sin}\theta−\theta}. \\ $$$${Returning}\:{to}\:\bigtriangleup{AQB},\:{we}\:{can}\:{yield} \\ $$$${a}\:{right}−{angled}\:{triangle}\:\bigtriangleup{AQD} \\ $$$${with}\:\angle{AQD}=\frac{\mathrm{1}}{\mathrm{2}}\angle{AQB}=\frac{\theta}{\mathrm{2}} \\ $$$${and}\:\angle{QDA}=\frac{\pi}{\mathrm{2}}. \\ $$$${We}\:{then}\:{have}\:{cos}\frac{\theta}{\mathrm{2}}=\frac{{QD}}{{AQ}}=\frac{{a}}{\mathrm{2}{a}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{3}}\Rightarrow\theta=\frac{\mathrm{2}\pi}{\mathrm{3}}. \\ $$$$\therefore\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }=\frac{\frac{\mathrm{2}\pi}{\mathrm{3}}−{sin}\frac{\mathrm{2}\pi}{\mathrm{3}}}{\mathrm{2}\pi+{sin}\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}}=\frac{\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}\pi+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }=\frac{\mathrm{4}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}\pi+\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 21/Dec/15

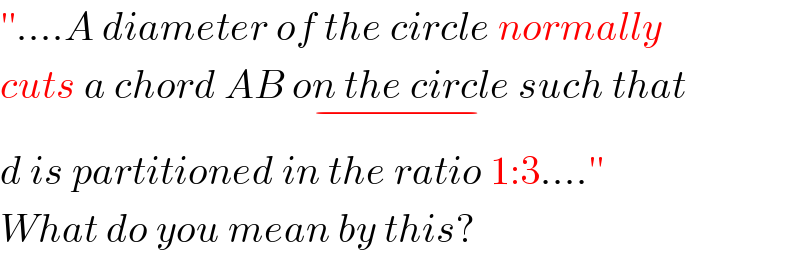
′′....A diameter of the circle normally cuts a chord AB on the circle_(−) such that d is partitioned in the ratio 1:3....′′ What do you mean by this?

$$''....{A}\:{diameter}\:{of}\:{the}\:{circle}\:{normally} \\ $$$${cuts}\:{a}\:{chord}\:{AB}\:\underset{−} {{on}\:{the}\:{circle}}\:{such}\:{that} \\ $$$${d}\:{is}\:{partitioned}\:{in}\:{the}\:{ratio}\:\mathrm{1}:\mathrm{3}....'' \\ $$$${What}\:{do}\:{you}\:{mean}\:{by}\:{this}? \\ $$

Commented by Yozzii last updated on 21/Dec/15

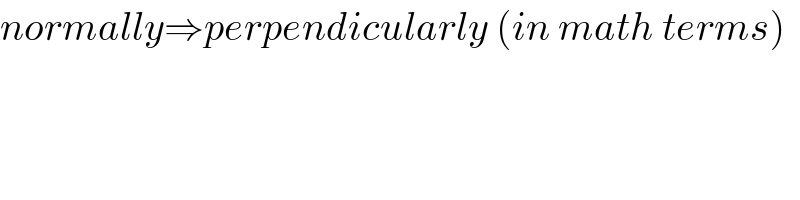
normally⇒perpendicularly (in math terms)

$${normally}\Rightarrow{perpendicularly}\:\left({in}\:{math}\:{terms}\right) \\ $$

Commented by Yozzii last updated on 21/Dec/15

The diameter cuts the chord at 90° with the chord divinding the length of the diameter in the ratio 1:3.

$$ \\ $$$${The}\:{diameter}\:{cuts}\:{the}\:{chord}\:{at}\:\mathrm{90}° \\ $$$${with}\:{the}\:{chord}\:{divinding}\:{the}\:{length}\:{of} \\ $$$${the}\:{diameter}\:{in}\:{the}\:{ratio}\:\mathrm{1}:\mathrm{3}. \\ $$

Commented by Yozzii last updated on 21/Dec/15

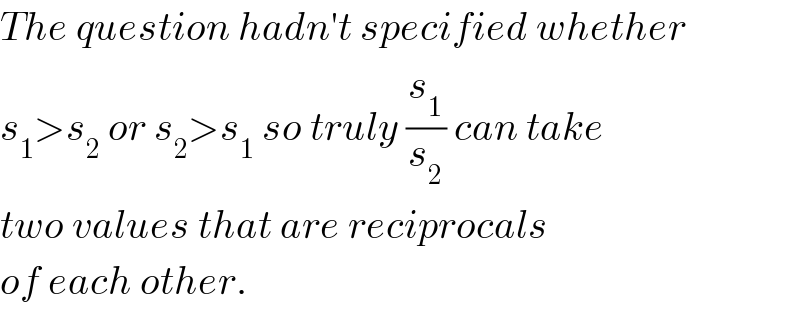
The question hadn′t specified whether s_1 >s_2 or s_2 >s_1 so truly (s_1 /s_2 ) can take two values that are reciprocals of each other.

$${The}\:{question}\:{hadn}'{t}\:{specified}\:{whether} \\ $$$${s}_{\mathrm{1}} >{s}_{\mathrm{2}} \:{or}\:{s}_{\mathrm{2}} >{s}_{\mathrm{1}} \:{so}\:{truly}\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }\:{can}\:{take} \\ $$$${two}\:{values}\:{that}\:{are}\:{reciprocals} \\ $$$${of}\:{each}\:{other}. \\ $$

Commented by Rasheed Soomro last updated on 22/Dec/15

Thanks! Misunderstanding in understanding language.I got ′normally′ in normal language, not as mathematical term.

$${Thanks}!\:{Misunderstanding}\:{in}\:{understanding} \\ $$$${language}.{I}\:{got}\:'\boldsymbol{{normally}}'\:\:{in}\:{normal}\:{language}, \\ $$$${not}\:{as}\:{mathematical}\:{term}. \\ $$

Commented by Rasheed Soomro last updated on 21/Dec/15

G^(O^( V) O) D Approach!

$$\mathcal{G}^{\mathcal{O}^{\:\:{V}} \mathcal{O}} \mathcal{D}\:\mathcal{A}{pproach}! \\ $$

Answered by Yozzii last updated on 21/Dec/15

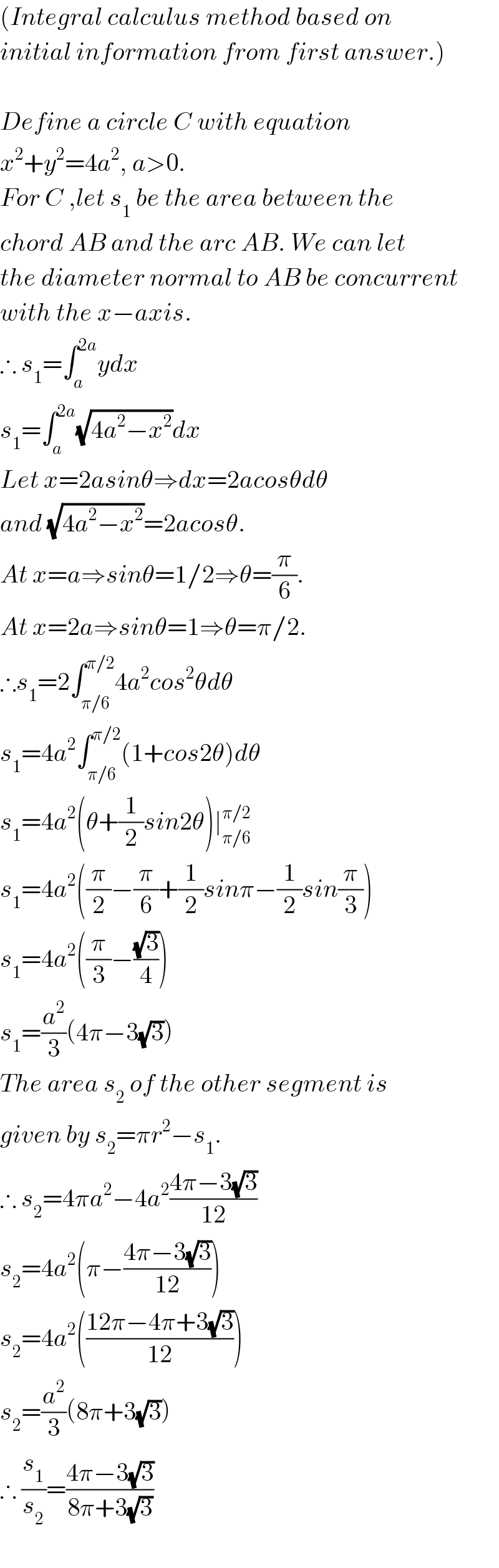
(Integral calculus method based on initial information from first answer.) Define a circle C with equation x^2 +y^2 =4a^2 , a>0. For C ,let s_1 be the area between the chord AB and the arc AB. We can let the diameter normal to AB be concurrent with the x−axis. ∴ s_1 =∫_a ^(2a) ydx s_1 =∫_a ^(2a) (√(4a^2 −x^2 ))dx Let x=2asinθ⇒dx=2acosθdθ and (√(4a^2 −x^2 ))=2acosθ. At x=a⇒sinθ=1/2⇒θ=(π/6). At x=2a⇒sinθ=1⇒θ=π/2. ∴s_1 =2∫_(π/6) ^(π/2) 4a^2 cos^2 θdθ s_1 =4a^2 ∫_(π/6) ^(π/2) (1+cos2θ)dθ s_1 =4a^2 (θ+(1/2)sin2θ)∣_(π/6) ^(π/2) s_1 =4a^2 ((π/2)−(π/6)+(1/2)sinπ−(1/2)sin(π/3)) s_1 =4a^2 ((π/3)−((√3)/4)) s_1 =(a^2 /3)(4π−3(√3)) The area s_2 of the other segment is given by s_2 =πr^2 −s_1 . ∴ s_2 =4πa^2 −4a^2 ((4π−3(√3))/(12)) s_2 =4a^2 (π−((4π−3(√3))/(12))) s_2 =4a^2 (((12π−4π+3(√3))/(12))) s_2 =(a^2 /3)(8π+3(√3)) ∴ (s_1 /s_2 )=((4π−3(√3))/(8π+3(√3)))

$$\left({Integral}\:{calculus}\:{method}\:{based}\:{on}\right. \\ $$$$\left.{initial}\:{information}\:{from}\:{first}\:{answer}.\right) \\ $$$$ \\ $$$${Define}\:{a}\:{circle}\:{C}\:{with}\:{equation}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} ,\:{a}>\mathrm{0}. \\ $$$${For}\:{C}\:,{let}\:{s}_{\mathrm{1}} \:{be}\:{the}\:{area}\:{between}\:{the}\: \\ $$$${chord}\:{AB}\:{and}\:{the}\:{arc}\:{AB}.\:{We}\:{can}\:{let} \\ $$$${the}\:{diameter}\:{normal}\:{to}\:{AB}\:{be}\:{concurrent} \\ $$$${with}\:{the}\:{x}−{axis}. \\ $$$$\therefore\:{s}_{\mathrm{1}} =\int_{{a}} ^{\mathrm{2}{a}} {ydx} \\ $$$${s}_{\mathrm{1}} =\int_{{a}} ^{\mathrm{2}{a}} \sqrt{\mathrm{4}{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx} \\ $$$${Let}\:{x}=\mathrm{2}{asin}\theta\Rightarrow{dx}=\mathrm{2}{acos}\theta{d}\theta \\ $$$${and}\:\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{2}{acos}\theta. \\ $$$${At}\:{x}={a}\Rightarrow{sin}\theta=\mathrm{1}/\mathrm{2}\Rightarrow\theta=\frac{\pi}{\mathrm{6}}. \\ $$$${At}\:{x}=\mathrm{2}{a}\Rightarrow{sin}\theta=\mathrm{1}\Rightarrow\theta=\pi/\mathrm{2}. \\ $$$$\therefore{s}_{\mathrm{1}} =\mathrm{2}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{2}} \mathrm{4}{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta{d}\theta \\ $$$${s}_{\mathrm{1}} =\mathrm{4}{a}^{\mathrm{2}} \int_{\pi/\mathrm{6}} ^{\pi/\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{2}\theta\right){d}\theta \\ $$$${s}_{\mathrm{1}} =\mathrm{4}{a}^{\mathrm{2}} \left(\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right)\mid_{\pi/\mathrm{6}} ^{\pi/\mathrm{2}} \\ $$$${s}_{\mathrm{1}} =\mathrm{4}{a}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\pi−\frac{\mathrm{1}}{\mathrm{2}}{sin}\frac{\pi}{\mathrm{3}}\right) \\ $$$${s}_{\mathrm{1}} =\mathrm{4}{a}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$${s}_{\mathrm{1}} =\frac{{a}^{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{4}\pi−\mathrm{3}\sqrt{\mathrm{3}}\right) \\ $$$${The}\:{area}\:{s}_{\mathrm{2}} \:{of}\:{the}\:{other}\:{segment}\:{is}\: \\ $$$${given}\:{by}\:{s}_{\mathrm{2}} =\pi{r}^{\mathrm{2}} −{s}_{\mathrm{1}} . \\ $$$$\therefore\:{s}_{\mathrm{2}} =\mathrm{4}\pi{a}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} \frac{\mathrm{4}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{12}} \\ $$$${s}_{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \left(\pi−\frac{\mathrm{4}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{12}}\right) \\ $$$${s}_{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \left(\frac{\mathrm{12}\pi−\mathrm{4}\pi+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{12}}\right) \\ $$$${s}_{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{8}\pi+\mathrm{3}\sqrt{\mathrm{3}}\right) \\ $$$$\therefore\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }=\frac{\mathrm{4}\pi−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}\pi+\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 21/Dec/15

AnOther G D^( O^( V) O) Approach!

$$\:\mathbb{A}\mathrm{n}\mathbb{O}\boldsymbol{\mathrm{ther}} \\ $$$$\:\:\:\overset{\:\mathcal{O}^{\:\mathbb{V}} \mathcal{O}} {\mathcal{G}\:\:\:\:\:\:\:\:\mathcal{D}}\: \\ $$$$\mathrm{Approach}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com