Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 38094 by ajfour last updated on 21/Jun/18

Commented by ajfour last updated on 21/Jun/18

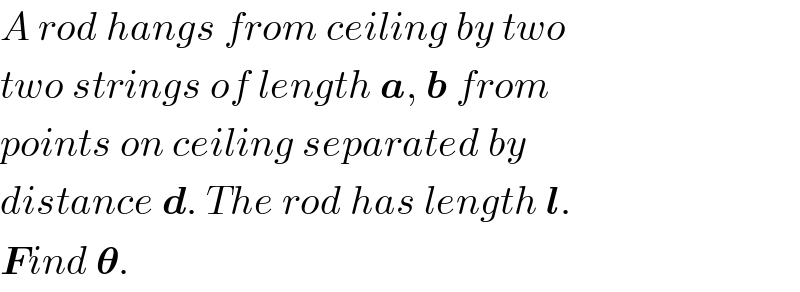
A rod hangs from ceiling by two two strings of length a, b from points on ceiling separated by distance d. The rod has length l. Find 𝛉.

$${A}\:{rod}\:{hangs}\:{from}\:{ceiling}\:{by}\:{two} \\ $$$${two}\:{strings}\:{of}\:{length}\:\boldsymbol{{a}},\:\boldsymbol{{b}}\:{from} \\ $$$${points}\:{on}\:{ceiling}\:{separated}\:{by} \\ $$$${distance}\:\boldsymbol{{d}}.\:{The}\:{rod}\:{has}\:{length}\:\boldsymbol{{l}}. \\ $$$$\boldsymbol{{F}}{ind}\:\boldsymbol{\theta}. \\ $$

Commented by MrW3 last updated on 23/Jun/18

Image that we could extend the strings into the ceiling, then they would meet at a point, let′s say point O. Point O must lie on the same vertical line as the COM of the rod, let′s say point M. So in a first step I would try to solve the easier case where the rod hangs on the point O through two strings with lengthes l_1 and l_2 . We will also have this case if d=0.

$${Image}\:{that}\:{we}\:{could}\:{extend}\:{the}\:{strings} \\ $$$${into}\:{the}\:{ceiling},\:{then}\:{they}\:{would}\:{meet} \\ $$$${at}\:{a}\:{point},\:{let}'{s}\:{say}\:{point}\:{O}. \\ $$$${Point}\:{O}\:{must}\:{lie}\:{on}\:{the}\:{same}\:{vertical} \\ $$$${line}\:{as}\:{the}\:{COM}\:{of}\:{the}\:{rod},\:{let}'{s}\:{say} \\ $$$${point}\:{M}. \\ $$$${So}\:{in}\:{a}\:{first}\:{step}\:{I}\:{would}\:{try}\:{to}\:{solve} \\ $$$${the}\:{easier}\:{case}\:{where}\:{the}\:{rod}\:{hangs}\:{on} \\ $$$${the}\:{point}\:{O}\:{through}\:{two}\:{strings}\:{with} \\ $$$${lengthes}\:{l}_{\mathrm{1}} \:{and}\:{l}_{\mathrm{2}} .\:\:{We}\:{will}\:{also}\:{have} \\ $$$${this}\:{case}\:{if}\:{d}=\mathrm{0}. \\ $$

Commented by MrW3 last updated on 23/Jun/18

Commented by MrW3 last updated on 23/Jun/18

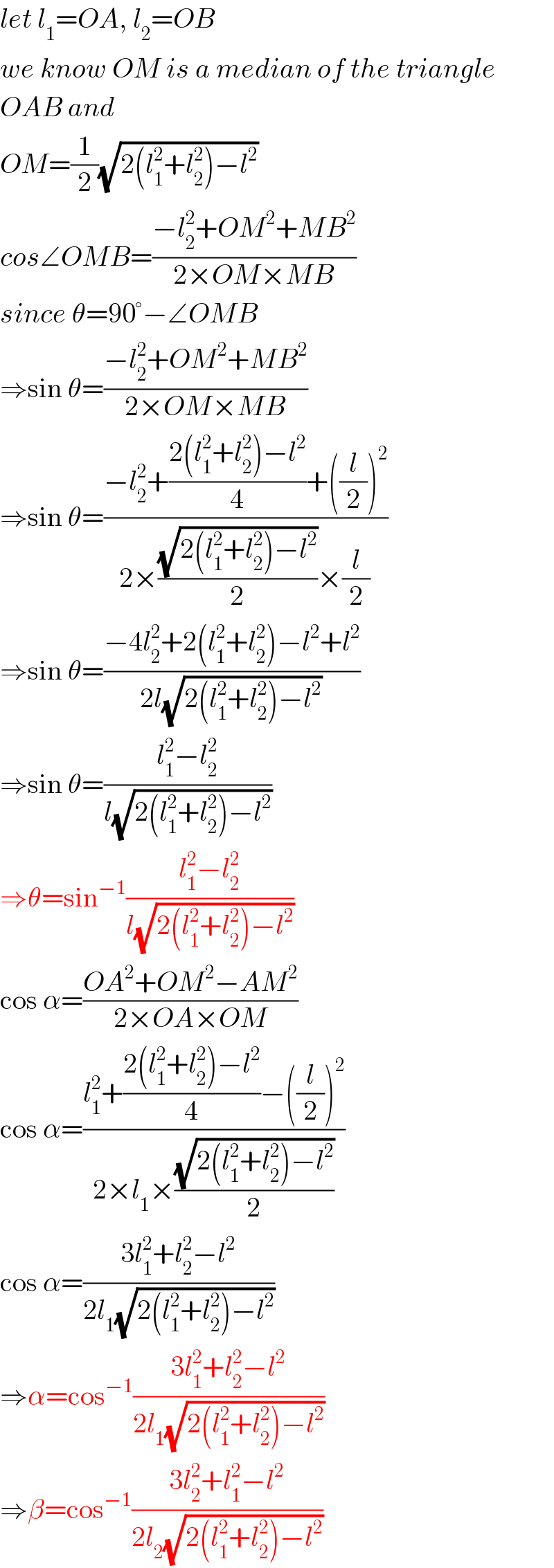
let l_1 =OA, l_2 =OB we know OM is a median of the triangle OAB and OM=(1/2)(√(2(l_1 ^2 +l_2 ^2 )−l^2 )) cos∠OMB=((−l_2 ^2 +OM^2 +MB^2 )/(2×OM×MB)) since θ=90°−∠OMB ⇒sin θ=((−l_2 ^2 +OM^2 +MB^2 )/(2×OM×MB)) ⇒sin θ=((−l_2 ^2 +((2(l_1 ^2 +l_2 ^2 )−l^2 )/4)+((l/2))^2 )/(2×((√(2(l_1 ^2 +l_2 ^2 )−l^2 ))/2)×(l/2))) ⇒sin θ=((−4l_2 ^2 +2(l_1 ^2 +l_2 ^2 )−l^2 +l^2 )/(2l(√(2(l_1 ^2 +l_2 ^2 )−l^2 )))) ⇒sin θ=((l_1 ^2 −l_2 ^2 )/(l(√(2(l_1 ^2 +l_2 ^2 )−l^2 )))) ⇒θ=sin^(−1) ((l_1 ^2 −l_2 ^2 )/(l(√(2(l_1 ^2 +l_2 ^2 )−l^2 )))) cos α=((OA^2 +OM^2 −AM^2 )/(2×OA×OM)) cos α=((l_1 ^2 +((2(l_1 ^2 +l_2 ^2 )−l^2 )/4)−((l/2))^2 )/(2×l_1 ×((√(2(l_1 ^2 +l_2 ^2 )−l^2 ))/2))) cos α=((3l_1 ^2 +l_2 ^2 −l^2 )/(2l_1 (√(2(l_1 ^2 +l_2 ^2 )−l^2 )))) ⇒α=cos^(−1) ((3l_1 ^2 +l_2 ^2 −l^2 )/(2l_1 (√(2(l_1 ^2 +l_2 ^2 )−l^2 )))) ⇒β=cos^(−1) ((3l_2 ^2 +l_1 ^2 −l^2 )/(2l_2 (√(2(l_1 ^2 +l_2 ^2 )−l^2 ))))

$${let}\:{l}_{\mathrm{1}} ={OA},\:{l}_{\mathrm{2}} ={OB} \\ $$$${we}\:{know}\:{OM}\:{is}\:{a}\:{median}\:{of}\:{the}\:{triangle} \\ $$$${OAB}\:{and} \\ $$$${OM}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} } \\ $$$${cos}\angle{OMB}=\frac{−{l}_{\mathrm{2}} ^{\mathrm{2}} +{OM}^{\mathrm{2}} +{MB}^{\mathrm{2}} }{\mathrm{2}×{OM}×{MB}} \\ $$$${since}\:\theta=\mathrm{90}°−\angle{OMB} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{−{l}_{\mathrm{2}} ^{\mathrm{2}} +{OM}^{\mathrm{2}} +{MB}^{\mathrm{2}} }{\mathrm{2}×{OM}×{MB}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{−{l}_{\mathrm{2}} ^{\mathrm{2}} +\frac{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }{\mathrm{4}}+\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}×\frac{\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }}{\mathrm{2}}×\frac{{l}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{−\mathrm{4}{l}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} +{l}^{\mathrm{2}} }{\mathrm{2}{l}\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{l}_{\mathrm{1}} ^{\mathrm{2}} −{l}_{\mathrm{2}} ^{\mathrm{2}} }{{l}\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \frac{{l}_{\mathrm{1}} ^{\mathrm{2}} −{l}_{\mathrm{2}} ^{\mathrm{2}} }{{l}\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\alpha=\frac{{OA}^{\mathrm{2}} +{OM}^{\mathrm{2}} −{AM}^{\mathrm{2}} }{\mathrm{2}×{OA}×{OM}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{l}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }{\mathrm{4}}−\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}×{l}_{\mathrm{1}} ×\frac{\sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{3}{l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} −{l}^{\mathrm{2}} }{\mathrm{2}{l}_{\mathrm{1}} \sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}{l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} −{l}^{\mathrm{2}} }{\mathrm{2}{l}_{\mathrm{1}} \sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$$$\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}{l}_{\mathrm{2}} ^{\mathrm{2}} +{l}_{\mathrm{1}} ^{\mathrm{2}} −{l}^{\mathrm{2}} }{\mathrm{2}{l}_{\mathrm{2}} \sqrt{\mathrm{2}\left({l}_{\mathrm{1}} ^{\mathrm{2}} +{l}_{\mathrm{2}} ^{\mathrm{2}} \right)−{l}^{\mathrm{2}} }} \\ $$

Commented by ajfour last updated on 23/Jun/18

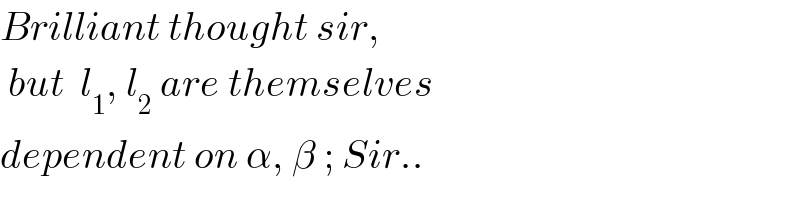
Brilliant thought sir, but l_1 , l_2 are themselves dependent on α, β ; Sir..

$${Brilliant}\:{thought}\:{sir}, \\ $$$$\:{but}\:\:{l}_{\mathrm{1}} ,\:{l}_{\mathrm{2}} \:{are}\:{themselves} \\ $$$${dependent}\:{on}\:\alpha,\:\beta\:;\:{Sir}.. \\ $$

Commented by MrW3 last updated on 23/Jun/18

yes. the problem is still not easy to solve. one can not get a closed formula for case d≠0 to calculate θ directly.

$${yes}.\: \\ $$$${the}\:{problem}\:{is}\:{still}\:{not}\:{easy}\:{to}\:{solve}. \\ $$$${one}\:{can}\:{not}\:{get}\:{a}\:{closed}\:{formula}\:{for} \\ $$$${case}\:{d}\neq\mathrm{0}\:{to}\:{calculate}\:\theta\:{directly}.\: \\ $$

Commented by ajfour last updated on 23/Jun/18

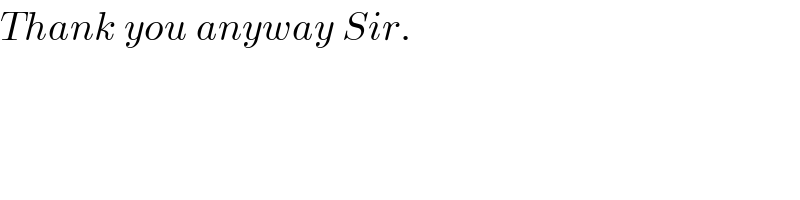
Thank you anyway Sir.

$${Thank}\:{you}\:{anyway}\:{Sir}. \\ $$

Commented by MrW3 last updated on 24/Jun/18

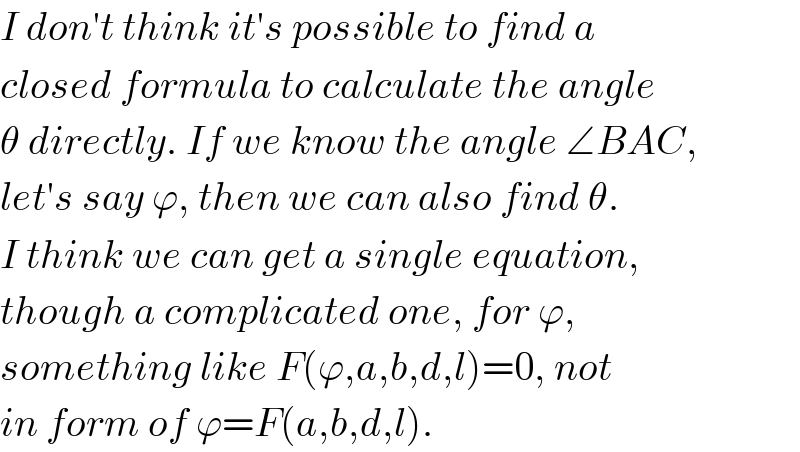
I don′t think it′s possible to find a closed formula to calculate the angle θ directly. If we know the angle ∠BAC, let′s say ϕ, then we can also find θ. I think we can get a single equation, though a complicated one, for ϕ, something like F(ϕ,a,b,d,l)=0, not in form of ϕ=F(a,b,d,l).

$${I}\:{don}'{t}\:{think}\:{it}'{s}\:{possible}\:{to}\:{find}\:{a} \\ $$$${closed}\:{formula}\:{to}\:{calculate}\:{the}\:{angle} \\ $$$$\theta\:{directly}.\:{If}\:{we}\:{know}\:{the}\:{angle}\:\angle{BAC}, \\ $$$${let}'{s}\:{say}\:\varphi,\:{then}\:{we}\:{can}\:{also}\:{find}\:\theta.\: \\ $$$${I}\:{think}\:{we}\:{can}\:{get}\:{a}\:{single}\:{equation}, \\ $$$${though}\:{a}\:{complicated}\:{one},\:{for}\:\varphi, \\ $$$${something}\:{like}\:{F}\left(\varphi,{a},{b},{d},{l}\right)=\mathrm{0},\:{not} \\ $$$${in}\:{form}\:{of}\:\varphi={F}\left({a},{b},{d},{l}\right). \\ $$

Commented by ajfour last updated on 24/Jun/18

Commented by ajfour last updated on 24/Jun/18

{ d_1 +acos α=(l/2)cos θ }×tan 𝛂 {d_2 +bcos β =(l/2)cos θ }×tan β Since d_1 tan α = d_2 tan β =h asin α−bsin β =(l/2)cos θ(tan α−tan β) Now asin α−bsin β = lsin θ _____________________ ⇒ tan 𝛂−tan 𝛃 = 2tan 𝛉 _____________________ Considering the △ with sides a, b, and ρ we have (ρ/(sin (α+β)))=(a/(sin (β+δ)))=(b/(sin (α−δ))) α=sin^(−1) [((bsin (α+β))/ρ)]+δ β=sin^(−1) [((asin (α+β))/ρ)]−δ where (as can easily be seen) 𝛒^2 =(lcos 𝛉−d)^2 +l^2 sin^2 𝛉 tan 𝛅 = ((lsin 𝛉)/(lcos 𝛉−d)) cos (𝛂+𝛃)=((a^2 +b^2 −𝛒^2 )/(2ab)) sin (𝛂+𝛃)=(√(1−[((a^2 +b^2 −𝛒^2 )/(2ab))]^2 )) ρ^2 −b^2 sin^2 (α+β)=ρ^2 −b^2 +(((a^2 +b^2 −ρ^2 )^2 )/(4a^2 )) =((4a^2 (ρ^2 −b^2 )+[a^2 −(ρ^2 −b^2 )]^2 )/(4a^2 )) =[((a^2 +ρ^2 −b^2 )/(2a))]^2 ⇒ 2absin (α+β)=(√(4a^2 b^2 −(a^2 +b^2 −ρ^2 )^2 )) ⇒bsin (α+β)=((√([(a+b)^2 −ρ^2 ][ρ^2 −(a−b)^2 ]))/(2a)) ________________________ 2tan 𝛉 = tan α−tan β =tan {sin^(−1) [((bsin (α+β))/ρ)]+δ} −tan {sin^(−1) [((asin (α+β))/ρ)]−δ} =tan {tan^(−1) (((bsin (α+β))/(√(ρ^2 −b^2 sin^2 (α+β)))))+𝛅} −tan {tan^(−1) (((asin (α+β))/(√(ρ^2 −a^2 sin^2 (α+β))))−𝛅} __________________________ 2tan θ =tan [tan^(−1) ((√([(a+b)^2 −ρ^2 ][ρ^2 −(a−b)^2 ]))/(a^2 +ρ^2 −b^2 ))+δ] −tan [tan^(−1) ((√([(a+b)^2 −ρ^2 ][ρ^2 −(a−b)^2 ]))/(b^2 +ρ^2 −a^2 ))−δ] ___________________________ .

$$\left\{\:\:{d}_{\mathrm{1}} +{a}\mathrm{cos}\:\alpha=\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta\:\:\:\:\right\}×\mathrm{tan}\:\boldsymbol{\alpha} \\ $$$$\:\left\{{d}_{\mathrm{2}} +{b}\mathrm{cos}\:\beta\:=\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta\:\:\:\:\right\}×\mathrm{tan}\:\beta \\ $$$$\:\:\:{Since}\:\:\:{d}_{\mathrm{1}} \mathrm{tan}\:\alpha\:=\:{d}_{\mathrm{2}} \mathrm{tan}\:\beta\:=\boldsymbol{{h}} \\ $$$${a}\mathrm{sin}\:\alpha−{b}\mathrm{sin}\:\beta\:=\frac{{l}}{\mathrm{2}}\mathrm{cos}\:\theta\left(\mathrm{tan}\:\alpha−\mathrm{tan}\:\beta\right) \\ $$$${Now}\:\:\:{a}\mathrm{sin}\:\alpha−{b}\mathrm{sin}\:\beta\:=\:{l}\mathrm{sin}\:\theta \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\:\mathrm{tan}\:\boldsymbol{\alpha}−\mathrm{tan}\:\boldsymbol{\beta}\:=\:\mathrm{2tan}\:\boldsymbol{\theta} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${Considering}\:{the}\:\bigtriangleup\:{with}\:{sides} \\ $$$${a},\:{b},\:{and}\:\rho\:{we}\:{have}\: \\ $$$$\:\:\:\frac{\rho}{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{{a}}{\mathrm{sin}\:\left(\beta+\delta\right)}=\frac{{b}}{\mathrm{sin}\:\left(\alpha−\delta\right)} \\ $$$$\alpha=\mathrm{sin}^{−\mathrm{1}} \left[\frac{{b}\mathrm{sin}\:\left(\alpha+\beta\right)}{\rho}\right]+\delta \\ $$$$\beta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{{a}\mathrm{sin}\:\left(\alpha+\beta\right)}{\rho}\right]−\delta \\ $$$$ \\ $$$${where}\:\left({as}\:{can}\:{easily}\:{be}\:{seen}\right) \\ $$$$\:\:\boldsymbol{\rho}^{\mathrm{2}} =\left(\boldsymbol{{l}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{d}}\right)^{\mathrm{2}} +\boldsymbol{{l}}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta} \\ $$$$\:\:\:\mathrm{tan}\:\boldsymbol{\delta}\:=\:\frac{\boldsymbol{{l}}\mathrm{sin}\:\boldsymbol{\theta}}{\boldsymbol{{l}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{d}}} \\ $$$$\mathrm{cos}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)=\frac{\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{\rho}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{{ab}}} \\ $$$$\mathrm{sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)=\sqrt{\mathrm{1}−\left[\frac{\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{\rho}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{{ab}}}\right]^{\mathrm{2}} }\: \\ $$$$\rho^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\alpha+\beta\right)=\rho^{\mathrm{2}} −{b}^{\mathrm{2}} +\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\rho^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{4}{a}^{\mathrm{2}} \left(\rho^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\left[{a}^{\mathrm{2}} −\left(\rho^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\right]^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\left[\frac{{a}^{\mathrm{2}} +\rho^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{a}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}{ab}\mathrm{sin}\:\left(\alpha+\beta\right)=\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\rho^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow{b}\mathrm{sin}\:\left(\alpha+\beta\right)=\frac{\sqrt{\left[\left({a}+{b}\right)^{\mathrm{2}} −\rho^{\mathrm{2}} \right]\left[\rho^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]}}{\mathrm{2}{a}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\mathrm{2tan}\:\boldsymbol{\theta}\:=\:\mathrm{tan}\:\alpha−\mathrm{tan}\:\beta \\ $$$$\:\:\:\:=\mathrm{tan}\:\left\{\mathrm{sin}^{−\mathrm{1}} \left[\frac{{b}\mathrm{sin}\:\left(\alpha+\beta\right)}{\rho}\right]+\delta\right\} \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{tan}\:\left\{\mathrm{sin}^{−\mathrm{1}} \left[\frac{{a}\mathrm{sin}\:\left(\alpha+\beta\right)}{\rho}\right]−\delta\right\} \\ $$$$\:\:=\mathrm{tan}\:\left\{\mathrm{tan}^{−\mathrm{1}} \left(\frac{{b}\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\rho^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\alpha+\beta\right)}}\right)+\boldsymbol{\delta}\right\} \\ $$$$\:\:\:\:\:\:−\mathrm{tan}\:\left\{\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\rho^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\alpha+\beta\right)}}−\boldsymbol{\delta}\right\}\right. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\mathrm{2tan}\:\theta\: \\ $$$$\:\:=\mathrm{tan}\:\left[\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\left[\left({a}+{b}\right)^{\mathrm{2}} −\rho^{\mathrm{2}} \right]\left[\rho^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]}}{{a}^{\mathrm{2}} +\rho^{\mathrm{2}} −{b}^{\mathrm{2}} }+\delta\right] \\ $$$$\:\:\:\:−\mathrm{tan}\:\left[\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\left[\left({a}+{b}\right)^{\mathrm{2}} −\rho^{\mathrm{2}} \right]\left[\rho^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]}}{{b}^{\mathrm{2}} +\rho^{\mathrm{2}} −{a}^{\mathrm{2}} }−\delta\right]\: \\ $$$$\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:. \\ $$

Commented by MrW3 last updated on 24/Jun/18

this eqn. is correct sir. I checked different values for a,b,d and l. and the solution is right. wonderful working!

$${this}\:{eqn}.\:{is}\:{correct}\:{sir}.\:{I}\:{checked} \\ $$$${different}\:{values}\:{for}\:{a},{b},{d}\:{and}\:{l}.\:{and} \\ $$$${the}\:{solution}\:{is}\:{right}. \\ $$$${wonderful}\:{working}! \\ $$

Commented by ajfour last updated on 25/Jun/18

Thanks you Sir!

$${Thanks}\:{you}\:{Sir}! \\ $$

Answered by ajfour last updated on 24/Jun/18

2tan θ = tan {tan^(−1) [((√([(a+b)^2 −ρ^2 ][ρ^2 −(a−b)^2 ]))/(a^2 +ρ^2 −b^2 ))]+δ} −tan { tan^(−1) [((√([(a+b)^2 −ρ^2 ][ρ^2 −(a−b)^2 ]))/(b^2 +ρ^2 −a^2 ))]−δ} where 𝛒^2 = l^2 sin^2 𝛉+(lcos 𝛉−d)^2 and 𝛅 = tan^(−1) (((lsin 𝛉)/(lcos 𝛉−d))) .

$$\mathrm{2tan}\:\theta \\ $$$$\:=\:{tan}\:\left\{\mathrm{tan}^{−\mathrm{1}} \left[\frac{\sqrt{\left[\left({a}+{b}\right)^{\mathrm{2}} −\rho^{\mathrm{2}} \right]\left[\rho^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]}}{{a}^{\mathrm{2}} +\rho^{\mathrm{2}} −{b}^{\mathrm{2}} }\right]+\delta\right\} \\ $$$$\:\:\:−{tan}\:\left\{\:\mathrm{tan}^{−\mathrm{1}} \left[\frac{\sqrt{\left[\left({a}+{b}\right)^{\mathrm{2}} −\rho^{\mathrm{2}} \right]\left[\rho^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]}}{{b}^{\mathrm{2}} +\rho^{\mathrm{2}} −{a}^{\mathrm{2}} }\right]−\delta\right\} \\ $$$${where} \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{\rho}^{\mathrm{2}} =\:\boldsymbol{{l}}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta}+\left(\boldsymbol{{l}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{d}}\right)^{\mathrm{2}} \\ $$$${and}\:\:\boldsymbol{\delta}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\boldsymbol{{l}}\mathrm{sin}\:\boldsymbol{\theta}}{\boldsymbol{{l}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{d}}}\right)\:. \\ $$

Commented by ajfour last updated on 24/Jun/18

To proceed beyond this , isn′t possible for me. This is all i could arrive at, but ∠BAC or/and ∠ABD is/are eliminated, eventually.

$${To}\:{proceed}\:{beyond}\:{this}\:,\:{isn}'{t} \\ $$$${possible}\:{for}\:{me}.\:{This}\:{is}\:{all}\:{i} \\ $$$${could}\:{arrive}\:{at},\:{but}\:\angle{BAC}\:\:{or}/{and} \\ $$$$\angle{ABD}\:{is}/{are}\:{eliminated},\:{eventually}. \\ $$

Commented by MrW3 last updated on 24/Jun/18

That′s great sir! You have at the end one single equation with only one unknown. The eqn. is even more simple than I ′ve expected.

$${That}'{s}\:{great}\:{sir}!\:{You}\:{have}\:{at}\:{the}\:{end} \\ $$$${one}\:{single}\:{equation}\:{with}\:{only}\:{one} \\ $$$${unknown}.\:{The}\:{eqn}.\:{is}\:{even}\:{more}\:{simple} \\ $$$${than}\:{I}\:'{ve}\:{expected}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com