
Question Number 38106 by maxmathsup by imad last updated on 21/Jun/18
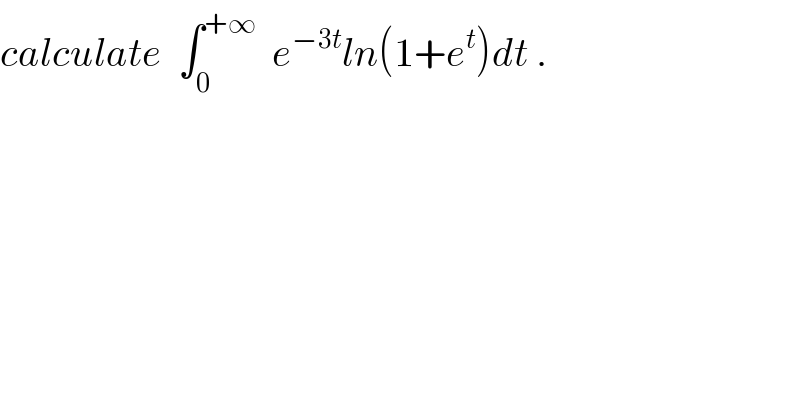
$${calculate}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:{e}^{−\mathrm{3}{t}} {ln}\left(\mathrm{1}+{e}^{{t}} \right){dt}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 08/Jul/18
![by parts u^′ =e^(−3t) and v=ln(1+e^t ) I = [−(1/3)e^(−3t) ln(1+e^t )]_0 ^(+∞) −∫_0 ^(+∞) −(1/3)e^(−3t) (e^t /(1+e^t ))dt =((ln(2))/3) +(1/3) ∫_0 ^∞ (e^(−2t) /(1+e^t )) dt but changement e^t =x give ∫_0 ^∞ (e^(−2t) /(1+e^t )) dt = ∫_1 ^(+∞) (1/(x^2 (1+x))) (dx/x) = ∫_1 ^(+∞) (dx/(x^3 (x+1))) let decompose F(x)= (1/(x^3 (x+1))) F(x) = (a/x) +(b/x^2 ) +(c/x^3 ) +(d/(x+1)) c =lim_(x→0) x^3 F(x)=1 d=lim_(x→−1) (x+1)F(x) =−1 ⇒ F(x) =(a/x) +(b/x^2 ) +(1/x^3 ) −(1/(x+1)) lim_(x→+∞) xF(x) =0=a−1 ⇒a=1 ⇒ F(x) =(1/x) +(b/x^2 ) +(1/x^3 ) −(1/(x+1)) F(1)=(1/2) =1+b +1 −(1/2) =(3/2) +b ⇒ b=−1 ⇒F(x) = (1/x) −(1/x^2 ) + (1/x^3 ) −(1/(x+1)) ⇒ ∫ F(x)dx =ln∣x∣ +(1/x) −(1/(2x^2 )) −ln∣x+1∣ +c ⇒ ∫_1 ^(+∞) F(x)dx =[ (1/x) −(1/(2x^2 ))]_1 ^(+∞) +[ln∣(x/(x+1))∣]_1 ^(+∞) =−1 +(1/2) −ln((1/2))=−(1/2) +ln(2) ⇒ I =((ln(2))/3) +(1/3)(−(1/2) +ln(2)) =(2/3)ln(2) −(1/6) .](Q39619.png)
$${by}\:{parts}\:{u}^{'} \:={e}^{−\mathrm{3}{t}} \:\:{and}\:{v}={ln}\left(\mathrm{1}+{e}^{{t}} \right) \\ $$$$\:{I}\:\:=\:\left[−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} {ln}\left(\mathrm{1}+{e}^{{t}} \right)\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{+\infty} \:−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} \:\:\frac{{e}^{{t}} }{\mathrm{1}+{e}^{{t}} }{dt} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−\mathrm{2}{t}} }{\mathrm{1}+{e}^{{t}} }\:{dt}\:{but}\:{changement} \\ $$$${e}^{{t}} \:={x}\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−\mathrm{2}{t}} }{\mathrm{1}+{e}^{{t}} }\:{dt}\:\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}\:\frac{{dx}}{{x}} \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)\:=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{{x}^{\mathrm{3}} }\:\:+\frac{{d}}{{x}+\mathrm{1}} \\ $$$${c}\:={lim}_{{x}\rightarrow\mathrm{0}} \:{x}^{\mathrm{3}} \:{F}\left({x}\right)=\mathrm{1} \\ $$$${d}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:−\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}={a}−\mathrm{1}\:\Rightarrow{a}=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:−\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:=\mathrm{1}+{b}\:+\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{3}}{\mathrm{2}}\:+{b}\:\:\Rightarrow \\ $$$${b}=−\mathrm{1}\:\Rightarrow{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:={ln}\mid{x}\mid\:+\frac{\mathrm{1}}{{x}}\:\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:−{ln}\mid{x}+\mathrm{1}\mid\:+{c}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:{F}\left({x}\right){dx}\:=\left[\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{+\infty} \:+\left[{ln}\mid\frac{{x}}{{x}+\mathrm{1}}\mid\right]_{\mathrm{1}} ^{+\infty} \\ $$$$=−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\:−{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:+{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${I}\:\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:\:+\frac{\mathrm{1}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\:+{ln}\left(\mathrm{2}\right)\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{ln}\left(\mathrm{2}\right)\:−\frac{\mathrm{1}}{\mathrm{6}}\:. \\ $$
