Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38118 by maxmathsup by imad last updated on 21/Jun/18

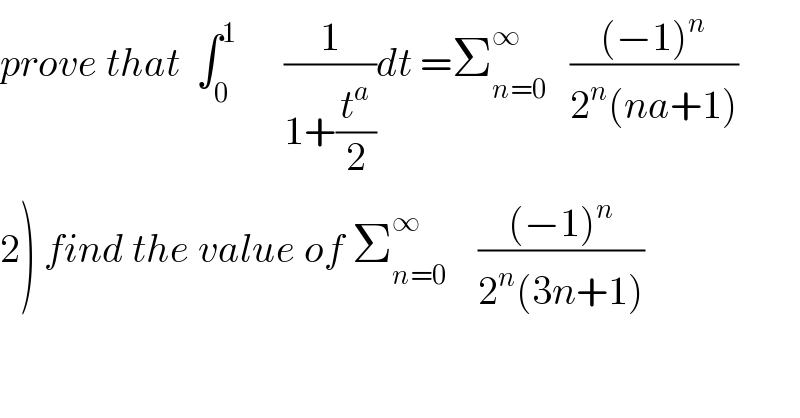
prove that ∫_0 ^1 (1/(1+(t^a /2)))dt =Σ_(n=0) ^∞ (((−1)^n )/(2^n (na+1))) 2) find the value of Σ_(n=0) ^∞ (((−1)^n )/(2^n (3n+1)))

$${prove}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{{a}} }{\mathrm{2}}}{dt}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left({na}+\mathrm{1}\right)} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$

Commented by abdo mathsup 649 cc last updated on 05/Jul/18

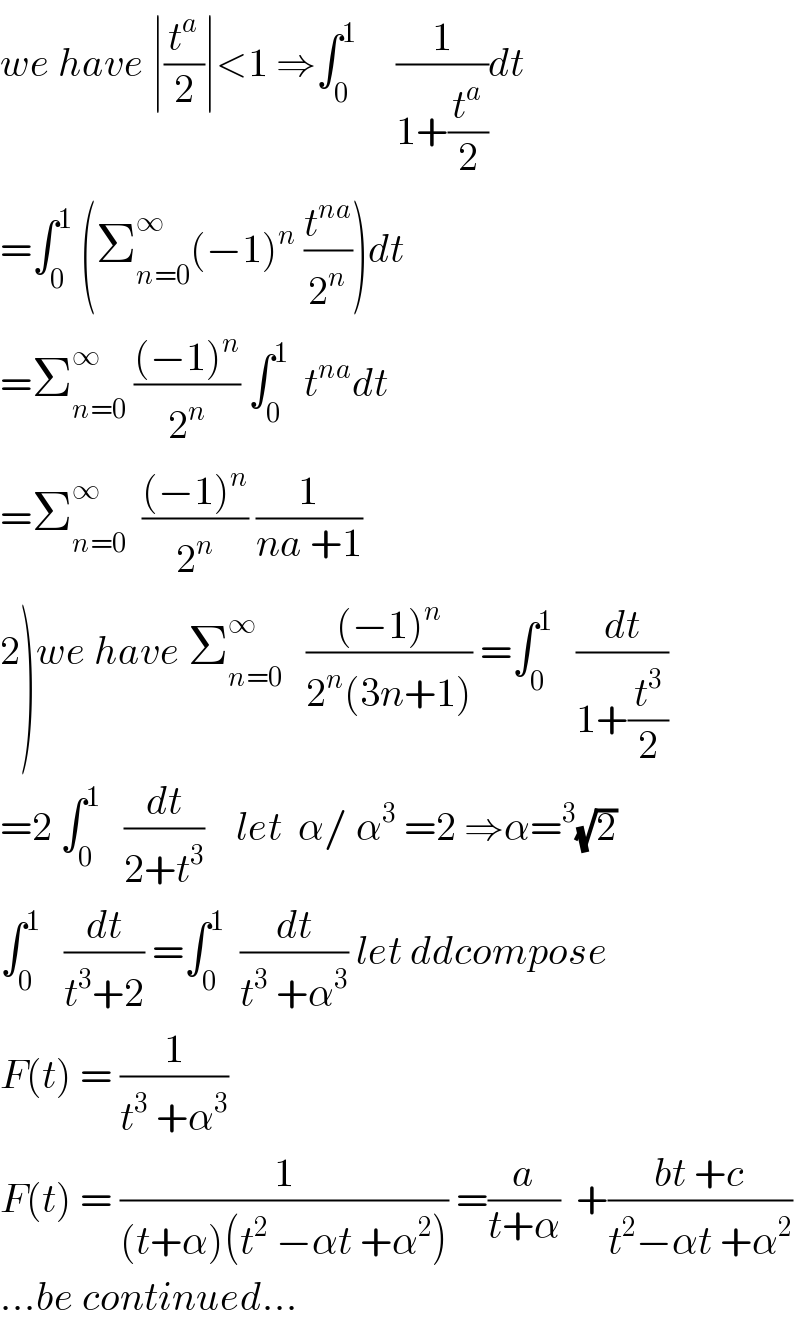
we have ∣(t^a /2)∣<1 ⇒∫_0 ^1 (1/(1+(t^a /2)))dt =∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n (t^(na) /2^n ))dt =Σ_(n=0) ^∞ (((−1)^n )/2^n ) ∫_0 ^1 t^(na) dt =Σ_(n=0) ^∞ (((−1)^n )/2^n ) (1/(na +1)) 2)we have Σ_(n=0) ^∞ (((−1)^n )/(2^n (3n+1))) =∫_0 ^1 (dt/(1+(t^3 /2))) =2 ∫_0 ^1 (dt/(2+t^3 )) let α/ α^3 =2 ⇒α=^3 (√2) ∫_0 ^1 (dt/(t^3 +2)) =∫_0 ^1 (dt/(t^3 +α^3 )) let ddcompose F(t) = (1/(t^3 +α^3 )) F(t) = (1/((t+α)(t^2 −αt +α^2 ))) =(a/(t+α)) +((bt +c)/(t^2 −αt +α^2 )) ...be continued...

$${we}\:{have}\:\mid\frac{{t}^{{a}} }{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{{a}} }{\mathrm{2}}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\frac{{t}^{{na}} }{\mathrm{2}^{{n}} }\right){dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{{na}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\:\frac{\mathrm{1}}{{na}\:+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left(\mathrm{3}{n}+\mathrm{1}\right)}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+\frac{{t}^{\mathrm{3}} }{\mathrm{2}}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{2}+{t}^{\mathrm{3}} }\:\:\:\:{let}\:\:\alpha/\:\alpha^{\mathrm{3}} \:=\mathrm{2}\:\Rightarrow\alpha=^{\mathrm{3}} \sqrt{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{t}^{\mathrm{3}} +\mathrm{2}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\alpha^{\mathrm{3}} }\:{let}\:{ddcompose} \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} \:+\alpha^{\mathrm{3}} } \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\left({t}+\alpha\right)\left({t}^{\mathrm{2}} \:−\alpha{t}\:+\alpha^{\mathrm{2}} \right)}\:=\frac{{a}}{{t}+\alpha}\:\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} −\alpha{t}\:+\alpha^{\mathrm{2}} } \\ $$$$...{be}\:{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com