Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38123 by maxmathsup by imad last updated on 22/Jun/18

f is a function positive and C^1 1) find ∫ (f^′ /(2(√f)(√(1+f))))dx 2)let A_n = ∫_0 ^1 (x^(n/2) /(x(√(1+x^n )))) calculate A_n and lim_(n→+∞) A_n

$${f}\:{is}\:{a}\:{function}\:{positive}\:\:{and}\:{C}^{\mathrm{1}} \:\: \\ $$$$\left.\mathrm{1}\right)\:{find}\:\int\:\:\:\:\frac{{f}^{'} }{\mathrm{2}\sqrt{{f}}\sqrt{\mathrm{1}+{f}}}{dx} \\ $$$$\left.\mathrm{2}\right){let}\:\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\frac{{n}}{\mathrm{2}}} }{{x}\sqrt{\mathrm{1}+{x}^{{n}} }} \\ $$$${calculate}\:{A}_{{n}} \:\:{and}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$

Commented by prof Abdo imad last updated on 22/Jun/18

changement (√f)=u (u function!) give ∫ (f^′ /(2(√f)(√(1+f))))dx=∫ ((2u^′ u)/(2u(√(1+u^2 ))))dx =∫ (u^′ /(√(1+u^2 )))dx=ln(u +(√(1+u^2 ))) +c =ln((√f) +(√(1+f))) +c 2) we have A_n = ∫_0 ^1 (x^(n/2) /(x(√(1+x^n ))))dx changement x^n =t give x=t^(1/n) and A_n = ∫_0 ^1 (t^(1/2) /(t^((1/n) ) (√(1+t)))) (1/n)t^((1/n) −1) dt =(1/n) ∫_0 ^1 (dt/((√t)(√(1+t)))) =_((√t)=u) (1/n)∫_0 ^1 ((2udu)/(u(√(1+u^2 )))) = (2/n)[ln(u +(√(1+u^2 )))]_0 ^1 =(2/n){ ln(1+(√2))}

$${changement}\:\sqrt{{f}}={u}\:\left({u}\:{function}!\right)\:{give} \\ $$$$\int\:\:\frac{{f}^{'} }{\mathrm{2}\sqrt{{f}}\sqrt{\mathrm{1}+{f}}}{dx}=\int\:\frac{\mathrm{2}{u}^{'} {u}}{\mathrm{2}{u}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{dx} \\ $$$$=\int\:\:\:\:\frac{{u}^{'} }{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{dx}={ln}\left({u}\:+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:+{c} \\ $$$$={ln}\left(\sqrt{{f}}\:+\sqrt{\mathrm{1}+{f}}\right)\:+{c}\:\: \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\frac{{n}}{\mathrm{2}}} }{{x}\sqrt{\mathrm{1}+{x}^{{n}} }}{dx}\: \\ $$$${changement}\:{x}^{{n}} ={t}\:{give}\:{x}={t}^{\frac{\mathrm{1}}{{n}}} \:\:{and} \\ $$$${A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}^{\frac{\mathrm{1}}{{n}}\:} \sqrt{\mathrm{1}+{t}}}\:\frac{\mathrm{1}}{{n}}{t}^{\frac{\mathrm{1}}{{n}}\:−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{\sqrt{{t}}\sqrt{\mathrm{1}+{t}}}\:=_{\sqrt{{t}}={u}} \:\:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{udu}}{{u}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$=\:\frac{\mathrm{2}}{{n}}\left[{ln}\left({u}\:+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{{n}}\left\{\:{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right\} \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

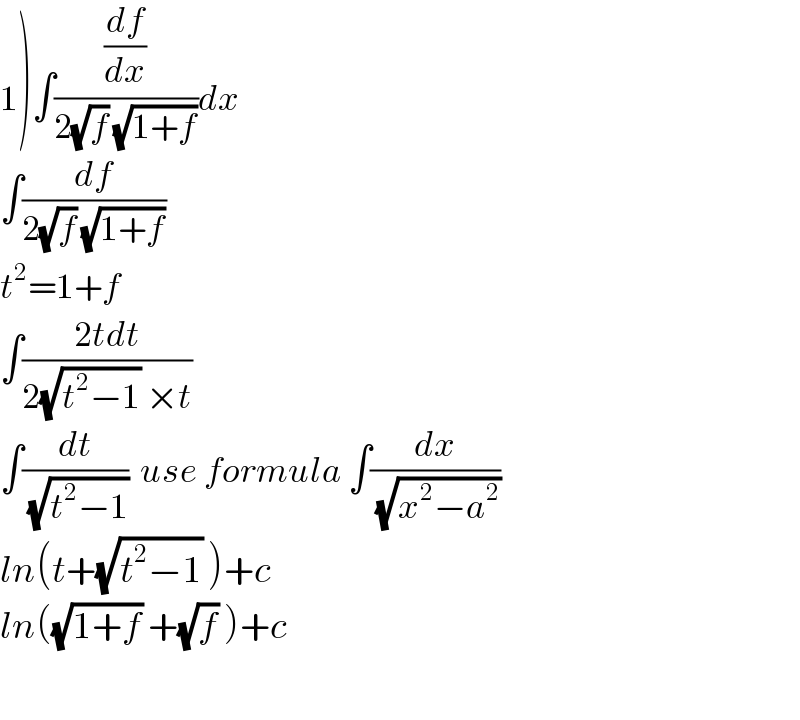
1)∫((df/dx)/(2(√f) (√(1+f))))dx ∫(df/(2(√f) (√(1+f)))) t^2 =1+f ∫((2tdt)/(2(√(t^2 −1)) ×t)) ∫(dt/(√(t^2 −1))) use formula ∫(dx/(√(x^2 −a^2 ))) ln(t+(√(t^2 −1)) )+c ln((√(1+f)) +(√f) )+c

$$\left.\mathrm{1}\right)\int\frac{\frac{{df}}{{dx}}}{\mathrm{2}\sqrt{{f}}\:\sqrt{\mathrm{1}+{f}}}{dx} \\ $$$$\int\frac{{df}}{\mathrm{2}\sqrt{{f}}\:\sqrt{\mathrm{1}+{f}}} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}+{f} \\ $$$$\int\frac{\mathrm{2}{tdt}}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:×{t}} \\ $$$$\int\frac{{dt}}{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:\:{use}\:{formula}\:\int\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }} \\ $$$${ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:\right)+{c} \\ $$$${ln}\left(\sqrt{\mathrm{1}+{f}}\:+\sqrt{{f}}\:\right)+{c} \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

x^n +1=t^2 2tdt =nx^(n−1) dx 2tdt=nx^n (dx/x) ((2tdt)/(n(t^2 −1)))=(dx/x) ∫_1 ^((√2) ) ((2tdt)/(n(t^2 −1)))×(((√(t^2 −1)) )/t) =(2/n)∫_1 ^(√2) (√(t^2 −1)) dt (1/n)∣(t/2)(√(t^2 −1)) −(1/2)ln(t+(√(t^2 −1))) ∣_1 ^((√2) ) (1/n){(((√2) )/2)−(1/2)ln((√2) +1)} =(1/n){(((√2) )/2)−(1/2)ln((√2) +1)} when n→∞ value of intregation is 0 use formula∫(√(x^2 −a^2 )) dx

$${x}^{{n}} +\mathrm{1}={t}^{\mathrm{2}} \:\:\:\:\mathrm{2}{tdt}\:={nx}^{{n}−\mathrm{1}} {dx} \\ $$$$ \\ $$$$\mathrm{2}{tdt}={nx}^{{n}} \frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{2}{tdt}}{{n}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{{dx}}{{x}} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}\:} \frac{\mathrm{2}{tdt}}{{n}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}×\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:}{{t}} \\ $$$$=\frac{\mathrm{2}}{{n}}\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:{dt} \\ $$$$\frac{\mathrm{1}}{{n}}\mid\frac{{t}}{\mathrm{2}}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}+\sqrt{\left.{t}^{\mathrm{2}} −\mathrm{1}\right)}\:\mid_{\mathrm{1}} ^{\sqrt{\mathrm{2}}\:} \right. \\ $$$$\frac{\mathrm{1}}{{n}}\left\{\frac{\sqrt{\mathrm{2}}\:}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{n}}\left\{\frac{\sqrt{\mathrm{2}}\:}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\right\} \\ $$$${when}\:{n}\rightarrow\infty\:\:{value}\:{of}\:{intregation}\:{is}\:\mathrm{0} \\ $$$${use}\:{formula}\int\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \:}\:{dx} \\ $$$$ \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com