Question Number 38126 by maxmathsup by imad last updated on 22/Jun/18
$${calculate}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} \sqrt{\mathrm{1}+{e}^{−\mathrm{4}{x}} }{dx}\:. \\ $$
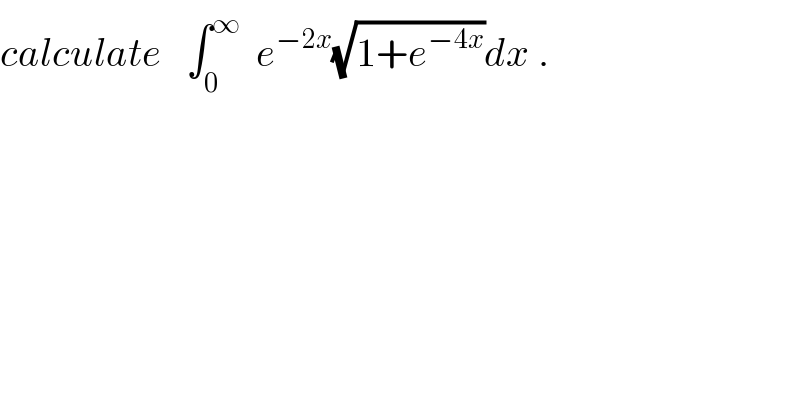
Commented by math khazana by abdo last updated on 26/Jun/18
![let I = ∫_0 ^∞ e^(−2x) (√(1+e^(−4x) ))dx changement e^(−2x) =t give −2x =ln(t)and I = −∫_0 ^1 t(√(1+t^2 ))((−dt)/(2t)) =(1/2) ∫_0 ^1 (√(1+t^2 ))dt 2I =_(t=sh(u)) ∫_0 ^(ln(1 +(√2))) ch(t)ch(t)dt =(1/2) ∫_0 ^(ln(1+(√2))) (1+ch(2t))dt =((ln(1+(√2)))/2) +(1/4) [sh(2t)]_0 ^(ln(1+(√2))) =((ln(1+(√2)))/2) +(1/4)sh(2ln(1+(√2))) =((ln(1+(√2))/2) +(1/8){(1+(√2))^2 −(1+(√2))^(−2) } .](Q38505.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} \sqrt{\mathrm{1}+{e}^{−\mathrm{4}{x}} }{dx}\:{changement} \\ $$$${e}^{−\mathrm{2}{x}} ={t}\:{give}\:−\mathrm{2}{x}\:={ln}\left({t}\right){and}\: \\ $$$${I}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\frac{−{dt}}{\mathrm{2}{t}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\: \\ $$$$\mathrm{2}{I}\:=_{{t}={sh}\left({u}\right)} \:\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}\:+\sqrt{\mathrm{2}}\right)} \:\:{ch}\left({t}\right){ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right.}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} \right\}\:. \\ $$
Commented by math khazana by abdo last updated on 26/Jun/18
$${I}\:=\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{16}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} \right\}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18
$${t}={e}^{−\mathrm{2}{x}\:} \:{dt}=−\mathrm{2}{e}^{−\mathrm{2}{x}} {dx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{0}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{dt} \\ $$$${use}\:{formula}\:\int\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:{dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18
