Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38130 by gunawan last updated on 22/Jun/18

1. ∫tan^3 (2x)sec^5 (2x) dx 2. ∫_0 ^(π/3) tan^5 (x)sec^6 (x) dx 3. ∫tan^6 (ay) dy

$$\mathrm{1}.\:\int\mathrm{tan}^{\mathrm{3}} \left(\mathrm{2}{x}\right)\mathrm{sec}^{\mathrm{5}} \left(\mathrm{2}{x}\right)\:{dx}\: \\ $$$$\mathrm{2}.\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{tan}^{\mathrm{5}} \left({x}\right)\mathrm{sec}^{\mathrm{6}} \left({x}\right)\:{dx}\: \\ $$$$\mathrm{3}.\:\int\mathrm{tan}^{\mathrm{6}} \left({ay}\right)\:{dy}\: \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

1)∫((sin^2 (2x)sin(2x))/(cos^8 (2x)))dx t=cos2x dt=−2sin2xdx =((−1)/2)∫((1−t^2 )/t^8 )×dt =((−1)/2){(t^(−7) /(−7))−(t^(−5) /((−5)))}+c (1/(14))×(1/(cos^7 (2x)))−(1/(10))×(1/(cos^5 (2x)))+c

$$\left.\mathrm{1}\right)\int\frac{{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right){sin}\left(\mathrm{2}{x}\right)}{{cos}^{\mathrm{8}} \left(\mathrm{2}{x}\right)}{dx} \\ $$$${t}={cos}\mathrm{2}{x}\:\:\:{dt}=−\mathrm{2}{sin}\mathrm{2}{xdx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{8}} }×{dt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\left\{\frac{{t}^{−\mathrm{7}} }{−\mathrm{7}}−\frac{{t}^{−\mathrm{5}} }{\left(−\mathrm{5}\right)}\right\}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{14}}×\frac{\mathrm{1}}{{cos}^{\mathrm{7}} \left(\mathrm{2}{x}\right)}−\frac{\mathrm{1}}{\mathrm{10}}×\frac{\mathrm{1}}{{cos}^{\mathrm{5}} \left(\mathrm{2}{x}\right)}+{c} \\ $$

Answered by Joel579 last updated on 22/Jun/18

(3) I = ∫ tan^6 (ay) dy (u = ay → du = a dy) = (1/a) ∫ (sec^2 u − 1)^3 du = (1/a) ∫ (sec^6 u − 3sec^4 u + 3sec^2 u − 1) du

$$\left(\mathrm{3}\right) \\ $$$${I}\:=\:\int\:\mathrm{tan}^{\mathrm{6}} \:\left({ay}\right)\:{dy}\:\:\:\:\left({u}\:=\:{ay}\:\:\rightarrow\:\:{du}\:=\:{a}\:{dy}\right) \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\left(\mathrm{sec}^{\mathrm{2}} \:{u}\:−\:\mathrm{1}\right)^{\mathrm{3}} \:{du} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\left(\mathrm{sec}^{\mathrm{6}} \:{u}\:−\:\mathrm{3sec}^{\mathrm{4}} \:{u}\:+\:\mathrm{3sec}^{\mathrm{2}} \:{u}\:−\:\mathrm{1}\right)\:{du} \\ $$

Commented by Joel579 last updated on 22/Jun/18

Answered by Joel579 last updated on 22/Jun/18

(3) I = ∫ tan^6 (ay) dy (u = ay → du = a dy) = (1/a) ∫ tan^2 u . tan^4 u du = (1/a) ∫ (sec^2 u . tan^4 u − tan^4 u) du = (1/a) ∫ [sec^2 u . tan^4 u − (sec^2 u − 1)tan^2 u] du = (1/a) ∫ [sec^2 u . tan^4 u − sec^2 u . tan^2 u] du + ∫ tan^2 u du t = tan u → dt = sec^2 u du I = (1/a) ∫ t^4 − t^2 dt + tan u − u = (1/a)((t^5 /5) − (t^3 /3) + tan u − u) + C

$$\left(\mathrm{3}\right) \\ $$$${I}\:=\:\int\:\mathrm{tan}^{\mathrm{6}} \:\left({ay}\right)\:{dy}\:\:\:\left({u}\:=\:{ay}\:\:\rightarrow\:\:{du}\:=\:{a}\:{dy}\right) \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\mathrm{tan}^{\mathrm{2}} \:{u}\:.\:\mathrm{tan}^{\mathrm{4}} \:{u}\:{du} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\left(\mathrm{sec}^{\mathrm{2}} \:{u}\:.\:\mathrm{tan}^{\mathrm{4}} \:{u}\:−\:\mathrm{tan}^{\mathrm{4}} \:{u}\right)\:{du} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\left[\mathrm{sec}^{\mathrm{2}} \:{u}\:.\:\mathrm{tan}^{\mathrm{4}} \:{u}\:−\:\left(\mathrm{sec}^{\mathrm{2}} \:{u}\:−\:\mathrm{1}\right)\mathrm{tan}^{\mathrm{2}} \:{u}\right]\:{du} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\:\int\:\left[\mathrm{sec}^{\mathrm{2}} \:{u}\:.\:\mathrm{tan}^{\mathrm{4}} \:{u}\:−\:\mathrm{sec}^{\mathrm{2}} \:{u}\:.\:\mathrm{tan}^{\mathrm{2}} \:{u}\right]\:{du}\:+\:\int\:\mathrm{tan}^{\mathrm{2}} \:{u}\:{du} \\ $$$${t}\:=\:\mathrm{tan}\:{u}\:\:\rightarrow\:\:{dt}\:=\:\mathrm{sec}^{\mathrm{2}} \:{u}\:{du} \\ $$$${I}\:=\:\frac{\mathrm{1}}{{a}}\:\int\:{t}^{\mathrm{4}} \:−\:{t}^{\mathrm{2}} \:{dt}\:+\:\mathrm{tan}\:{u}\:−\:{u} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{{a}}\left(\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\:−\:\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:+\:\mathrm{tan}\:{u}\:−\:{u}\right)\:+\:{C} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

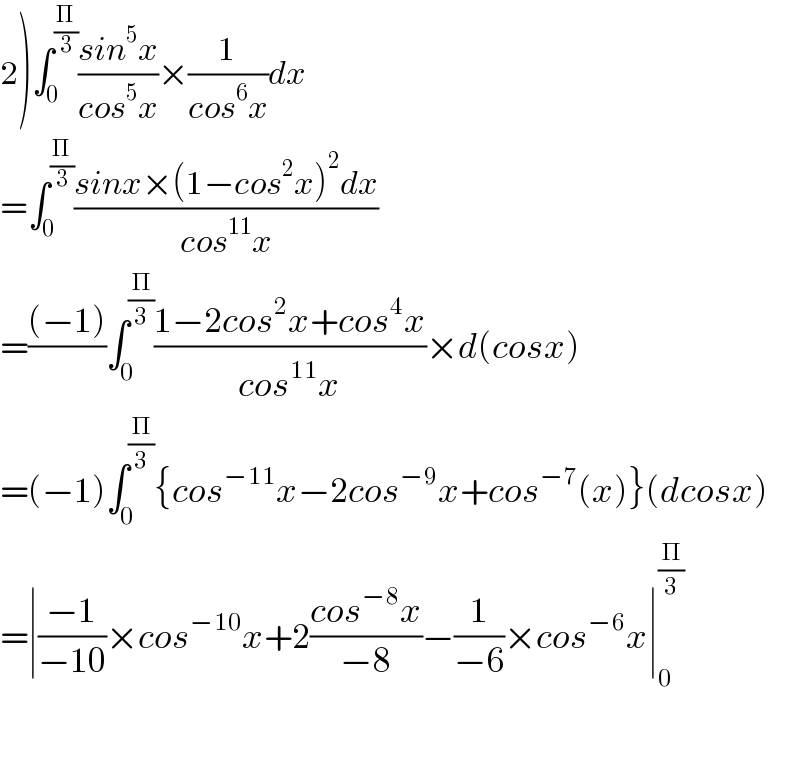
2)∫_0 ^(Π/3) ((sin^5 x)/(cos^5 x))×(1/(cos^6 x))dx =∫_0 ^(Π/3) ((sinx×(1−cos^2 x)^2 dx)/(cos^(11) x)) =(((−1))/)∫_0 ^(Π/3) ((1−2cos^2 x+cos^4 x)/(cos^(11) x))×d(cosx) =(−1)∫_0 ^(Π/3) {cos^(−11) x−2cos^(−9) x+cos^(−7) (x)}(dcosx) =∣((−1)/(−10))×cos^(−10) x+2((cos^(−8) x)/(−8))−(1/(−6))×cos^(−6) x∣_0 ^(Π/3)

$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{3}}} \frac{{sin}^{\mathrm{5}} {x}}{{cos}^{\mathrm{5}} {x}}×\frac{\mathrm{1}}{{cos}^{\mathrm{6}} {x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{3}}} \frac{{sinx}×\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} {dx}}{{cos}^{\mathrm{11}} {x}} \\ $$$$=\frac{\left(−\mathrm{1}\right)}{}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{3}}} \frac{\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}+{cos}^{\mathrm{4}} {x}}{{cos}^{\mathrm{11}} {x}}×{d}\left({cosx}\right) \\ $$$$=\left(−\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{3}}} \left\{{cos}^{−\mathrm{11}} {x}−\mathrm{2}{cos}^{−\mathrm{9}} {x}+{cos}^{−\mathrm{7}} \left({x}\right)\right\}\left({dcosx}\right) \\ $$$$=\mid\frac{−\mathrm{1}}{−\mathrm{10}}×{cos}^{−\mathrm{10}} {x}+\mathrm{2}\frac{{cos}^{−\mathrm{8}} {x}}{−\mathrm{8}}−\frac{\mathrm{1}}{−\mathrm{6}}×{cos}^{−\mathrm{6}} {x}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{3}}} \\ $$$$ \\ $$

Commented by gunawan last updated on 22/Jun/18

Thank You very much Sir

$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com