
Question and Answers Forum
Question Number 38181 by rahul 19 last updated on 22/Jun/18
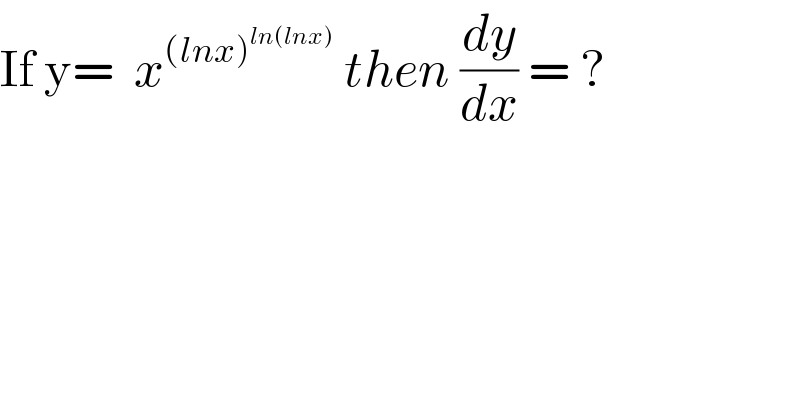
Commented by rahul 19 last updated on 22/Jun/18
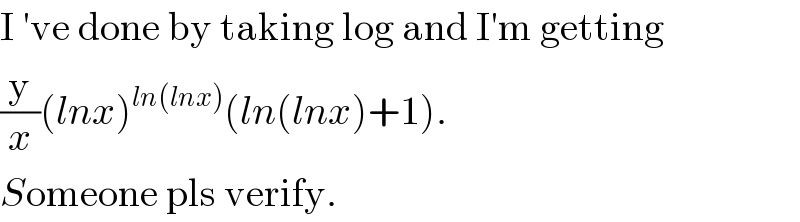
Commented by MJS last updated on 23/Jun/18
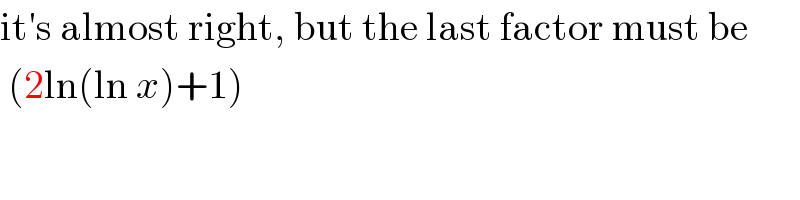
Commented by abdo mathsup 649 cc last updated on 23/Jun/18
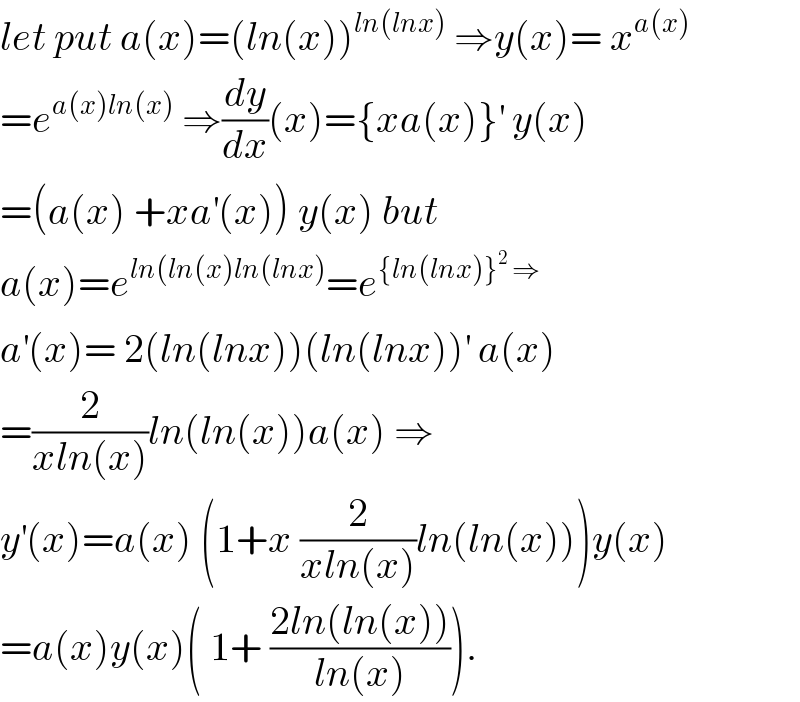
Answered by MJS last updated on 23/Jun/18
![(d/dx)[x^(f(x)) ]=x^(f(x)) ×(((f(x))/x)+(d/dx)[f(x)]×ln x) f(x)=(ln x)^(g(x)) (d/dx)[f(x)]=(ln x)^(g(x)) ×(((g(x))/(xln x))+(d/dx)[g(x)]×ln(ln x)) g(x)=ln(ln x) (d/dx)[g(x)]=(1/(xln x)) (d/dx)[f(x)]=(ln x)^(ln(ln x)) ×(((ln(ln x))/(xln x))+(1/(xln x))×ln(ln x))= =2((ln(ln x))/(xln x))(ln x)^(ln(ln x)) (d/dx)[x^(f(x)) ]=x^((ln x)^(ln(ln x)) ) ×((((ln x)^(ln(ln x)) )/x)+2((ln(ln x))/(xln x))(ln x)^(ln(ln x)) ×ln x)= =(1+2ln(ln x))(ln x)^(ln(ln x)) x^((ln x)^(ln(ln x)) −1)](Q38214.png)
Answered by rahul 19 last updated on 23/Jun/18
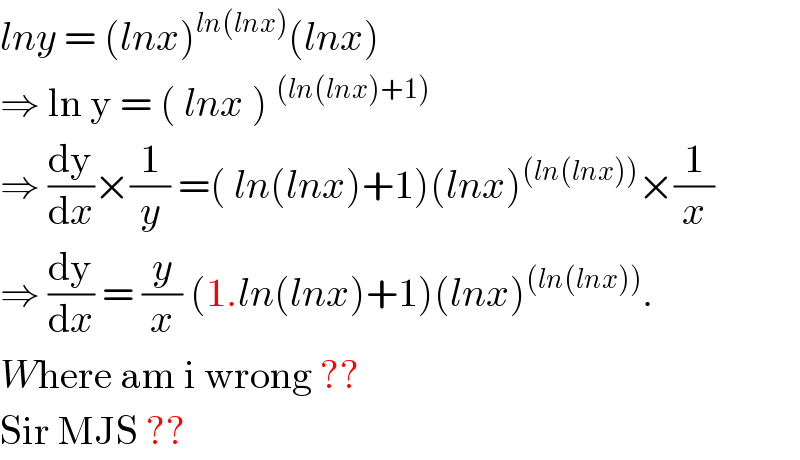
Commented by MJS last updated on 23/Jun/18
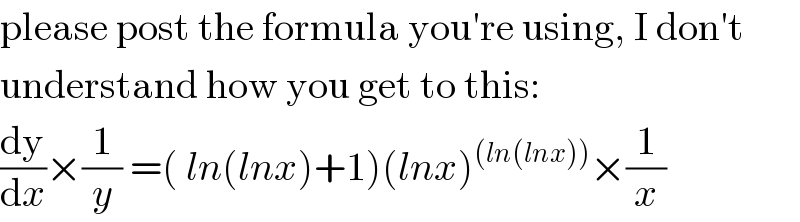
Commented by rahul 19 last updated on 24/Jun/18
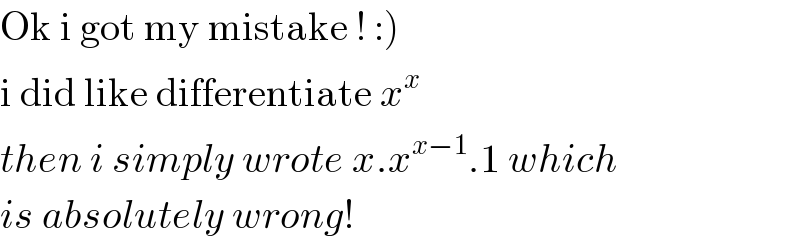
Commented by MJS last updated on 24/Jun/18

