
Question and Answers Forum
Question Number 38197 by maxmathsup by imad last updated on 22/Jun/18
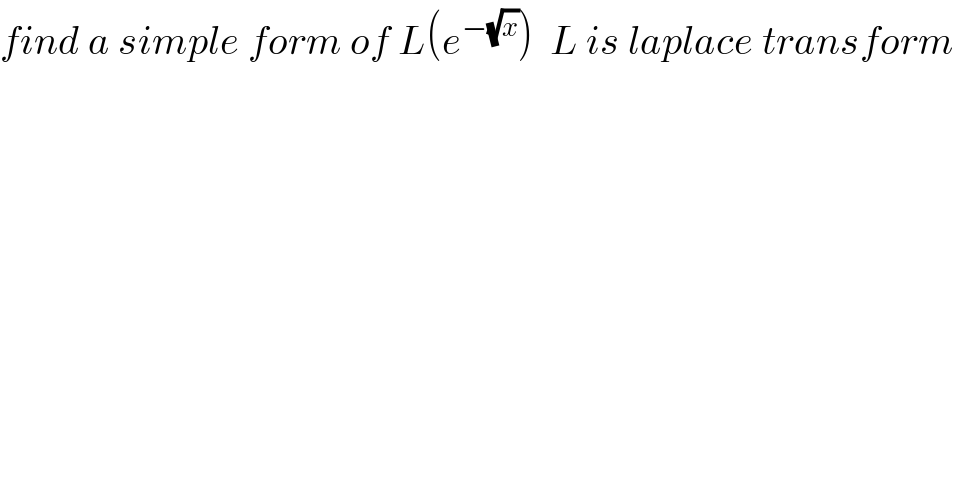
Commented by math khazana by abdo last updated on 25/Jun/18
![L(e^(−(√x)) )= ∫_0 ^∞ f(t)e^(−xt) dt=∫_0 ^∞ e^(−(√t) −xt) dt changement (√t)=u give L(e^(−(√x)) )= ∫_0 ^∞ e^(−u−xu^2 ) 2u du =−(1/x) ∫_0 ^∞ −2xu e^(−xu^2 ) e^(−u) du −(1/x){[ e^(−xu^2 ) e^(−u) ]_0 ^(+∞) +∫_0 ^∞ e^(−u) e^(−xu^2 ) } =(1/x) −(1/x) ∫_0 ^∞ e^(−(xu^2 +u)) du but ∫_0 ^∞ e^(−(xu^2 +u)) du=∫_0 ^∞ e^(−{((√x)u)^2 +2 (((√x)u)/(√x)) + (1/x) −(1/x)}) du = ∫_0 ^∞ e^(−{ ((√x)u +(1/(√x)))^2 } +(1/x)) du =e^(1/x) ∫_0 ^∞ e^(−{ ((√x)u+(1/(√x)))^2 }) du =e^(1/x) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) (dt/(√x)) ( chang.(√x)u +(1/(√x)) =t) =(e^(1/x) /(√x)) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) dt ⇒ L(e^(−(√x)) ) =(1/x) −(e^(1/(√x)) /(x(√x))) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) dt .](Q38438.png)
| ||
Question and Answers Forum | ||
Question Number 38197 by maxmathsup by imad last updated on 22/Jun/18 | ||
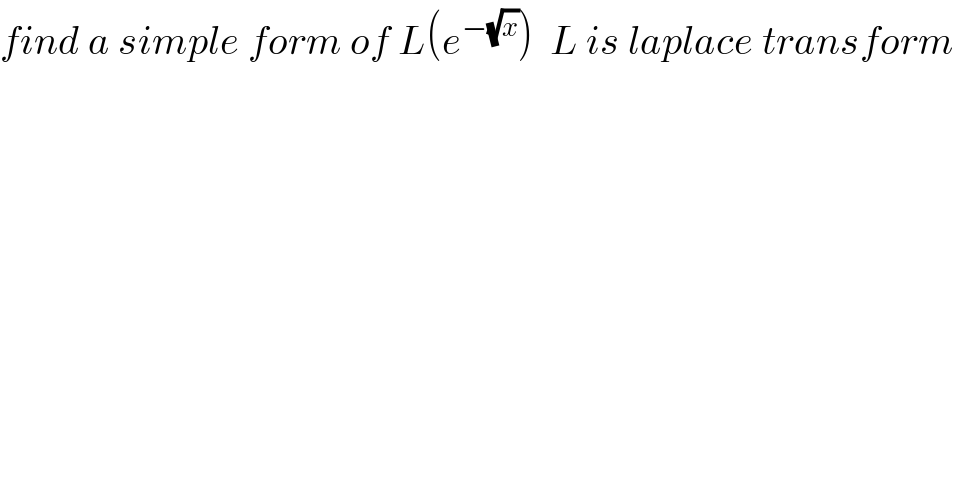 | ||
Commented by math khazana by abdo last updated on 25/Jun/18 | ||
![L(e^(−(√x)) )= ∫_0 ^∞ f(t)e^(−xt) dt=∫_0 ^∞ e^(−(√t) −xt) dt changement (√t)=u give L(e^(−(√x)) )= ∫_0 ^∞ e^(−u−xu^2 ) 2u du =−(1/x) ∫_0 ^∞ −2xu e^(−xu^2 ) e^(−u) du −(1/x){[ e^(−xu^2 ) e^(−u) ]_0 ^(+∞) +∫_0 ^∞ e^(−u) e^(−xu^2 ) } =(1/x) −(1/x) ∫_0 ^∞ e^(−(xu^2 +u)) du but ∫_0 ^∞ e^(−(xu^2 +u)) du=∫_0 ^∞ e^(−{((√x)u)^2 +2 (((√x)u)/(√x)) + (1/x) −(1/x)}) du = ∫_0 ^∞ e^(−{ ((√x)u +(1/(√x)))^2 } +(1/x)) du =e^(1/x) ∫_0 ^∞ e^(−{ ((√x)u+(1/(√x)))^2 }) du =e^(1/x) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) (dt/(√x)) ( chang.(√x)u +(1/(√x)) =t) =(e^(1/x) /(√x)) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) dt ⇒ L(e^(−(√x)) ) =(1/x) −(e^(1/(√x)) /(x(√x))) ∫_(1/(√x)) ^(+∞) e^(−t^2 ) dt .](Q38438.png) | ||