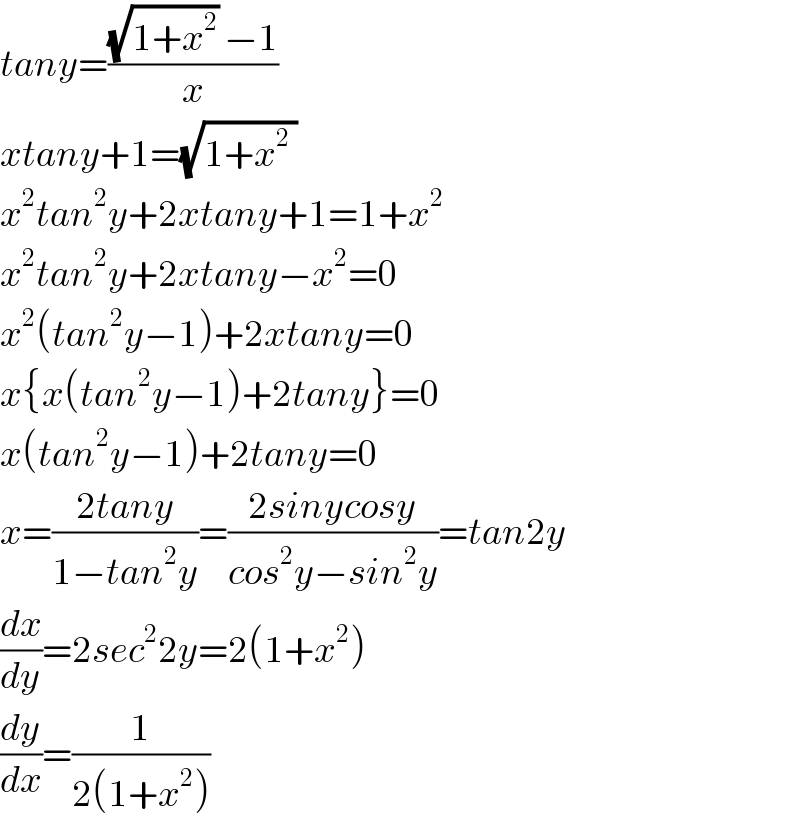Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 38232 by rahul 19 last updated on 23/Jun/18

Differentiate tan^(−1) ((((√(1+x^2 ))−1)/x)) without using any trigonometric substitution !

$$\mathrm{Differentiate}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\right)\:\: \\ $$$${without}\:{using}\:{any}\:{trigonometric}\: \\ $$$${substitution}\:! \\ $$

Commented by math khazana by abdo last updated on 23/Jun/18

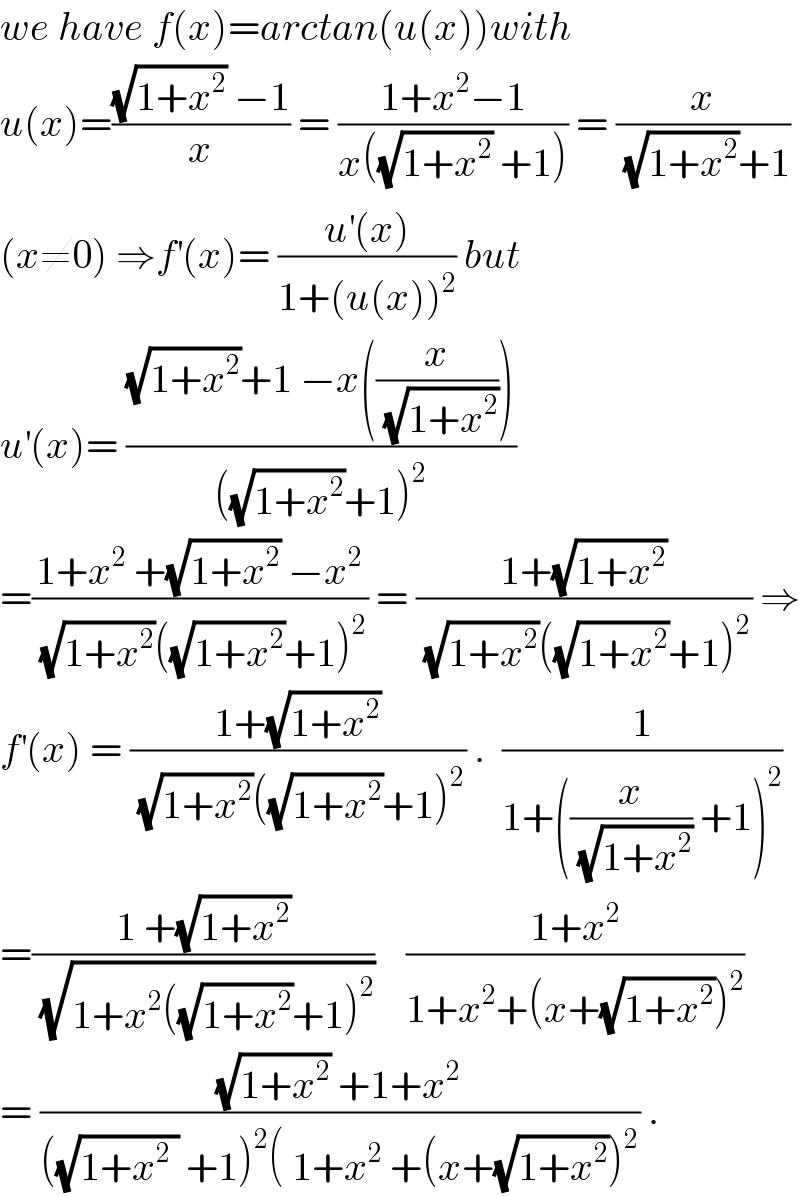
we have f(x)=arctan(u(x))with u(x)=(((√(1+x^2 )) −1)/x) = ((1+x^2 −1)/(x((√(1+x^2 )) +1))) = (x/((√(1+x^2 ))+1)) (x≠0) ⇒f^′ (x)= ((u^′ (x))/(1+(u(x))^2 )) but u^′ (x)= (((√(1+x^2 ))+1 −x((x/(√(1+x^2 )))))/(((√(1+x^2 ))+1)^2 )) =((1+x^2 +(√(1+x^2 )) −x^2 )/((√(1+x^2 ))((√(1+x^2 ))+1)^2 )) = ((1+(√(1+x^2 )))/((√(1+x^2 ))((√(1+x^2 ))+1)^2 )) ⇒ f^′ (x) = ((1+(√(1+x^2 )))/((√(1+x^2 ))((√(1+x^2 ))+1)^2 )) . (1/(1+((x/(√(1+x^2 ))) +1)^2 )) =((1 +(√(1+x^2 )))/(√(1+x^2 ((√(1+x^2 ))+1)^2 ))) ((1+x^2 )/(1+x^2 +(x+(√(1+x^2 )))^2 )) = (((√(1+x^2 )) +1+x^2 )/(((√(1+x^2 )) +1)^2 ( 1+x^2 +(x+(√(1+x^2 )))^2 )) .

$${we}\:{have}\:{f}\left({x}\right)={arctan}\left({u}\left({x}\right)\right){with}\: \\ $$$${u}\left({x}\right)=\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}}{{x}}\:=\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{{x}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\mathrm{1}\right)}\:=\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}} \\ $$$$\left({x}\neq\mathrm{0}\right)\:\Rightarrow{f}^{'} \left({x}\right)=\:\frac{{u}^{'} \left({x}\right)}{\mathrm{1}+\left({u}\left({x}\right)\right)^{\mathrm{2}} }\:{but} \\ $$$${u}^{'} \left({x}\right)=\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\:−{x}\left(\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)}{\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}+{x}^{\mathrm{2}} \:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\:.\:\:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }}\:\:\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} +\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\mathrm{1}+{x}^{\mathrm{2}} }{\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:+\mathrm{1}\right)^{\mathrm{2}} \left(\:\mathrm{1}+{x}^{\mathrm{2}} \:+\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \right.}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jun/18

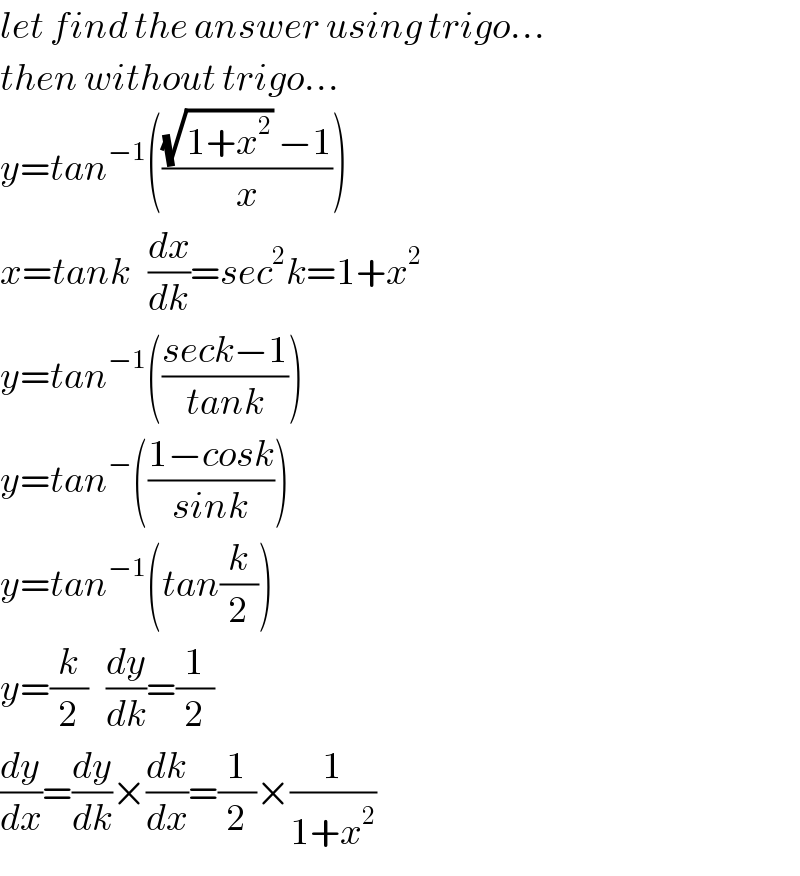
let find the answer using trigo... then without trigo... y=tan^(−1) ((((√(1+x^2 )) −1)/x)) x=tank (dx/dk)=sec^2 k=1+x^2 y=tan^(−1) (((seck−1)/(tank))) y=tan^− (((1−cosk)/(sink))) y=tan^(−1) (tan(k/2)) y=(k/2) (dy/dk)=(1/2) (dy/dx)=(dy/dk)×(dk/dx)=(1/2)×(1/(1+x^2 ))

$${let}\:{find}\:{the}\:{answer}\:{using}\:{trigo}... \\ $$$${then}\:{without}\:{trigo}... \\ $$$${y}={tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}}{{x}}\right) \\ $$$${x}={tank}\:\:\:\frac{{dx}}{{dk}}={sec}^{\mathrm{2}} {k}=\mathrm{1}+{x}^{\mathrm{2}} \\ $$$${y}={tan}^{−\mathrm{1}} \left(\frac{{seck}−\mathrm{1}}{{tank}}\right) \\ $$$${y}={tan}^{−} \left(\frac{\mathrm{1}−{cosk}}{{sink}}\right) \\ $$$${y}={tan}^{−\mathrm{1}} \left({tan}\frac{{k}}{\mathrm{2}}\right) \\ $$$${y}=\frac{{k}}{\mathrm{2}}\:\:\:\frac{{dy}}{{dk}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dk}}×\frac{{dk}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$

Answered by MJS last updated on 23/Jun/18

(d/dx)[arctan x]=(1/(x^2 +1)) this is a standard derivate... we get it this way: arctan x=f(x) x=tan(f(x)) (d/dx)[x]=(d/dx)[tan(f(x))] 1=sec^2 (f(x))f′(x) 1=sec^2 (arctan x)f′(x) f′(x)=(1/(sec^2 (arctan x))) sec^2 α=(1/(cos^2 α))=((sin^2 α +cos^2 α)/(cos^2 α))=tan^2 α +1 f′(x)=(1/(tan^2 (arctan x)+1))=(1/(x^2 +1)) (d/dx)[arctan (((√(1+x^2 ))−1)/x)]= =(((d/dx)[(((√(1+x^2 ))−1)/x)])/(((((√(1+x^2 ))−1)/x))^2 +1))=((((√(1+x^2 ))−1)/(x^2 (√(1+x^2 ))))/(2((1+x^2 −(√(1+x^2 )))/x^2 )))= =(1/(2(1+x^2 )))

$$\frac{{d}}{{dx}}\left[\mathrm{arctan}\:{x}\right]=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{standard}\:\mathrm{derivate}... \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{it}\:\mathrm{this}\:\mathrm{way}: \\ $$$$\mathrm{arctan}\:{x}={f}\left({x}\right) \\ $$$${x}=\mathrm{tan}\left({f}\left({x}\right)\right) \\ $$$$\frac{{d}}{{dx}}\left[{x}\right]=\frac{{d}}{{dx}}\left[\mathrm{tan}\left({f}\left({x}\right)\right)\right] \\ $$$$\mathrm{1}=\mathrm{sec}^{\mathrm{2}} \left({f}\left({x}\right)\right){f}'\left({x}\right) \\ $$$$\mathrm{1}=\mathrm{sec}^{\mathrm{2}} \left(\mathrm{arctan}\:{x}\right){f}'\left({x}\right) \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{arctan}\:{x}\right)} \\ $$$$\mathrm{sec}^{\mathrm{2}} \:\alpha=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\alpha}=\frac{\mathrm{sin}^{\mathrm{2}} \:\alpha\:+\mathrm{cos}^{\mathrm{2}} \:\alpha}{\mathrm{cos}^{\mathrm{2}} \:\alpha}=\mathrm{tan}^{\mathrm{2}} \:\alpha\:+\mathrm{1} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \left(\mathrm{arctan}\:{x}\right)+\mathrm{1}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$ \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\right]= \\ $$$$=\frac{\frac{{d}}{{dx}}\left[\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\right]}{\left(\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}{\mathrm{2}\frac{\mathrm{1}+{x}^{\mathrm{2}} −\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$

Answered by ajfour last updated on 23/Jun/18

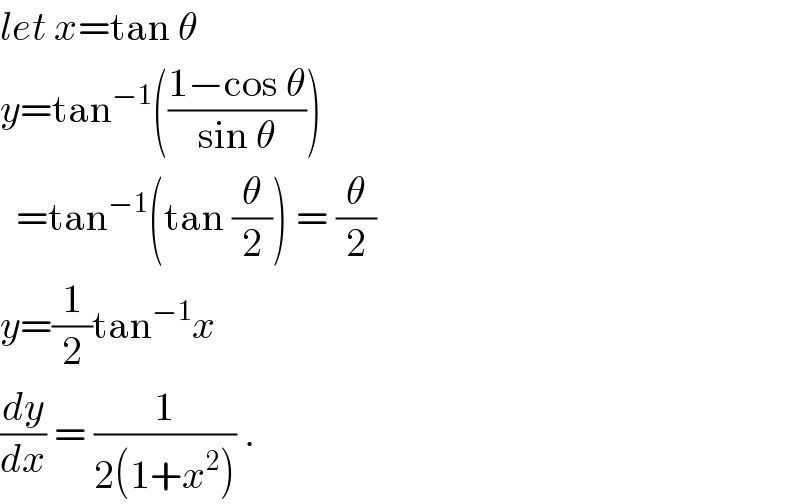
let x=tan θ y=tan^(−1) (((1−cos θ)/(sin θ))) =tan^(−1) (tan (θ/2)) = (θ/2) y=(1/2)tan^(−1) x (dy/dx) = (1/(2(1+x^2 ))) .

$${let}\:{x}=\mathrm{tan}\:\theta \\ $$$${y}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\right) \\ $$$$\:\:=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)\:=\:\frac{\theta}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jun/18

tany=(((√(1+x^2 )) −1)/x) xtany+1=(√(1+x^2 )) x^2 tan^2 y+2xtany+1=1+x^2 x^2 tan^2 y+2xtany−x^2 =0 x^2 (tan^2 y−1)+2xtany=0 x{x(tan^2 y−1)+2tany}=0 x(tan^2 y−1)+2tany=0 x=((2tany)/(1−tan^2 y))=((2sinycosy)/(cos^2 y−sin^2 y))=tan2y (dx/dy)=2sec^2 2y^ =2(1+x^2 ) (dy/dx)=(1/(2(1+x^2 )))

$${tany}=\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}}{{x}} \\ $$$${xtany}+\mathrm{1}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:} \\ $$$${x}^{\mathrm{2}} {tan}^{\mathrm{2}} {y}+\mathrm{2}{xtany}+\mathrm{1}=\mathrm{1}+{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {tan}^{\mathrm{2}} {y}+\mathrm{2}{xtany}−{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({tan}^{\mathrm{2}} {y}−\mathrm{1}\right)+\mathrm{2}{xtany}=\mathrm{0} \\ $$$${x}\left\{{x}\left({tan}^{\mathrm{2}} {y}−\mathrm{1}\right)+\mathrm{2}{tany}\right\}=\mathrm{0} \\ $$$${x}\left({tan}^{\mathrm{2}} {y}−\mathrm{1}\right)+\mathrm{2}{tany}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}{tany}}{\mathrm{1}−{tan}^{\mathrm{2}} {y}}=\frac{\mathrm{2}{sinycosy}}{{cos}^{\mathrm{2}} {y}−{sin}^{\mathrm{2}} {y}}={tan}\mathrm{2}{y} \\ $$$$\frac{{dx}}{{dy}}=\mathrm{2}{sec}^{\mathrm{2}} \mathrm{2}\overset{} {{y}}=\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com