Question and Answers Forum
Question Number 38247 by ajfour last updated on 23/Jun/18

Commented by ajfour last updated on 23/Jun/18
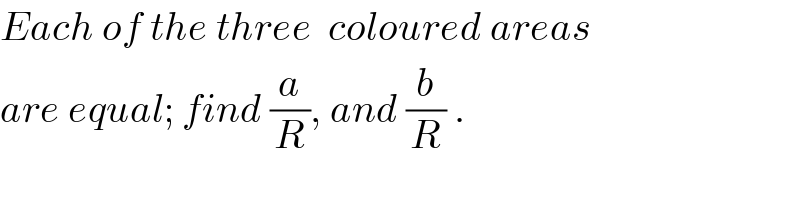
Commented by behi83417@gmail.com last updated on 23/Jun/18

Answered by behi83417@gmail.com last updated on 25/Jun/18
![eq. of circle: x^2 +y^2 =R^2 z^2 =R^2 −b^2 ⇒z=(√(R^2 −b^2 )) S_z =∫_(−b) ^0 [((√(R^2 −x^2 ))−((√(R^2 −b^2 )))]dx= =[−(x/2)(√(R^2 −x^2 ))+(R^2 /2)sin^(−1) (x/R)−x(√(R^2 −b^2 ))]_(−b) ^0 = =[(R^2 /2)sin^(−1) (b/R)−((3b)/2)(√(R^2 −b^2 ))] S_(pink) =((πR^2 )/4)+b^2 +2b(√(R^2 −b^2 ))+2S_z S_(blue) =((3πR^2 )/4)−b^2 −2b(√(R^2 −b^2 ))−2S_z ⇒((πR^2 )/2)−2b^2 −4b(√(R^2 −b^2 ))=4S_z ((πR^2 )/2)−2b^2 −4b(√(R^2 −b^2 ))=2R^2 sin^(−1) (b/R)−6b(√(R^2 −b^2 )) ((πR^2 )/2)−2b^2 +2b(√(R^2 −b^2 ))−2R^2 sin^(−1) (b/R)=0 π−4(b^2 /R^2 )+4(b/R)(√(1−(b^2 /R^2 )))−4sin^(−1) (b/R)=0 ⇒^((b/R)=m) m^2 −m(√(1−m^2 ))+sin^(−1) m−(π/4)=0 ⇒m=(b/R)=0.71](Q38388.png)
Commented by behi83417@gmail.com last updated on 25/Jun/18
Commented by ajfour last updated on 25/Jun/18
Commented by MrW3 last updated on 25/Jun/18
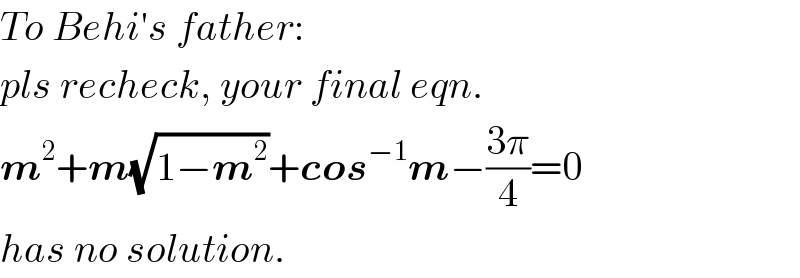
Commented by MrW3 last updated on 25/Jun/18
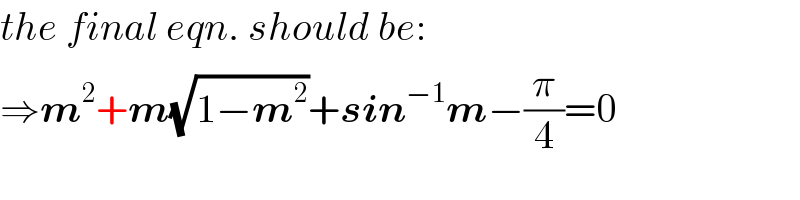
Answered by MrW3 last updated on 25/Jun/18
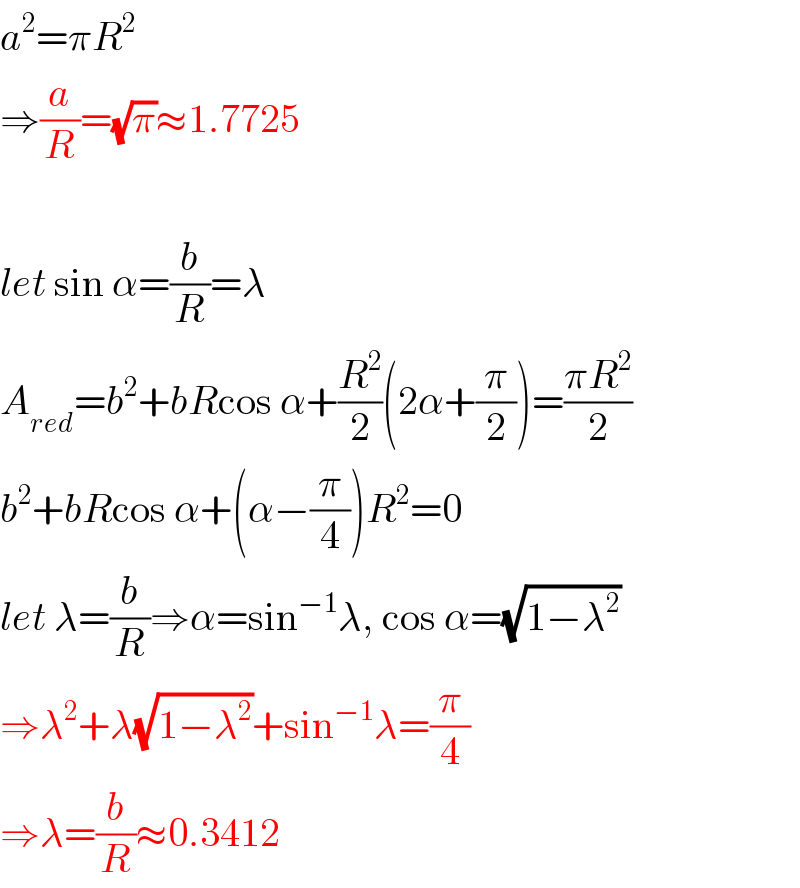
Commented by behi83417@gmail.com last updated on 25/Jun/18

Commented by ajfour last updated on 25/Jun/18