Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 38284 by NECx last updated on 23/Jun/18

Find all the complex number in the rectangular form such that (z−1)^4 =−1

$${Find}\:{all}\:{the}\:{complex}\:{number}\:{in}\:{the} \\ $$$${rectangular}\:{form}\:{such}\:{that} \\ $$$$\left({z}−\mathrm{1}\right)^{\mathrm{4}} =−\mathrm{1} \\ $$$$ \\ $$

Commented by MrW3 last updated on 23/Jun/18

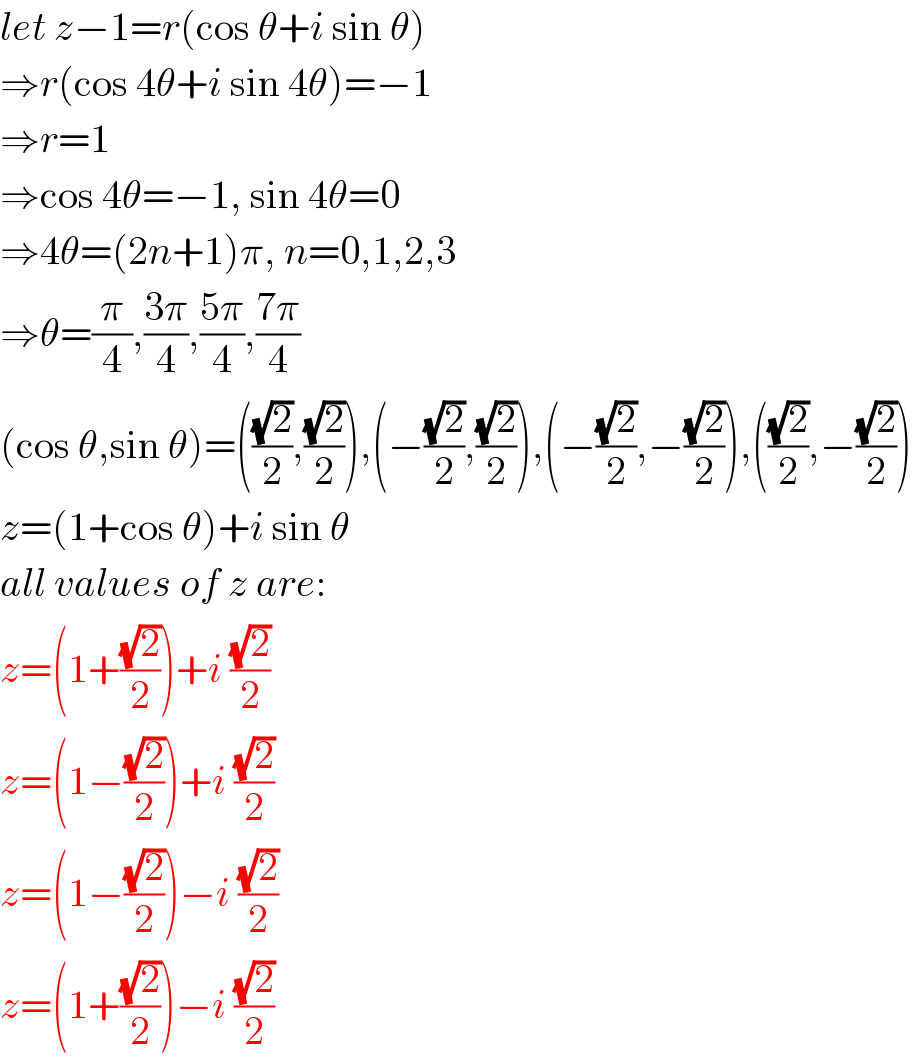
let z−1=r(cos θ+i sin θ) ⇒r(cos 4θ+i sin 4θ)=−1 ⇒r=1 ⇒cos 4θ=−1, sin 4θ=0 ⇒4θ=(2n+1)π, n=0,1,2,3 ⇒θ=(π/4),((3π)/4),((5π)/4),((7π)/4) (cos θ,sin θ)=(((√2)/2),((√2)/2)),(−((√2)/2),((√2)/2)),(−((√2)/2),−((√2)/2)),(((√2)/2),−((√2)/2)) z=(1+cos θ)+i sin θ all values of z are: z=(1+((√2)/2))+i ((√2)/2) z=(1−((√2)/2))+i ((√2)/2) z=(1−((√2)/2))−i ((√2)/2) z=(1+((√2)/2))−i ((√2)/2)

$${let}\:{z}−\mathrm{1}={r}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{r}\left(\mathrm{cos}\:\mathrm{4}\theta+{i}\:\mathrm{sin}\:\mathrm{4}\theta\right)=−\mathrm{1} \\ $$$$\Rightarrow{r}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{4}\theta=−\mathrm{1},\:\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\theta=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi,\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$$\left(\mathrm{cos}\:\theta,\mathrm{sin}\:\theta\right)=\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right),\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right),\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right),\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$${z}=\left(\mathrm{1}+\mathrm{cos}\:\theta\right)+{i}\:\mathrm{sin}\:\theta \\ $$$${all}\:{values}\:{of}\:{z}\:{are}: \\ $$$${z}=\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+{i}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${z}=\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+{i}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${z}=\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)−{i}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${z}=\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)−{i}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$

Commented by abdo.msup.com last updated on 23/Jun/18

let put z−1=x (e)⇔x^4 =e^(iπ) if x=r e^(iθ) we get r^4 e^(i4θ) =e^(i(2k+1)π) ⇒r=1 and 4θ=(2k+1)π ⇒θ_k =(((2k+1)π)/4) with k∈[[0,3]] and x_k =e^(i(((2k+1)π)/4)) ⇒z_k =x_k +1= 1+e^(i(((2k+1)π)/4)) ⇒ z_0 =1+e^(i(π/4)) z_1 =1+e^(i((3π)/4)) z_2 =1+e^(i((5π)/4)) z_3 =1+e^(i((7π)/4))

$${let}\:{put}\:{z}−\mathrm{1}={x}\:\:\left({e}\right)\Leftrightarrow{x}^{\mathrm{4}} \:={e}^{{i}\pi} \:\:{if}\:{x}={r}\:{e}^{{i}\theta} \\ $$$${we}\:{get}\:{r}^{\mathrm{4}} \:{e}^{{i}\mathrm{4}\theta} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow{r}=\mathrm{1}\:{and} \\ $$$$\mathrm{4}\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta_{{k}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}} \\ $$$${with}\:{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right]\:{and}\:{x}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}}} \\ $$$$\Rightarrow{z}_{{k}} ={x}_{{k}} \:+\mathrm{1}=\:\mathrm{1}+{e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}}} \:\:\Rightarrow \\ $$$${z}_{\mathrm{0}} =\mathrm{1}+{e}^{{i}\frac{\pi}{\mathrm{4}}} \\ $$$${z}_{\mathrm{1}} =\mathrm{1}+{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$${z}_{\mathrm{2}} =\mathrm{1}+{e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} \\ $$$${z}_{\mathrm{3}} =\mathrm{1}+{e}^{{i}\frac{\mathrm{7}\pi}{\mathrm{4}}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jun/18

z−1=(−1)^(1/4) cosΠ=−1 z−1={cos(2nΠ+Π)+isin(2nΠ+Π)}^(1/4) x+iy−1=cos(((2n+1)/4))+isin(((2n+1)/4)) (x−1)^2 +y^2 =cos^2 (((2n+1)/4))+sin^2 (((2n+1)/4)) (x−1)^2 +y^2 =1

$${z}−\mathrm{1}=\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${cos}\Pi=−\mathrm{1}\:\:\: \\ $$$${z}−\mathrm{1}=\left\{{cos}\left(\mathrm{2}{n}\Pi+\Pi\right)+{isin}\left(\mathrm{2}{n}\Pi+\Pi\right)\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${x}+{iy}−\mathrm{1}={cos}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right)+{isin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={cos}^{\mathrm{2}} \left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right)+{sin}^{\mathrm{2}} \left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com