
Question and Answers Forum
Question Number 38286 by mondodotto@gmail.com last updated on 23/Jun/18
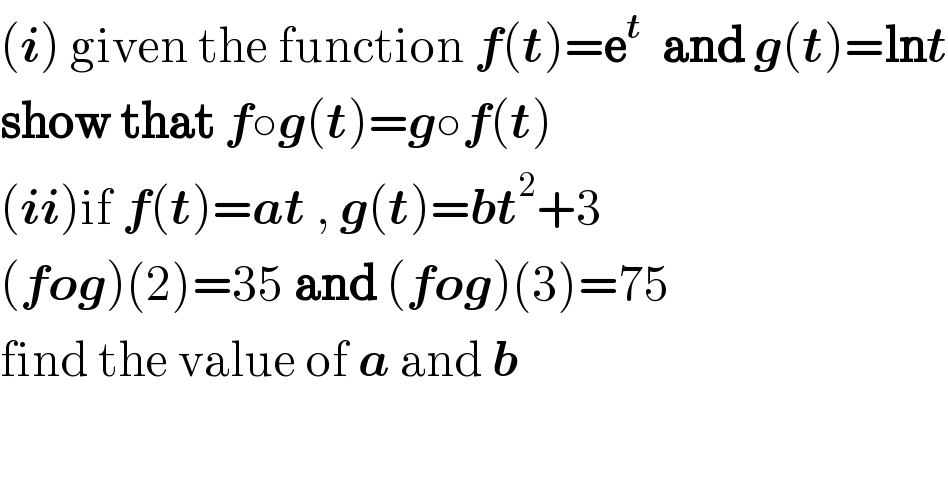
Commented by math khazana by abdo last updated on 24/Jun/18
![1) we have ∀t ∈R gof(t)=ln(e^t )=t ∀t∈]0,+∞[ fog(t)=e^(ln(t)) =t so we have fog=gof only on]0,+∞[ ! ii)fog(t)=f(g(t))=f(bt^2 +3)=a(bt^2 +3) fog(t)=f(g(t))=ag(t)=a(bt^2 +3) fog(2)=35⇒a(4b+3)=35 ⇒4ab +3a=35 fog(3)=75 ⇒a(9b +3)=75 ⇒9ab +3a=75 ⇒ 36ab +27 a= 9.35 and 36ab +12a=4.75 ⇒ 15a =9.35 −4.75⇒a = ((9.35)/(15)) −((4.75)/(15)) = ((3.3.5.7)/(3.5)) −((4.3.5.5)/(3.5)) =21 −20=1 ⇒ 4b=35−3=32 ⇒b=8 at this case f(t)=t and g(t)=8t^2 +3](Q38324.png)
| ||
Question and Answers Forum | ||
Question Number 38286 by mondodotto@gmail.com last updated on 23/Jun/18 | ||
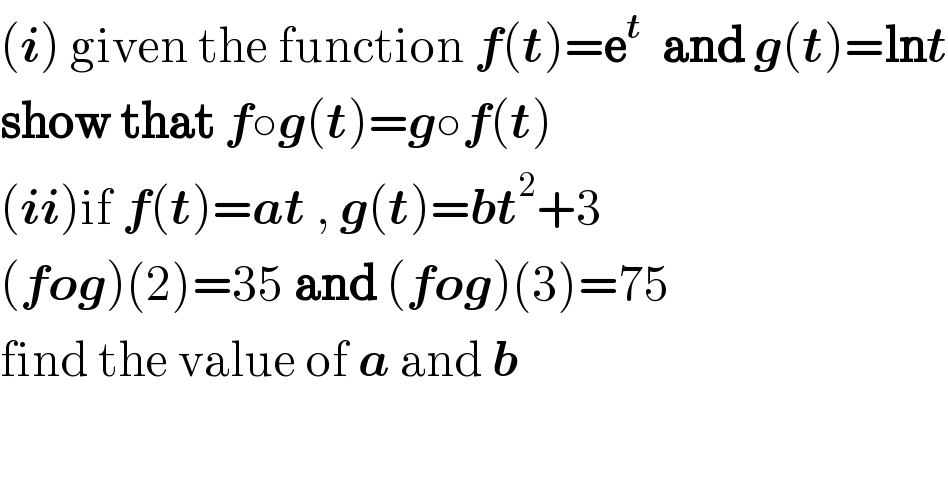 | ||
Commented by math khazana by abdo last updated on 24/Jun/18 | ||
![1) we have ∀t ∈R gof(t)=ln(e^t )=t ∀t∈]0,+∞[ fog(t)=e^(ln(t)) =t so we have fog=gof only on]0,+∞[ ! ii)fog(t)=f(g(t))=f(bt^2 +3)=a(bt^2 +3) fog(t)=f(g(t))=ag(t)=a(bt^2 +3) fog(2)=35⇒a(4b+3)=35 ⇒4ab +3a=35 fog(3)=75 ⇒a(9b +3)=75 ⇒9ab +3a=75 ⇒ 36ab +27 a= 9.35 and 36ab +12a=4.75 ⇒ 15a =9.35 −4.75⇒a = ((9.35)/(15)) −((4.75)/(15)) = ((3.3.5.7)/(3.5)) −((4.3.5.5)/(3.5)) =21 −20=1 ⇒ 4b=35−3=32 ⇒b=8 at this case f(t)=t and g(t)=8t^2 +3](Q38324.png) | ||