Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38397 by Fawomath last updated on 25/Jun/18

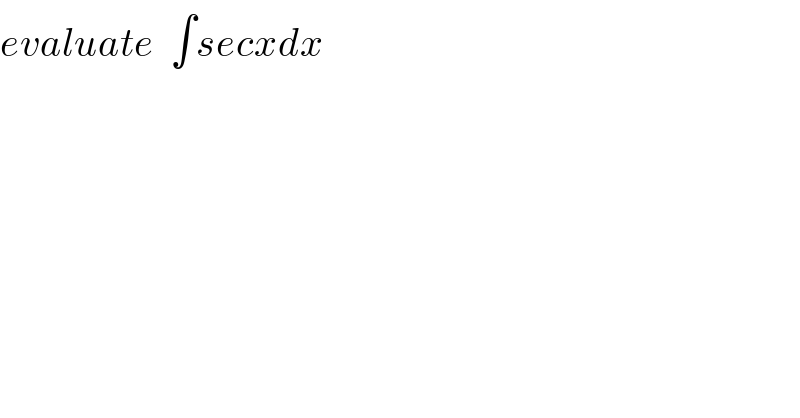
evaluate ∫secxdx

$${evaluate}\:\:\int{secxdx} \\ $$

Commented by maxmathsup by imad last updated on 25/Jun/18

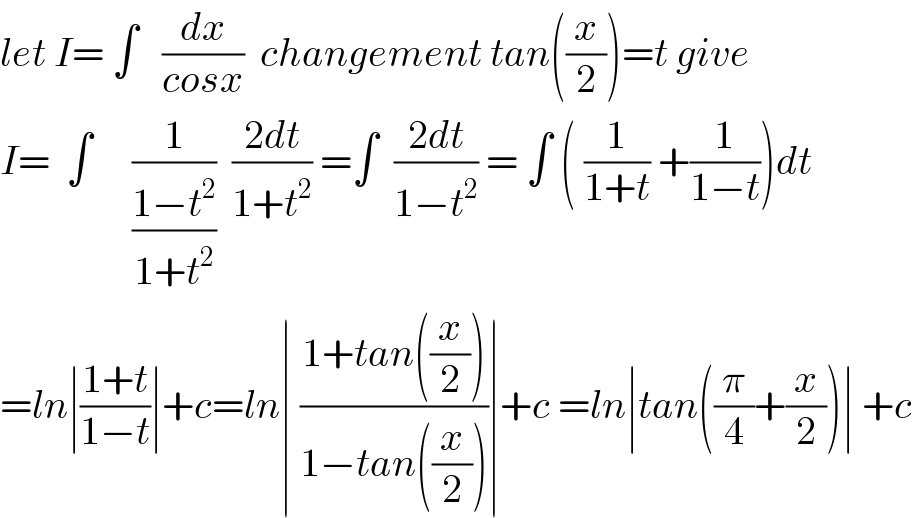
let I= ∫ (dx/(cosx)) changement tan((x/2))=t give I= ∫ (1/((1−t^2 )/(1+t^2 ))) ((2dt)/(1+t^2 )) =∫ ((2dt)/(1−t^2 )) = ∫ ( (1/(1+t)) +(1/(1−t)))dt =ln∣((1+t)/(1−t))∣+c=ln∣ ((1+tan((x/2)))/(1−tan((x/2))))∣+c =ln∣tan((π/4)+(x/2))∣ +c

$${let}\:{I}=\:\int\:\:\:\frac{{dx}}{{cosx}}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}=\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\:\int\:\left(\:\frac{\mathrm{1}}{\mathrm{1}+{t}}\:+\frac{\mathrm{1}}{\mathrm{1}−{t}}\right){dt} \\ $$$$={ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid+{c}={ln}\mid\:\frac{\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\mid+{c}\:={ln}\mid{tan}\left(\frac{\pi}{\mathrm{4}}+\frac{{x}}{\mathrm{2}}\right)\mid\:+{c} \\ $$

Commented by Cheyboy last updated on 25/Jun/18

∫ secx dx ∫ (secx .((secx+tanx)/(secx+tanx)))dx ∫ (((sec^2 x+secxtanx)/(secx+tanx))) dx let u=secx+tanx du=(secxtanx+sec^2 x)dx ∫(1/u) du ln∣u∣ +C ln ∣secx+tanx∣+C

$$\int\:\boldsymbol{{secx}}\:\boldsymbol{{dx}} \\ $$$$\int\:\left(\boldsymbol{{secx}}\:.\frac{\boldsymbol{{secx}}+\boldsymbol{{tanx}}}{\boldsymbol{{secx}}+\boldsymbol{{tanx}}}\right)\boldsymbol{{dx}} \\ $$$$\int\:\left(\frac{\boldsymbol{{sec}}^{\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{secxtanx}}}{\boldsymbol{{secx}}+\boldsymbol{{tanx}}}\right)\:\boldsymbol{{dx}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{u}}=\boldsymbol{{secx}}+\boldsymbol{{tanx}} \\ $$$$\boldsymbol{{du}}=\left(\boldsymbol{{secxtanx}}+\boldsymbol{{sec}}^{\mathrm{2}} \boldsymbol{{x}}\right)\boldsymbol{{dx}} \\ $$$$\int\frac{\mathrm{1}}{\boldsymbol{{u}}}\:\boldsymbol{{du}} \\ $$$$\mathrm{ln}\mid\boldsymbol{{u}}\mid\:+{C} \\ $$$$\mathrm{ln}\:\mid\boldsymbol{{secx}}+\boldsymbol{{tanx}}\mid+{C} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18

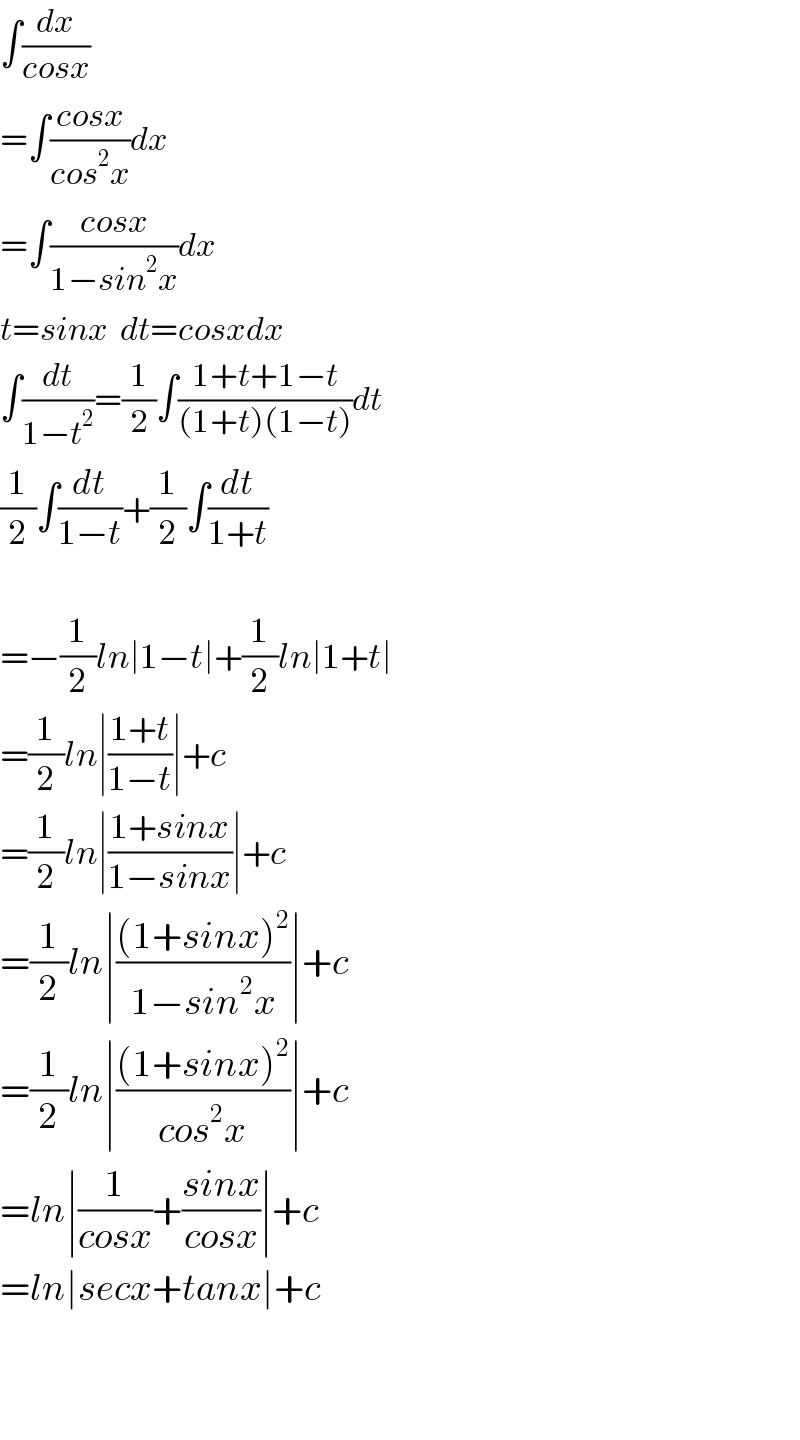
∫(dx/(cosx)) =∫((cosx)/(cos^2 x))dx =∫((cosx)/(1−sin^2 x))dx t=sinx dt=cosxdx ∫(dt/(1−t^2 ))=(1/2)∫((1+t+1−t)/((1+t)(1−t)))dt (1/2)∫(dt/(1−t))+(1/2)∫(dt/(1+t)) =−(1/2)ln∣1−t∣+(1/2)ln∣1+t∣ =(1/2)ln∣((1+t)/(1−t))∣+c =(1/2)ln∣((1+sinx)/(1−sinx))∣+c =(1/2)ln∣(((1+sinx)^2 )/(1−sin^2 x))∣+c =(1/2)ln∣(((1+sinx)^2 )/(cos^2 x))∣+c =ln∣(1/(cosx))+((sinx)/(cosx))∣+c =ln∣secx+tanx∣+c

$$\int\frac{{dx}}{{cosx}} \\ $$$$=\int\frac{{cosx}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{{cosx}}{\mathrm{1}−{sin}^{\mathrm{2}} {x}}{dx} \\ $$$${t}={sinx}\:\:{dt}={cosxdx} \\ $$$$\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{t}+\mathrm{1}−{t}}{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}\right)}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{1}+{t}} \\ $$$$ \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{t}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{t}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{sinx}}{\mathrm{1}−{sinx}}\mid+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\left(\mathrm{1}+{sinx}\right)^{\mathrm{2}} }{\mathrm{1}−{sin}^{\mathrm{2}} {x}}\mid+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\left(\mathrm{1}+{sinx}\right)^{\mathrm{2}} }{{cos}^{\mathrm{2}} {x}}\mid+{c} \\ $$$$={ln}\mid\frac{\mathrm{1}}{{cosx}}+\frac{{sinx}}{{cosx}}\mid+{c} \\ $$$$={ln}\mid{secx}+{tanx}\mid+{c} \\ $$$$ \\ $$$$ \\ $$

Answered by malwaan last updated on 25/Jun/18

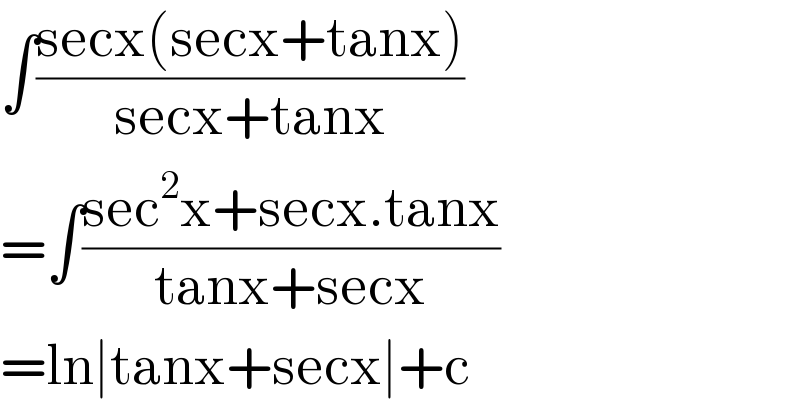
∫((secx(secx+tanx))/(secx+tanx)) =∫((sec^2 x+secx.tanx)/(tanx+secx)) =ln∣tanx+secx∣+c

$$\int\frac{\mathrm{secx}\left(\mathrm{secx}+\mathrm{tanx}\right)}{\mathrm{secx}+\mathrm{tanx}} \\ $$$$=\int\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{secx}.\mathrm{tanx}}{\mathrm{tanx}+\mathrm{secx}} \\ $$$$=\mathrm{ln}\mid\mathrm{tanx}+\mathrm{secx}\mid+\mathrm{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com