Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 38495 by kunal1234523 last updated on 26/Jun/18

prove that tan 3a tan 2a tan a = tan 3a − tan 2a − tan a

$${prove}\:{that} \\ $$$$\boldsymbol{\mathrm{tan}}\:\mathrm{3}\boldsymbol{{a}}\:\boldsymbol{\mathrm{tan}}\:\mathrm{2}\boldsymbol{{a}}\:\boldsymbol{\mathrm{tan}}\:\boldsymbol{{a}}\:=\:\:\boldsymbol{\mathrm{tan}}\:\mathrm{3}\boldsymbol{{a}}\:−\:\boldsymbol{\mathrm{tan}}\:\mathrm{2}\boldsymbol{{a}}\:−\:\boldsymbol{\mathrm{tan}}\:\boldsymbol{{a}} \\ $$

Answered by kunal1234523 last updated on 26/Jun/18

tan 3a = tan (a+2a) ⇒tan 3a = ((tan a + tan 2a)/(1 − tan a tan 2a)) ⇒tan 3a − tan a tan 2a tan 3a = tan a + tan 2a ⇒tan 3a tan 2a tan a = tan 3a − tan 2a −tan a

$${tan}\:\mathrm{3}{a}\:=\:{tan}\:\left({a}+\mathrm{2}{a}\right) \\ $$$$\Rightarrow{tan}\:\mathrm{3}{a}\:=\:\frac{{tan}\:{a}\:+\:{tan}\:\mathrm{2}{a}}{\mathrm{1}\:−\:{tan}\:{a}\:{tan}\:\mathrm{2}{a}} \\ $$$$\Rightarrow{tan}\:\mathrm{3}{a}\:−\:{tan}\:{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:\mathrm{3}{a}\:=\:{tan}\:{a}\:+\:{tan}\:\mathrm{2}{a} \\ $$$$\Rightarrow{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:{a}\:=\:{tan}\:\mathrm{3}{a}\:−\:{tan}\:\mathrm{2}{a}\:−{tan}\:{a} \\ $$

Answered by kunal1234523 last updated on 26/Jun/18

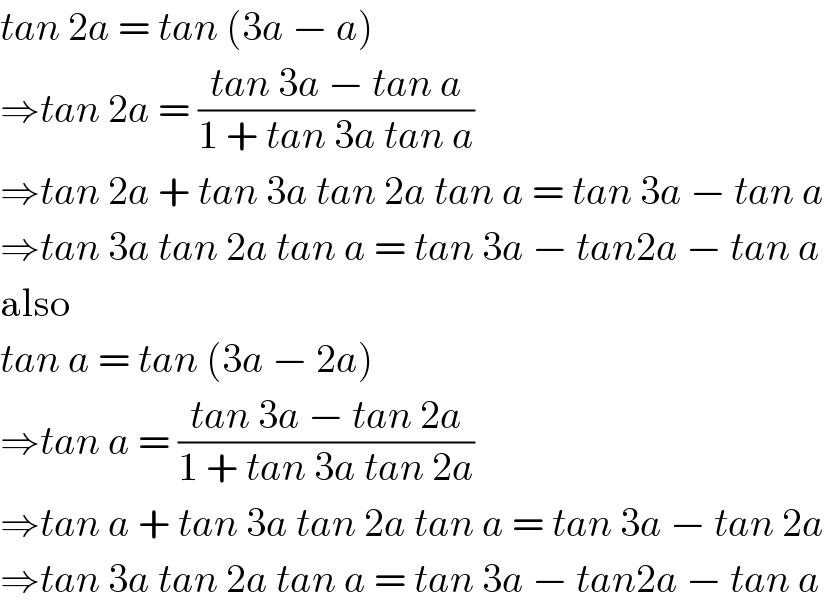
tan 2a = tan (3a − a) ⇒tan 2a = ((tan 3a − tan a)/(1 + tan 3a tan a)) ⇒tan 2a + tan 3a tan 2a tan a = tan 3a − tan a ⇒tan 3a tan 2a tan a = tan 3a − tan2a − tan a also tan a = tan (3a − 2a) ⇒tan a = ((tan 3a − tan 2a)/(1 + tan 3a tan 2a)) ⇒tan a + tan 3a tan 2a tan a = tan 3a − tan 2a ⇒tan 3a tan 2a tan a = tan 3a − tan2a − tan a

$${tan}\:\mathrm{2}{a}\:=\:{tan}\:\left(\mathrm{3}{a}\:−\:{a}\right) \\ $$$$\Rightarrow{tan}\:\mathrm{2}{a}\:=\:\frac{{tan}\:\mathrm{3}{a}\:−\:{tan}\:{a}}{\mathrm{1}\:+\:{tan}\:\mathrm{3}{a}\:{tan}\:{a}} \\ $$$$\Rightarrow{tan}\:\mathrm{2}{a}\:+\:{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:{a}\:=\:{tan}\:\mathrm{3}{a}\:−\:{tan}\:{a} \\ $$$$\Rightarrow{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:{a}\:=\:{tan}\:\mathrm{3}{a}\:−\:{tan}\mathrm{2}{a}\:−\:{tan}\:{a} \\ $$$$\mathrm{also} \\ $$$${tan}\:{a}\:=\:{tan}\:\left(\mathrm{3}{a}\:−\:\mathrm{2}{a}\right) \\ $$$$\Rightarrow{tan}\:{a}\:=\:\frac{{tan}\:\mathrm{3}{a}\:−\:{tan}\:\mathrm{2}{a}}{\mathrm{1}\:+\:{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}} \\ $$$$\Rightarrow{tan}\:{a}\:+\:{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:{a}\:=\:{tan}\:\mathrm{3}{a}\:−\:{tan}\:\mathrm{2}{a} \\ $$$$\Rightarrow{tan}\:\mathrm{3}{a}\:{tan}\:\mathrm{2}{a}\:{tan}\:{a}\:=\:{tan}\:\mathrm{3}{a}\:−\:{tan}\mathrm{2}{a}\:−\:{tan}\:{a} \\ $$

Answered by kunal1234523 last updated on 26/Jun/18

but there should be one more apporach and I am stucked there LHS ((sin 3a sin 2a sin a)/(cos 3a cos 2a cos a)) =((sin 3a (cos a − cos 3a))/(2 cos 3a cos 2a cos a)) =((sin 3a cos a)/(2cos 3a cos 2a cos a)) − ((sin 3a cos3a)/(2 cos 3a cos 2a cos a)) =((tan 3a)/(2 cos 2a)) − ((sin(a + 2a))/(2 cos a cos 2a)) =((tan 3a)/(2 cos 2a)) − (((sin a cos 2a)/(2 cos a cos 2a)) + ((cos a sin 2a)/(2 cos a cos 2a))) =((tan 3a)/(2 cos 2a))− ((tan 2a)/2) − ((tan a)/2) =(1/2)[((tan 3a)/(cos 2a)) − tan 2a − tan a] now what should I do.....

$${but}\:{there}\:{should}\:{be}\:{one}\:{more}\:{apporach}\:{and}\: \\ $$$${I}\:{am}\:{stucked}\:{there} \\ $$$${LHS} \\ $$$$\frac{{sin}\:\mathrm{3}{a}\:{sin}\:\mathrm{2}{a}\:{sin}\:{a}}{{cos}\:\mathrm{3}{a}\:{cos}\:\mathrm{2}{a}\:{cos}\:{a}}\: \\ $$$$=\frac{{sin}\:\mathrm{3}{a}\:\left({cos}\:{a}\:−\:{cos}\:\mathrm{3}{a}\right)}{\mathrm{2}\:{cos}\:\mathrm{3}{a}\:{cos}\:\mathrm{2}{a}\:{cos}\:{a}} \\ $$$$=\frac{{sin}\:\mathrm{3}{a}\:{cos}\:{a}}{\mathrm{2}{cos}\:\mathrm{3}{a}\:{cos}\:\mathrm{2}{a}\:{cos}\:{a}}\:−\:\frac{{sin}\:\mathrm{3}{a}\:{cos}\mathrm{3}{a}}{\mathrm{2}\:{cos}\:\mathrm{3}{a}\:{cos}\:\mathrm{2}{a}\:{cos}\:{a}} \\ $$$$=\frac{{tan}\:\mathrm{3}{a}}{\mathrm{2}\:{cos}\:\mathrm{2}{a}}\:−\:\frac{{sin}\left({a}\:+\:\mathrm{2}{a}\right)}{\mathrm{2}\:{cos}\:{a}\:{cos}\:\mathrm{2}{a}} \\ $$$$=\frac{{tan}\:\mathrm{3}{a}}{\mathrm{2}\:{cos}\:\mathrm{2}{a}}\:−\:\left(\frac{{sin}\:{a}\:{cos}\:\mathrm{2}{a}}{\mathrm{2}\:{cos}\:{a}\:{cos}\:\mathrm{2}{a}}\:+\:\frac{{cos}\:{a}\:{sin}\:\mathrm{2}{a}}{\mathrm{2}\:{cos}\:{a}\:{cos}\:\mathrm{2}{a}}\right) \\ $$$$=\frac{{tan}\:\mathrm{3}{a}}{\mathrm{2}\:{cos}\:\mathrm{2}{a}}−\:\frac{{tan}\:\mathrm{2}{a}}{\mathrm{2}}\:−\:\frac{{tan}\:{a}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{tan}\:\mathrm{3}{a}}{{cos}\:\mathrm{2}{a}}\:−\:{tan}\:\mathrm{2}{a}\:−\:{tan}\:{a}\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{what}}\:\boldsymbol{{should}}\:\boldsymbol{{I}}\:\boldsymbol{{do}}..... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jun/18

scanning it meticulously...give time ...

$${scanning}\:{it}\:{meticulously}...{give}\:{time}\:... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jun/18

((tan3a)/(2cos2a))−((tan2a)/2)−((tana)/2) tan3a−tan2a−tana+((tan3a)/(2cos2a))−tan3a+tan2a −((tan2a)/2)+tana−((tana)/2) tan3a−tan2a−tana+tan3a((1/(2cos2a))−1)+(1/2) (tan2a+tana) do+tan3a((1/(2cos2a))−1)+(1/2)(((sin3a)/(cos2acosa))) =do+((sin3a)/(2cos3acos2a))−((sin3a)/(cos3a))+((sin3a)/(2cos2acosa)) do+sin3a((1/(2cos3acos2a))−(1/(cos3a))+(1/(2cos2acosa))) do+sin3a(((cosa+cos3a)/(2cos3acos2acosa))−(1/(cos3a))) do+sin3a(((2cos2a.cosa)/(2cos3acos2acosa))−(1/(cos3a))) do+sin3a((1/(cos3a))−(1/(cos3a))) =do +0 =tan3a−tan2a−tana proved

$$\frac{{tan}\mathrm{3}{a}}{\mathrm{2}{cos}\mathrm{2}{a}}−\frac{{tan}\mathrm{2}{a}}{\mathrm{2}}−\frac{{tana}}{\mathrm{2}} \\ $$$${tan}\mathrm{3}{a}−{tan}\mathrm{2}{a}−{tana}+\frac{{tan}\mathrm{3}{a}}{\mathrm{2}{cos}\mathrm{2}{a}}−{tan}\mathrm{3}{a}+{tan}\mathrm{2}{a} \\ $$$$−\frac{{tan}\mathrm{2}{a}}{\mathrm{2}}+{tana}−\frac{{tana}}{\mathrm{2}} \\ $$$${tan}\mathrm{3}{a}−{tan}\mathrm{2}{a}−{tana}+{tan}\mathrm{3}{a}\left(\frac{\mathrm{1}}{\mathrm{2}{cos}\mathrm{2}{a}}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({tan}\mathrm{2}{a}+{tana}\right) \\ $$$${do}+{tan}\mathrm{3}{a}\left(\frac{\mathrm{1}}{\mathrm{2}{cos}\mathrm{2}{a}}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{sin}\mathrm{3}{a}}{{cos}\mathrm{2}{acosa}}\right) \\ $$$$={do}+\frac{{sin}\mathrm{3}{a}}{\mathrm{2}{cos}\mathrm{3}{acos}\mathrm{2}{a}}−\frac{{sin}\mathrm{3}{a}}{{cos}\mathrm{3}{a}}+\frac{{sin}\mathrm{3}{a}}{\mathrm{2}{cos}\mathrm{2}{acosa}} \\ $$$${do}+{sin}\mathrm{3}{a}\left(\frac{\mathrm{1}}{\mathrm{2}{cos}\mathrm{3}{acos}\mathrm{2}{a}}−\frac{\mathrm{1}}{{cos}\mathrm{3}{a}}+\frac{\mathrm{1}}{\mathrm{2}{cos}\mathrm{2}{acosa}}\right) \\ $$$${do}+{sin}\mathrm{3}{a}\left(\frac{{cosa}+{cos}\mathrm{3}{a}}{\mathrm{2}{cos}\mathrm{3}{acos}\mathrm{2}{acosa}}−\frac{\mathrm{1}}{{cos}\mathrm{3}{a}}\right) \\ $$$${do}+{sin}\mathrm{3}{a}\left(\frac{\mathrm{2}{cos}\mathrm{2}{a}.{cosa}}{\mathrm{2}{cos}\mathrm{3}{acos}\mathrm{2}{acosa}}−\frac{\mathrm{1}}{{cos}\mathrm{3}{a}}\right) \\ $$$${do}+{sin}\mathrm{3}{a}\left(\frac{\mathrm{1}}{{cos}\mathrm{3}{a}}−\frac{\mathrm{1}}{{cos}\mathrm{3}{a}}\right) \\ $$$$={do}\:\:+\mathrm{0} \\ $$$$={tan}\mathrm{3}{a}−{tan}\mathrm{2}{a}−{tana}\:{proved} \\ $$$$ \\ $$$$ \\ $$

Commented by kunal1234523 last updated on 27/Jun/18

wow you take a “do” then proved everything else is zero smart.

$${wow}\:{you}\:{take}\:{a}\:``{do}''\:{then}\:{proved}\:{everything} \\ $$$${else}\:{is}\:{zero}\:{smart}. \\ $$

Answered by MJS last updated on 26/Jun/18

1=((tan 3α −tan 2α −tan α)/(tan 3α tan 2α tan α)) 1=(1/(tan 2α tan α))−(1/(tan 3α tan α))−(1/(tan 3α tan 2α)) α=arctan t 1=(1/(((2t)/(1−t^2 ))×t))−(1/(((3t−t^3 )/(3t^2 −1))×t))−(1/(((2t)/(1−t^2 ))×((3t−t^3 )/(3t^2 −1)))) 1=((1−t^2 )/(2t^2 ))−((3t^2 −1)/(t^2 (t^2 −3)))−(((1−t^2 )(3t^2 −1))/(2t^2 (t^2 −3))) 1=(((1−t^2 )(t^2 −3)−2(3t^2 −1)−(1−t^2 )(3t^2 −1))/(2t^2 (t^2 −3))) 1=(((1−t^2 )(t^2 −3)−(3t^2 −1)(2+1−t^2 ))/(2t^2 (t^2 −3))) 1=(((1−t^2 )(t^2 −3)−(3t^2 −1)(3−t^2 ))/(2t^2 (t^2 −3))) 1=(((t^2 −3)((1−t^2 )+(3t^2 −1)))/(2t^2 (t^2 −3))) 1=(((t^2 −3)2t^2 )/(2t^2 (t^2 −3))) 1=1 proved

$$ \\ $$$$\mathrm{1}=\frac{\mathrm{tan}\:\mathrm{3}\alpha\:−\mathrm{tan}\:\mathrm{2}\alpha\:−\mathrm{tan}\:\alpha}{\mathrm{tan}\:\mathrm{3}\alpha\:\mathrm{tan}\:\mathrm{2}\alpha\:\mathrm{tan}\:\alpha} \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}\alpha\:\mathrm{tan}\:\alpha}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{3}\alpha\:\mathrm{tan}\:\alpha}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{3}\alpha\:\mathrm{tan}\:\mathrm{2}\alpha} \\ $$$$\alpha=\mathrm{arctan}\:{t} \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }×{t}}−\frac{\mathrm{1}}{\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}×{t}}−\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }×\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\mathrm{1}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}^{\mathrm{2}} }−\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)}−\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{2}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{3}\right)−\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}+\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{3}\right)−\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\frac{\left({t}^{\mathrm{2}} −\mathrm{3}\right)\left(\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)\right)}{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\frac{\left({t}^{\mathrm{2}} −\mathrm{3}\right)\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\mathrm{1}=\mathrm{1}\:\mathrm{proved} \\ $$

Commented by kunal1234523 last updated on 27/Jun/18

really simple and cool. there you had been taken t = tan α , i think

$${really}\:{simple}\:{and}\:{cool}.\:{there}\:{you}\:{had}\:{been}\: \\ $$$${taken}\:{t}\:=\:{tan}\:\alpha\:,\:{i}\:{think} \\ $$

Commented by MJS last updated on 27/Jun/18

yes.

$$\mathrm{yes}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com