
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 38643 by maxmathsup by imad last updated on 27/Jun/18
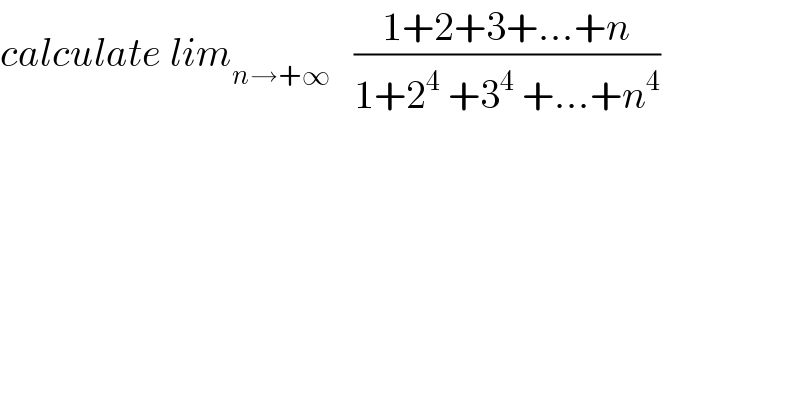
Commented by abdo mathsup 649 cc last updated on 28/Jun/18
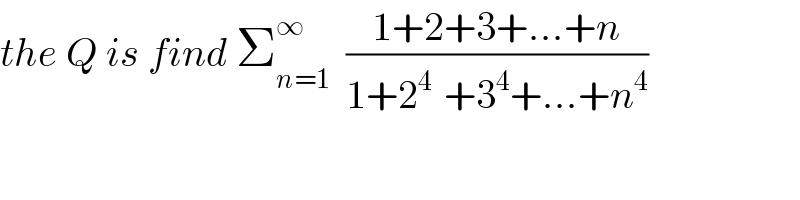
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18
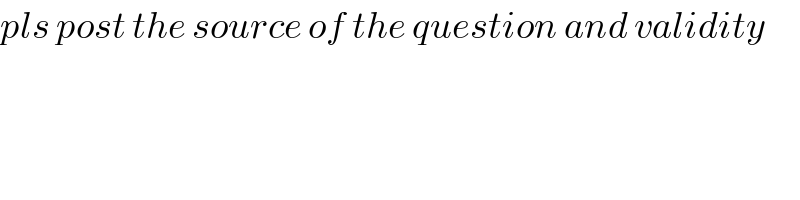
Answered by ajfour last updated on 28/Jun/18
![Σ_(r=1) ^n r^4 = Σ_(r=1) ^n r(r+1)(r+2)(r+3) −6Σ_(r=1) ^n r^3 −11Σ_(r=1) ^n r^2 −6Σ_(r=1) ^n r =((n(n+1)(n+2)(n+3)(n+4))/5) −((6n^2 (n+1)^2 )/4)−((11n(n+1)(2n+1))/6) −((6n(n+1))/2) = ((n(n+1))/(30)){6(n+2)(n+3)(n+4) −45n(n+1)−55(2n+1)−90} =((n(n+1))/(30)){6n^3 +9n^2 +6n−1} So lim_(n→∞) (((Σ_(r=1) ^n r)^(5/2) )/(Σ_(r=1) ^n r^4 )) = lim_(n→∞) (([((n(n+1))/2)]^(5/2) )/([((n(n+1))/(30))(6n^3 +9n^2 +6n−1)])) =((((1/2))^(5/2) )/(((1/(30)))×6)) = (5/(4(√2))) .](Q38652.png)
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

Commented by ajfour last updated on 28/Jun/18

