Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 38699 by Tinkutara last updated on 28/Jun/18

Answered by behi83417@gmail.com last updated on 28/Jun/18

y^2 =a^2 +b^2 +2(√((a^2 cos^2 x+b^2 sin^2 x)(a^2 sin^2 x+b^2 cos^2 x))) P=a^2 cos^2 x+b^2 sin^2 x,Q=a^2 sin^2 x+b^2 cos^2 x P+Q=const,PQ,will be max,when: P=Q ⇒a^2 cos^2 x+b^2 sin^2 x=a^2 sin^2 x+b^2 cos^2 x ⇒a^2 cos2x=b^2 cos2x⇒a=b(×) ∨cos2x=0 ⇒y^2 ≤a^2 +b^2 +2(√(((a^2 +b^2 )/2).((a^2 +b^2 )/2)))=2(a^2 +b^2 ) ⇒0<y≤(√(2(a^2 +b^2 ))) .■

$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\right)} \\ $$$${P}={a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x},{Q}={a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x} \\ $$$${P}+{Q}={const},{PQ},{will}\:{be}\:{max},{when}:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{P}={Q} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}={a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {cos}\mathrm{2}{x}={b}^{\mathrm{2}} {cos}\mathrm{2}{x}\Rightarrow\boldsymbol{{a}}=\boldsymbol{{b}}\left(×\right)\:\vee{cos}\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}.\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}}=\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{0}<{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\:\:.\blacksquare \\ $$

Commented by behi83417@gmail.com last updated on 28/Jun/18

dear master:mrW3! thank you so much for solving Q#38032. no message recive to mi from app.so i don't see your answer on this Q.anyway thanks.

Commented by MrW3 last updated on 29/Jun/18

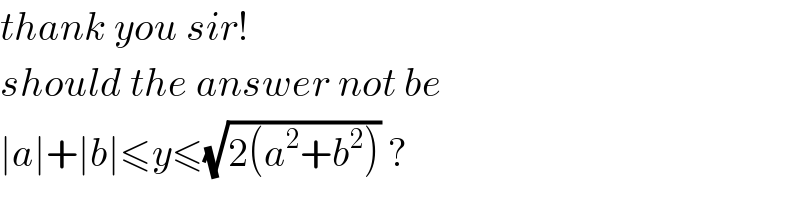
thank you sir! should the answer not be ∣a∣+∣b∣≤y≤(√(2(a^2 +b^2 ))) ?

$${thank}\:{you}\:{sir}! \\ $$$${should}\:{the}\:{answer}\:{not}\:{be} \\ $$$$\mid{a}\mid+\mid{b}\mid\leqslant{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\:? \\ $$

Commented by behi83417@gmail.com last updated on 28/Jun/18

way not! please confirm.

$${way}\:{not}!\:{please}\:{confirm}. \\ $$

Commented by MrW3 last updated on 29/Jun/18

y^2 =a^2 +b^2 +2(√((a^2 cos^2 x+b^2 sin^2 x)(a^2 sin^2 x+b^2 cos^2 x))) y^2 =a^2 +b^2 +2(√((a^4 sin^2 xcos^2 x+a^2 b^2 sin^4 x+a^2 b^2 cos^4 x+b^4 sin^2 xcos^2 x)) y^2 =a^2 +b^2 +2(√((a^4 +b^4 )sin^2 xcos^2 x+a^2 b^2 (sin^4 x+cos^4 x))) y^2 =a^2 +b^2 +2(√((a^4 +b^4 )sin^2 xcos^2 x+a^2 b^2 (sin^4 x+cos^4 x+2sin^2 xcos^2 x)−2a^2 b^2 sin^2 xcos^2 x)) y^2 =a^2 +b^2 +2(√((a^4 +b^4 −2a^2 b^2 )sin^2 xcos^2 x+a^2 b^2 (sin^2 x+cos^2 x)^2 )) y^2 =a^2 +b^2 +2(√((a^2 −b^2 )^2 sin^2 xcos^2 x+a^2 b^2 )) y^2 =a^2 +b^2 +2(√((1/4)(a^2 −b^2 )^2 sin^2 2x+a^2 b^2 )) y^2 =a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 sin^2 2x)) ⇒y=(√(a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 sin^2 2x)))) min. y at sin 2x=0: y_(min) =(√(a^2 +b^2 +(√(4a^2 b^2 )))) =(√(a^2 +b^2 +2∣a∣∣b∣))=∣a∣+∣b∣ max. y at sin 2x=±1: y_(max) =(√(a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 )))) =(√(a^2 +b^2 +(√((a^2 +b^2 )^2 )))) =(√(2(a^2 +b^2 ))) ⇒∣a∣+∣b∣≤y≤(√(2(a^2 +b^2 )))

$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\right)} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} \mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {sin}^{\mathrm{4}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {cos}^{\mathrm{4}} {x}+{b}^{\mathrm{4}} \mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}\right.} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}\right)} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}+\mathrm{2sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}\right)−\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}} \\ $$$$\Rightarrow{y}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}} \\ $$$${min}.\:{y}\:{at}\:\mathrm{sin}\:\mathrm{2}{x}=\mathrm{0}: \\ $$$${y}_{{min}} =\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}\:=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\mid{a}\mid\mid{b}\mid}=\mid{a}\mid+\mid{b}\mid \\ $$$${max}.\:{y}\:{at}\:\mathrm{sin}\:\mathrm{2}{x}=\pm\mathrm{1}: \\ $$$${y}_{{max}} =\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\Rightarrow\mid{a}\mid+\mid{b}\mid\leqslant{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$

Commented by behi83417@gmail.com last updated on 29/Jun/18

perfect!

$${perfect}! \\ $$

Commented by Tinkutara last updated on 29/Jun/18

Ans given is [(a+b),(√(2(a^2 +b^2 )))]

$${Ans}\:{given}\:{is}\:\left[\left({a}+{b}\right),\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\right] \\ $$

Commented by Tinkutara last updated on 29/Jun/18

Thank you very much Sir! I got the answer. ��������

Terms of Service

Privacy Policy

Contact: info@tinkutara.com